Archivi tag: tempo
CONCETTO DI TEMPO: Post aperto a vari interventi (dott. prof. Marco Rosa-Clot, dott. Piero Pistoia, dott. ing. Michele Franchi ….,post aperto
Curriculum di piero pistoia:
piero-pistoia-curriculumok (#)
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
L’argomento proposto, da trattare da più punti di vista (scientifico, filosofico, epistemologico, matematico ecc.) oltre al fascino che emana non trascurabile in situazioni di apprendimento, toccando alcune strutture nevralgiche della conoscenza scientifica attuale, è ricco di riferimenti, sottigliezze ed implicazioni anche per la programmazione curricolare, portando all’attenzione degli insegnanti spunti focali di riflessione e discussione (anche sul metodo) nell’ambito delle discipline scientifiche e filosofiche.
LA GRAVITA’, LA TERMODINAMICA ED IL TEMPO
PUO’ L’ORDINE NASCERE DAL CASO?
Chi ha paura del II Principio della Termodinamica?
Dott. Prof. Marco Rosa-Clot
(Professore ordinario di Fisica, Università di Firenze)
SE VUOI LEGGERE L’ARTICOLO DI MARCO ROSA-CLOT CLICCA SU: RosaClot_tempo
PER VEDERE IL CURRICULUM DI ROSA-CLOT CLICCARE SU:
_________________________________________________________
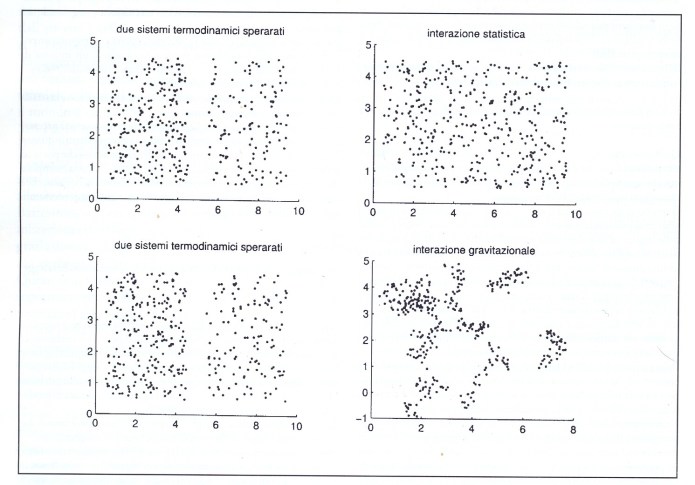
ATTENZIONE! I lettori curiosi, meravigliati da questi articoli, sono in attesa di ricevere (come promesso) da parte del prof. Rosa-Clot informazioni sul programma che permetta di veder girare su tutti i personal computers una simulazione in cui nubi di gas e particelle, pur isolate, evolvono <clusterizzando> (Fig.1)!? I PROMOTORI DEL BLOG
———————————————————————————————
LA FRECCIA DEL TEMPO
Uno dei concetti più densi coglibili nel divenire delle cose
del dott. Piero Pistoia
Versione rivisitata da: ‘Didattica delle scienze’ n.220. Maggio 2002; ‘Didattica delle Scienze’ n.221. Ottobre 2002 e da ‘Il Sillabario’ n.2, 1998.
PER VISIONARE L’ARTICOLO: cliccare su FRECCIA DEL TEMPO2
CURRICULUM DI PIERO PISTOIA CLICCARE SU:
.
______________________________________
SEGUONO DUE BANALI ROUTINES (a: nt=60, n=300 e b: nt=6, n=30) DA COPIARE SULLA CONSOLLE DEL LINGUAGGIO R PER TRACCIARE I CORRISPETTIVI GRAFICI RELATIVI ALLA FRECCIA DEL TEMPO di Piero Pistoia
PRIMA ROUTINE BOZZA
nt=60 # numero molecole nel box di sinistra al tempo zero
n=300 # numero dei passaggi
nc=runif(n, min=0, max=1) # n numeri pseudo-casuali compresi fra 0 e 1
ns=c()
ns=ns[1:n]=0 # azzero gli elementi del vettore ns che registrerà il numero delle presenze nel box di sinistra
ns[1]=nt
for(i in 1:(n-1)){ n1=ns[i]-1/nt # inizia l’algoritmo di MERSENNE TWISTER
if(nc[i]<=n1) ns[i+1]=ns[i]-1 else ns[i+1]=ns[i]+1
}
plot(ns)
PRIMA ROUTINE DEFINITIVA
#COPIA SULLA CONSOLLE DI R
library(graphics)
nt=60
n=300
nc=runif(n,min=0,max=1)
ns=c()
ns=ns[1:nt]=0
ns[1]=nt
for(i in 1:(n-1)){n1=ns[i]/nt
if(nc[i]<=n1) ns[i+1]=ns[i]-1 else ns[i+1]=ns[i]+1
}
x=c(1:n)
par(ask=T)
plot(x,ns,type='l')
# elimino ora circa il 10% degli elementi iniziali che falsano la media e gli errori
# calcolo poi gli errori
v=n/10
ns1=ns[v:n]
x1=x[v:n]
plot(x,ns,type='l',xlim=c(v,n), ylim=c(1,nt))
media_ns1=sum(ns1)/n
media_ns1
errqm_ns1=sqrt(sum((media_ns1-ns1)^2)/n)
errqm_ns1
errel_ns1=errqm_ns1/media_ns1
errel_ns1
# FINE COPIA
RISULTATI DELLA PRIMA ROUTINE
> rm(list=ls(all=TRUE))
> library(graphics)
>
> nt=60
> n=300
> nc=runif(n,min=0,max=1)
> ns=c()
> ns=ns[1:nt]=0
> ns[1]=nt
> for(i in 1:(n-1)){n1=ns[i]/nt
+ if(nc[i]<=n1) ns[i+1]=ns[i]-1 else ns[i+1]=ns[i]+1
+ }
> x=c(1:n)
> par(ask=T)
> plot(x,ns,type='l')
Aspetto per confermare cambio pagina...
>
> # elimino ora circa il 10% degli elementi iniziali che falsano la media e gli errori
> # calcolo poi gli errori
> v=n/10
>
> ns1=ns[v:n]
> x1=x[v:n]
> plot(x,ns,type='l',xlim=c(v,n), ylim=c(1,nt))
Aspetto per confermare cambio pagina...
>
> media_ns1=sum(ns1)/n
> media_ns1
[1] 29.29333
> errqm_ns1=sqrt(sum((media_ns1-ns1)^2)/n)
> errqm_ns1
[1] 4.520068
> errel_ns1=errqm_ns1/media_ns1
> errel_ns1
[1] 0.1543036
> # errore relativo 15 %
FINE RISULTATI PRIMA ROUTINE
SECONDA ROUTINE SENZA IL CALCOLO DEGLI ERRORI (si lascia il loro calcolo al lettore)
library(graphics)
nt=6 # numero molecole nel box di sinistra al tempo zero
n=30 # numero dei passaggi
nc=runif(n, min=0, max=1) # n numeri pseudo-casuali compresi fra 0 e 1
ns=c()
ns=ns[1:n]=0 # azzero gli elementi del vettore ns che registrerà il numero delle presenze nel box di sinistra
ns[1]=nt
for(i in 1:(n-1)){ n1=ns[i]-1/nt
if(nc[i]<=n1) ns[i+1]=ns[i]-1 else ns[i+1]=ns[i]+1
}
ns # 30 valori
x=c(1:30)
plot(x,ns, type=”l”)
—————————————————————————–
IL PROGRAMMA OCTAVE (MATLAB FREE) E LA FRECCIA DEL TEMPO
dott. ing. Michele Franchi, co-fondatore e direttore tecnico di PITOM snc (http://www.pitom.eu)
Attenzione! Nella nuova versione possibile selezionare quanti passaggi iniziali non considerare nei calcoli statistici. Si consiglia di non considerare i primi 100 passaggi. Si consiglia inoltre di non far visualizzare l’animazione nel caso di un elevato numero di iterazioni e/o molecole. L’animazione fa si che la simulazione rallenti moltissimo già nel caso di 200 iterazioni e 10 molecole.
Usiamo il programma Octave per ‘costruire’ il grafico della Freccia del Tempo di Boltzmann.
ISTRUZIONI
1) Installare Octave, scaricandolo gratuitamente da Internet.
2) Ricopiare gli scripts che seguono, anche con copia-incolla, per es. nel Blocco Note e memorizzarli poi col nome ‘frecciaDelTempo.m’ ed ‘animationPlot.m’ in una directory aperta nel proprio PC, per es. in C 
octaveScript.
SCRIPTS DELLA FRECCIA DEL TEMPO IN OCTAVE ‘ File “frecciaDelTempo.m”
clc clear all disp('############################# ') disp('# [START] Freccia Del Tempo # ') disp('############################# ') disp('') disp('') % INIZIALIZZAZIONE VARIABILI n = 0; % [Ingresso] Numero di iterazioni da calcolare nd = 0; % [Ingresso] Numero iniziale di molecole nel box DX nt = 0; % Numero totale di molecole n1 = 0; % Probabilità di attraversamento di una molecola da SX a DX media = 0; % Media del numero di molecole nel box SX devStd = 0; % Deviazione standard del numero di molecole nel box SX err = 0; % Coefficiente di variazione del numero di molecole nel box SX stat_start = 0; % Campione iniziale da cui calcolare le statistiche aux = 1; % Variabile ausiliaria di sistema while (aux == 1) n = input ("Quante iterazioni vuoi calcolare (N)? [200...4000]\n"); aux = 0; if (n > 4000) disp('') disp('[WARNING] Attenzione il dato inserito risulta maggiore di 4000') disp('Reinserirlo...') aux = 1; else if (n < 200) disp('') disp('[WARNING] Attenzione il dato inserito risulta minore di 200') disp('Reinserirlo...') aux = 1; else disp('OK!') end end disp('') end ns = zeros(1,n); %[Ingresso] Numero iniziale di molecole nel box SX aux = 1; while (aux == 1) stat_start = input (strcat("Quanti campioni iniziali vuoi escludere dalle statistiche? [1...",num2str(n),"]\n")); aux = 0; if (1 > stat_start) disp('') disp('[WARNING] Attenzione il dato inserito risulta minore di 1') disp('Reinserirlo...') aux = 1; else if (n < stat_start) disp('') disp(strcat("[WARNING] Attenzione il dato inserito risulta maggiore di (",num2str(n),")")) disp('Reinserirlo...') aux = 1; else disp('OK!') end end disp('') end aux = 1; while (aux == 1) ns(1) = input ("Quante molecole ci sono inizialmente nel box di sinistra?\n"); aux = 0; if (ns(1)<0) disp('') disp('[WARNING] Il numero di molecole deve essere maggiore o uguale a 0...') aux = 1; else disp('OK!') end disp('') end aux = 1; while (aux == 1) nd = input ("Quante molecole ci sono inizialmente nel box di destra?\n"); aux = 0; if (nd<0) disp('') disp('[WARNING] Il numero di molecole deve essere maggiore o uguale a 0...') aux = 1; else disp('OK!') end disp('') end aux = 1; while (aux == 1) enable_animation = input ("[Sconsigliato per un numero elevato di iterazioni e/o molecole]\nVuoi vedere l'animazione [s/n]?\n","s"); aux = 0; enable_animation = strtrim(enable_animation); if~(strncmpi(enable_animation,"s",1)||strncmpi(enable_animation,"n",1)) disp('') disp('[WARNING] Non ho capito...') aux = 1; else disp('OK!') end disp('') end % Calcolo molecole totali nt = ns(1) + nd; disp('') disp('@@@@@@@@@@@@@@@@@@@@@@@@@') disp('@ INIZIO LA SIMULAZIONE @') disp('@ ATTENDERE! @') % Per ogni iterazione... for i = 1:(n) % Calcolo probabilità attraversamento molecola SX -> DX n1 = ns(i)/nt; % Se non siamo nell'ultima iterazione... if (i < n) % ...se la probabilità calcolata è... % ...minore o uguale di un numero randomico uniformemente distribuito... % ...nell'intervallo (0,1) [Mersenne Twister algorithm with a period of 2^19937-1]... if (rand <= n1) % ...avviene il passaggio di una molecola da SX a DX ns(i+1) = ns(i)-1; % ...altrimenti... else % ...avviene il passaggio di una molecola da DX a SX ns(i+1) = ns(i)+1; end end end % Calcolo la media del numero di molecole a SX a partire dal campione "stat_start" media = mean(ns(stat_start:n)); % Calcolo la deviazione standard del numero di molecole a SX a partire dal campione "stat_start" devStd = std(ns(stat_start:n)); % Calcolo il coefficiente di variazione del numero di molecole nel box SX er = devStd/media; disp('@ SIMULAZIONE TERMINATA @') disp('@@@@@@@@@@@@@@@@@@@@@@@@@') disp('') disp("Risultati statistici relativi al numero di molecole nel box SX:") disp(strcat("Media:\n",num2str(media))); disp(strcat("Deviazione standard:\n",num2str(devStd))); disp(strcat("Coefficiente di variazione:\n",num2str(er))); % GRAFICI if(strncmpi(enable_animation,"s",1)) animationPlot(ns,n,nt) end figure plot(1:n,ns) titlePlot = strcat("SIMULAZIONE DI BOLTZMAN\nmedia = ",sprintf("%6.3f", media),";",... " devStd = ",sprintf("%6.3f", devStd),";",... " er = ",sprintf("%6.3f", er),";\n",... " ns = ",num2str(ns(1)),";",... " nd = ",num2str(nd),";",... " passaggi = ",num2str(n)); title(titlePlot) ylabel ("N. molecole box SX"); xlabel ("Iterazioni (i)"); drawnow; % SALVATAGGIO SU FILE currentDateTime = strftime ("%Y-%m-%d_%H-%M-%S", localtime (time ())); currentParameters = strcat ("_Prameters_",num2str(ns(1)),"_",num2str(nd),"_",num2str(n)); filename = strcat(currentDateTime,currentParameters,".csv"); % Salvo nella cartella di lavoro un file con i valori del vettore ns nella prima colonna % Il nome del file è del tipo "aaaa-mm-gg_hh-mm-ss_Parameters_ns(1)_nd_n.csv" dove: % aaaa-mm-gg_hh:mm:ss --> sono la data e l'ora di creazione del file % ns(1) --> è il numero iniziale di molecole nel box SX % nd --> è il numero iniziale di molecole nel box DX % n --> è il numero di iterazioni scelto dlmwrite (filename, ns', ';') disp('') disp('') disp('########################### ') disp('# [END] Freccia Del Tempo #') disp('########################### ') disp('') disp('')File “animationPlot.m”
function animationPlot (ns_array,n_step,nt) figure box_width = 10; box_height = 10; box_X_points = 0:1:box_width; box_Y_points = 0:1:box_height; plot(box_X_points,box_height*ones(box_width+1,1),'-k','LineWidth',4); hold on plot(box_X_points,0*ones(box_width+1,1),'-k','LineWidth',4); hold on plot(box_width*ones(box_width+1,1),box_Y_points,'-k','LineWidth',4); hold on plot(0*ones(box_width+1,1),box_Y_points,'-k','LineWidth',4); hold on plot((box_width/2)*ones(2,1),[box_height, (box_height/2)+1],'-k','LineWidth',4); hold on plot((box_width/2)*ones(2,1),[0, (box_height/2)-1],'-k','LineWidth',4); hanlder_mol = zeros(nt,1); handler_title = 0; for step = 1:n_step num_mol_SX = ns_array(step); num_mol_DX = nt - num_mol_SX; if(step > 1) delete(handler_title); end handler_title = title(strcat("N. SX: ",num2str(num_mol_SX)," N. STEP: ",num2str(step), " N. DX: ",num2str(num_mol_DX))); for i = 1:nt hold on if(step == 1) if(i <= num_mol_SX) hanlder_mol(i) = plot(((box_width/2)-1)*rand() + 0.5,(box_height-1)*rand() + 0.5,'or','MarkerEdgeColor','r'); else hanlder_mol(i) = plot((box_width/2) + ((box_width/2)-1)*rand() + 0.5,(box_height-1)*rand() + 0.5,'ob','MarkerEdgeColor','b'); end else if(i <= num_mol_SX) set(hanlder_mol(i),'XData',((box_width/2)-1)*rand() + 0.5,'YData',(box_height-1)*rand() + 0.5,... 'MarkerEdgeColor','r'); else set(hanlder_mol(i),'XData',(box_width/2) + ((box_width/2)-1)*rand() + 0.5,'YData',(box_height-1)*rand() + 0.5,... 'MarkerEdgeColor','b'); end end end drawnow; end endfunction3) Lanciare Octave 3.1) Impostare come directory di lavoro quella contenente lo script con il comando (es. digitare nella shell di Octave ‘cd c:\octaveScript’) 3.2) Lanciare lo script scrivendo nella shell il nome del file (‘frecciaDelTempo’) 3.3) Inserire i dati richiesti 3.4) Nella directory di lavoro impostata verrà creato un file con formato del nome “aaaa-mm-gg hh:mm:ss media_devStd_er%_ns(1)_nd_n.csv” dove: aaaa-mm-gg hh:mm:ss –> sono la data e l’ora di creazione del file ns(1) –> è il numero iniziale di molecole nel box SX nd –> è il numero iniziale di molecole nel box DX n –> è il numero di iterazioni. Questo file conterrà nella prima colonna il numero di molecole presenti nel box di sinistra ad ogni iterazione. Il file è in formato csv ed utilizza il ‘;’ come separatore. ATTENZIONE: IN OCTAVE I NOMI SONO CASE SENSITIVE, OVVERO SI FA DISTINZIONE TRA LETTERE MAIUSCOLE E MINUSCOLE. ATTENZIONE: SI RACCOMANDA DI UTILIZZARE CARTELLE CON PERCORSI SENZA SPAZI O CARATTERI PARTICOLARI. Dopo un certo tempo (quindi alla fine delle immissioni attendere!) che varia con il numero dei passaggi scelto apparirà il grafico del numero delle molecole di sinistra col tempo. Da continuare Dobbiamo aggiungere a questo post altri articoli sul concetto di tempo!
Testi rivisitati da ‘Il Sillabario’ già incontrati sul blog
Testo rivisitato da il ‘Sillabario’ n.
Il sillabario 2013 