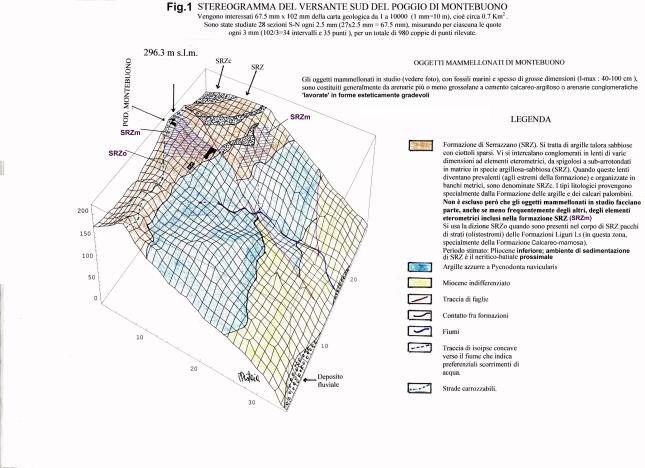
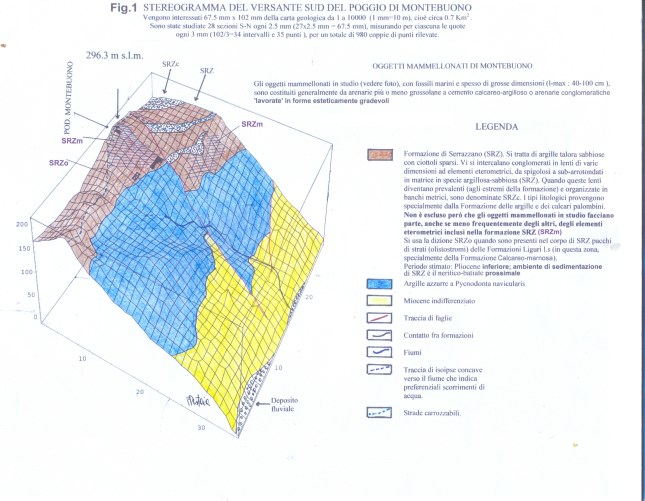
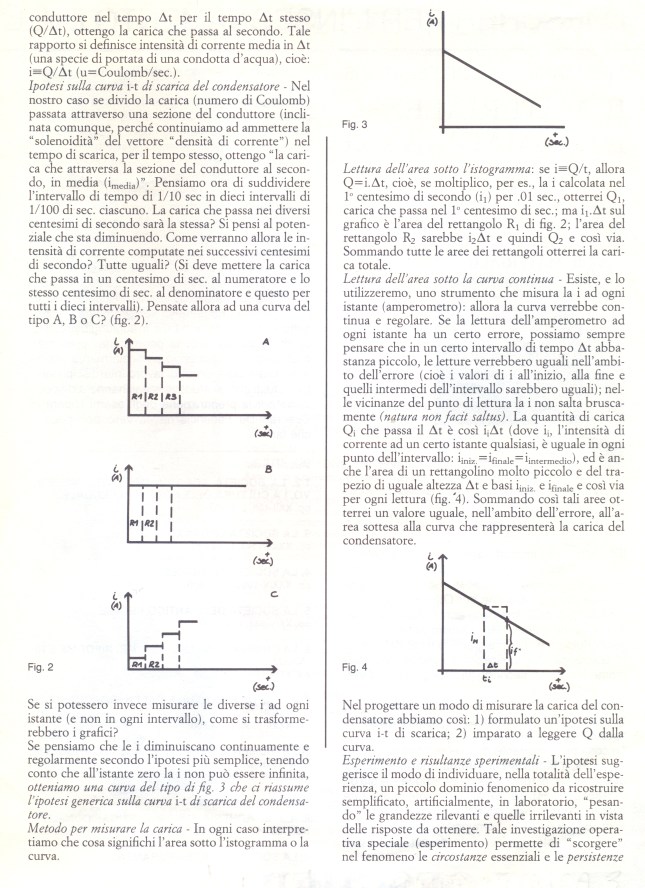
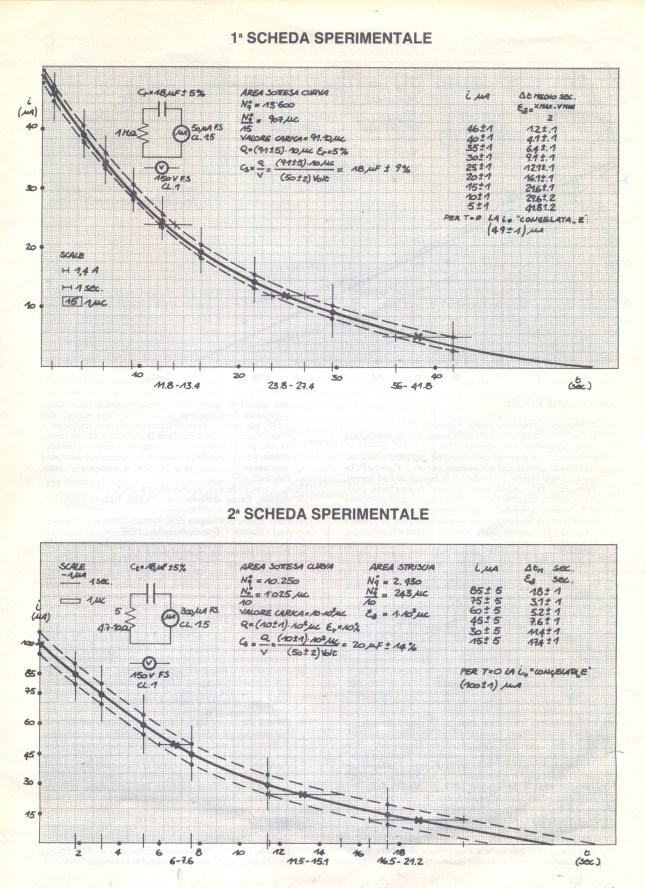
Post in via di sviluppo
CURRICULUM DI PIERO PISTOIA
PREMESSA
Nel lontano novembre 1987 fu pubblicato nella rivista Didattica delle Scienze (La Scuola, Brescia) un mio articolo, che integra quello qui di seguito riportato del febbraio 2001, della stessa casa editrice, dal titolo “LA TEORIA DELL’ERRORE E L’USO DEL COMPUTER IN LABORATORIO: un metodo di insegnamento della fisica nel biennio della Scuola Superiore”. Richiamato e rilanciato in qualche modo dallo scritto che segue, verrà riproposto alla fine di quest’ultimo, senza però la trascrizione della decina di pagine di listati relativi alla teoria dell’errore scritti dall’autore nel linguaggio Basic dell’APPLE IIe. Se ci fossero interessati, potrei trasferire anche questi scripts, anche se ormai per una macchina obsoleta. Però al tempo furono proposti dal sottoscritto e utilizzati direttamente dagli studenti con efficacia per anni nel laboratorio di Fisica. Con essi si potevano costruire anche grafici orizzontali e cartesiani con areole dell’errore per il controllo sui dati sperimentali (vedere articolo). Potrebbero essere tradotti in altri linguaggi (Mathematica di Wolfram, linguaggio R, Octave ecc.). Mandare richiesta a ao123456789vz@libero.it
In ultimo trascriviamo anche l’articolo dello stesso autore dal titolo “LETTURE DI FISICA ELEMENTARE – LA CADUTA DEI GRAVI A QUASI QUATTRO SECOLI DA GALILEO: analisi e significati di alcune sottigliezze nell’insegnamento della Fisica al Biennio Superiore” che con gli altri due completa il quadro di un metodo di insegnamento particolare per la Fisica nella Scuola. L’articolo è stato scritto ormai da tempo, ma lascio ai curiosi giudicare se non sia ancora piuttosto attuale!
Piero Pistoia
INDICE DEL POST CON LINKS
1 – UN PROGRAMMA PER CALCOLARE GLI ERRORI SU GRANDEZZE DERIVATE.
1 – PROG. PER ERRORI SU GRANDEZZE DERIVATE
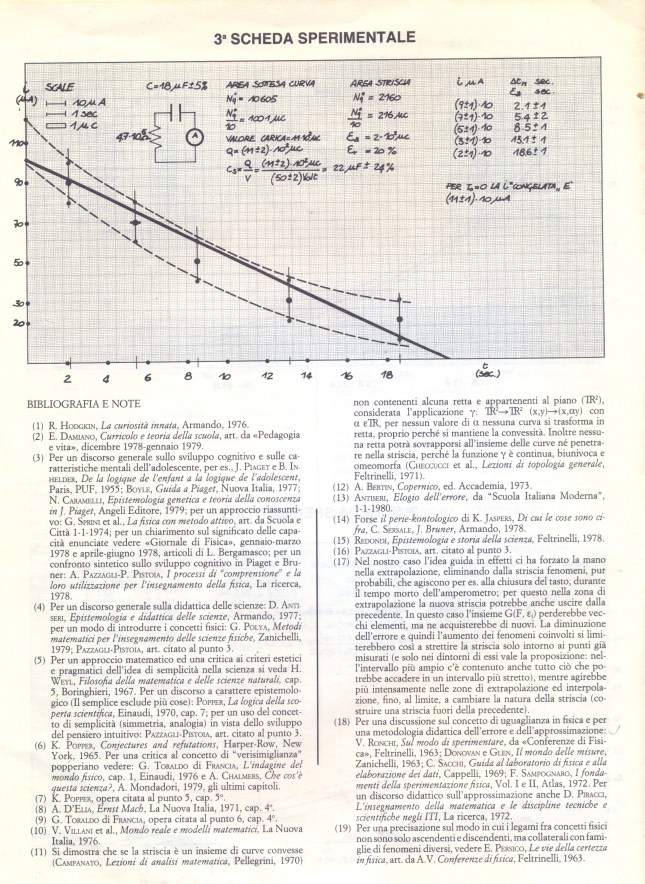
2 – LA TEORIA DELL’ERRORE E L’USO DEL COMPUTER IN LABORATORIO: un metodo di insegnamento della fisica nel biennio della Scuola Superiore.
2 – ERRORE E USO DEL COMPUTER IN LABORATORIO
3 -LETTURE DI FISICA ELEMENTARE – La caduta dei gravi a quasi quattro secoli dopo Galileo: analisi e significati di alcune sottigliezze nell’insegnamento della fisica al Biennio Superiore
3 – LETTURE DI FISICA ELEMENTARE
PER INGRANDIRE LO SCRITTO CLICCACI SOPRA!
1 – PROG. ERRORI SU GRANDEZZE DERIVATE
Per confrontare e correggere eventuali errori nel lungo e complesso listato trasferisco direttamente qui gli scripts del Qbasic, riportati nel file sotto errore1.pdf, ripresi dal file ERRORE.BAS che ‘gira’ perfettamente.
2 – ERRORE ED USO DEL COMPUTER IN LABORATORIO
INSERIAMO L’ARTICOLO SULL’ERRORE DEL 1987 di Piero Pistoia
3 – LETTURE DI FISICA ELEMENTARE
POSSONO SEGUIRE I PROGRAMMI IN BASIC APPLE IIe RELATIVI ALL’ARTICOLO PRECEDENTE
———————————————————
Attenzione! l’articolo che segue è in via di costruzione; verrà corretto man mano che procede.
LETTURE DI FISICA ELEMENTARE
LA CADUTA DEI GRAVI A QUASI QUATTRO SECOLI DA GALILEO
Analisi e significati di alcune sottigliezze nell’insegnamento della Fisica al Biennio Superiore
di PIERO PISTOIA
INTRODUZIONE
Riteniamo giustificato, secondo criteri epistemologici (1), psicologici (2) e didattici (3), un metodo di insegnamento della Fisica non di tipo induttivista, ma caratterizzato da particolari processi ipotetico-deduttivi. Consideriamo altresì che il così detto metodo sperimentale di Galileo, alla luce anche delle recenti interpretazioni del suo pensiero (4), abbia in effetti analoghe caratteristiche.
Secondo tale metodo l’insegnamento deve partire da problemi (nell’accezione data a questa parola da Popper, Antiseri et. al.), per arrivare, attraverso le “Teorie tentative” di soluzione (TT di Popper), all’ “Eliminazione Critica dell’errore” (EE i Popper), fase riassunta dalla “Discussione e Argomentazione Critica” e/o dal processo sperimentale di controllo, fino alla formulazione del nuovo problema.
Diversi sono i problemi che devono essere affrontati in successione per costruire in classe la disciplina, sotto la guida dell’insegnante, alcuni dei quali, importanti ed obbligati, in quanto innescano a cascata una sequenza di altri, sono, a mosaico, qui di seguito nominati.
a – Nella caduta dei gravi (per es., con attrito trascurabile e velocità iniziale zero m/sec), che relazione ci sarà fra velocità istantanea e tempo o fra velocità istantanea e spazio percorso?
b – Che relazione ci sarà fra modulo della forza applicata ad un oggetto che può muoversi liberamente, con attrito trascurabile, su un piano orizzontale, e il modulo della sua accelerazione acquistata?
c – Che relazione ci sarà fra quantità di carica elettrica posta su un conduttore isolato o su un’armatura di un condensatore e il potenziale elettrico da esso assunto o la differenza di potenziale fra le due armature? (5)
d – Che relazione ci sarà fra la differenza di potenziale (Va-Vb) misurata ai capi di un resistore e l’intensità di corrente (Ic) in una sezione di esso?
e – Che relazione ci sarà fra il flusso di Induzione magnetica concatenata ad un circuito percorso da corrente e l’intensità di corrente in esso circolante?
Ognuno di questi problemi e dei molti altri non nominati deve essere discusso in classe fino a formulare una o più ipotesi plausibili relativamente alla discussione iniziale attivata, non necessariamente “vere”, per poi guidare una discussione logico-critica innescata sul background culturale della classe ( es.,si vedano i teoremi galileiani in ‘Esperimenti Pensati’) o per progettare in laboratorio un esperimento di controllo, dopo magari una trasformazione analitica della relazione iniziale in una proposizione più agile da sperimentare (es., v/t=k in s/t^2=k/2). Nella zona di corroborazione o di falsificazione dell’ipotesi nascerà il nuovo problema.
In questo lavoro l’autore cercherà di analizzare il problema siglato a, precisandone aspetti ed implicazioni educative e formative, riscoprendo nella caratteristica dialogica galileiana di condurre il discorso e nei precisi e puntuali interventi di Salviati nei confronti di Semplicio, la chiave per ricostruire la Fisica anche nelle classi di oggi.
ANALISI E DISCUSSIONE DEL PROBLEMA RELATIVO ALLA CADUTA DEI GRAVI (PROBLEMA a) E FORMULAZIONE DELLE IPOTESI
Focalizziamo l’attenzione e la memoria degli alunni sulla caduta i oggetti pesanti (gravi) sui quali le azioni di disturbo dell’aria sono meno evidenti, almeno per basse velocità. Alla domanda che cosa faccia la velocità durante il movimento, si hanno in generale perplessità nella classe. I nostri ragazzi di 14-15 anni hanno e devono avere la mente del Semplicio galileiano. Alcuni però conoscono già le risposte a memoria, fornite probabilmente come nozioni isolate nei corsi precedenti, prima che fossero sorti sull’argomento interrogativi, prima che fossero formulate le ipotesi, prima che si precisassero le aspettative, prima delle delusioni dinanzi ad ipotesi sbagliate, prima insomma dei processi che catalizzano il vero apprendimento. Qualche frammento di ricordo culturale precedente scarsamente assimilato, certi mass media, certi personal media, qualche software selvaggio e poco calibrato, avranno fornito queste nozioni fini a se stesse.
Il maggior tradimento che la civiltà tecnologica abbia mai perpetrato ai danni dei cuccioli della specie, è proprio questo: sono stati gettati in un contesto tecnologico di natura altamente simbolica e lontano così dalle teorie del senso comune e del buon senso a cui gli alunni sono vicini, in un mondo incomprensibile, nel quale i messaggi si trasformano in nozioni isolate da memorizzare e delle quali sfuggono le ragioni più profonde, in un mondo dove i “messaggi” svuotati da “mezzo”, per mutuare le parole da McLuan, annebbiano curiosità e meraviglia, molle del progresso umano.
Fortuna che c’è ancora qualche Semplicio che vede cadere il grave subito velocemente, appena lasciato. Allora a guisa di Salviati galileiano , l’insegnante deve guidare la discussione, al di là di tutto: del tempo del programma, delle scadenze e dei voti; il cucciolo dell’uomo ha il diritto di imparare a costruirsi i propri modelli razionali per interpretare il mondo, graduali ed efficaci. E’ solo in questa prospettiva che ha significato l’aggettivo ‘formativo’ che attribuiamo all’insegnamento della Fisica al Biennio Superiore.
Il sasso aumenta di velocità perchè urta la mano, che cerca di fermarlo, con più violenza a maggior spazio percorso e al passare del tempo. Tale sforzo della mano è legato all’impulso su essa legato alla prima potenza della velocità, o, se ci riferiamo all’energia necessaria, essa è legata alla seconda potenza della velocità: questo noi lo sappiamo, ma l’alunno Semplicio non lo può sapere!
In ambedue i casi, usando così il criterio di semplicità, la prima ipotesi che viene in mente agli alunni è la diretta proporzionalità fra v e s, proprio come ebbe a pensare Galileo (6). Quando dalla discussione di un problema concludiamo che all’aumentare di una grandezza anche l’altra, alla prima correlata, aumenta (o dimunuisce), ‘spariamo’ l’ipotesi più semplice di diretta (o inversa) proporzionalità, a meno che ulteriori approfondimenti della discussione non suggeriscano altrimenti ( caso per es., della relazione fra forza gravitazionale e distanza, da affrontare in altro lavoro ()). Scrivere oggi v=k * s sembra non abbia senso (vedere dopo), per ragioni però troppo lontane dall’intuito del nostro alunno Semplicio, se lo stesso Salviati in prima istanza cadde anch’egli nella trappola. Quindi è da ritenere importante che di tale relazione, rimanga traccia nella mente dell’alunno nonostante tutto, anche se poi verrà abbandonata.
Così la classe formulerà due ‘teorie tentative’ possibili per la soluzione del problema della caduta dei gravi, con le nostre condizioni al contorno:
1 – La v-istantanea e s direttamente proporzionali.
2 – La v-istantanea e t direttamente proporzionali.
PRECISAZIONI E SOTTIGLIEZZE CHE SORGONO DALL’ANALISI DELLE DUE IPOTESI
Non è così immediato intuire per gli alunni che le due ipotesi non sono la stessa cosa. Dobbiamo così rifarci alla matematica elementare del moto uniformemente accelerato (già spiegato fra i modelli razionali per “leggere” un moto); se v e t sono direttamente proporzionali, si dimostra con la matematica elementare e graficamente che v ^2 e s sono direttamente proporzionali e non v e s. Così nel dire ve t e nel dire v e s direttamente proporzionali, si vengono ad enunciare due ipotesi diverse ed alternative.
Anche lo stesso Galileo davanti allo stesso problema formulò proprio le stesse due ipotesi, anche se su v=k*s ebbe quasi subito dei dubbi. Infatti dopo aver enunciato tale ipotesi in una lettera a Paolo Sarpi, nei “Discorsi e dimostrazioni matematiche”, faceva dire per bocca di Salviati:
“Quando le velocità hanno la medesima proporzione che gli spazzi passati o da passarsi, tali spazi vengono passati in tempi uguali: se dunque le velocità con le quali il cadente passa lo spazio di 4 braccia furon doppie delle velocità con le quali passò le due prime braccia – appartenenti alle 4 precedenti (nota dell’autore) – (sì come lo spazio è doppio dello spazio), adunque i tempi dei passaggi sono uguali”
Questa fu la sua argomentazione critica (EE di Popper). Nello stesso moto si verrebbero a percorrere nello stesso tempo un dato intervallo di spazio e la sua metà appartenente ad esso, cosa che può accadere solo se il movimento è istantaneo (velocità infinita). Se v=k*s, chiaramente la velocità istantanea alla fine delle prime 4 braccia è doppia della velocità alla fine delle due braccia. Ma continuando ad argomentare, affermare questo però non vuol significare che anche la velocità media debba essere doppia e quindi il tempo uguale, di qui l’assurdo. Se si considera doppia la velocità media delle 4 braccia rispetto alle due, si introduce tacitamente anche la seconda ipotesi v=k * t; infatti solo in tal caso vm=(vf+0)/2!
In effetti Galileo nell’affermare che la velocità nel passare 4 braccia era doppia della velocità nel passare 2 braccia, secondo l’autore, tacitamente veniva ad inserire nel ragionamento anche l’ipotesi v=k * t (che permetteva una velocità media doppia). Sempre secondo l’autore il ragionamento galileiano in effetti viene a significare che, se valgono contemporaneamente v= k * s e v=k * t, si arriva ad un assurdo. Se questa immediata interpretazione non convince, si vedano le altre più qualificate e profonde sorte ultimamente in ambiente accademico (7) (8).
Il fatto che la discussione galileiana su un problema presenti varie sfaccettature, il fatto che esistano più modi di argomentare sull’ipotesi conseguente, non significa che non si debba, come faceva Galileo – non necessariamente allo stesso modo – discutere su problemi per tentare soluzioni prima o al posto dell’esperimento. Chi vede in questo pericoli di ambiguo verbalismo, non coglie significati profondi di un corretto discorso epistemologico e psicologico sui processi di acquisizione della conoscenza e, quello che è più grave, potrebbe sviare gli interventi per un recupero delle situazioni tutt’altro che rosee focalizzate dai diversi tests piagettiani sull’intelligenza formale del giovane (9) (10).
Consapevolmente o no, Galileo, secondo l’autore, dimostra la non coincidenza delle due ipotesi e così verrà fatto nell’insegnamento: si formuleranno le due ipotesi e si dimostrerà in qualche modo che sono diverse e alternative; se è corroborata l’una l’altra verrà scartata.
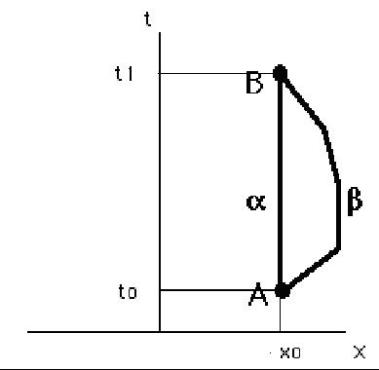
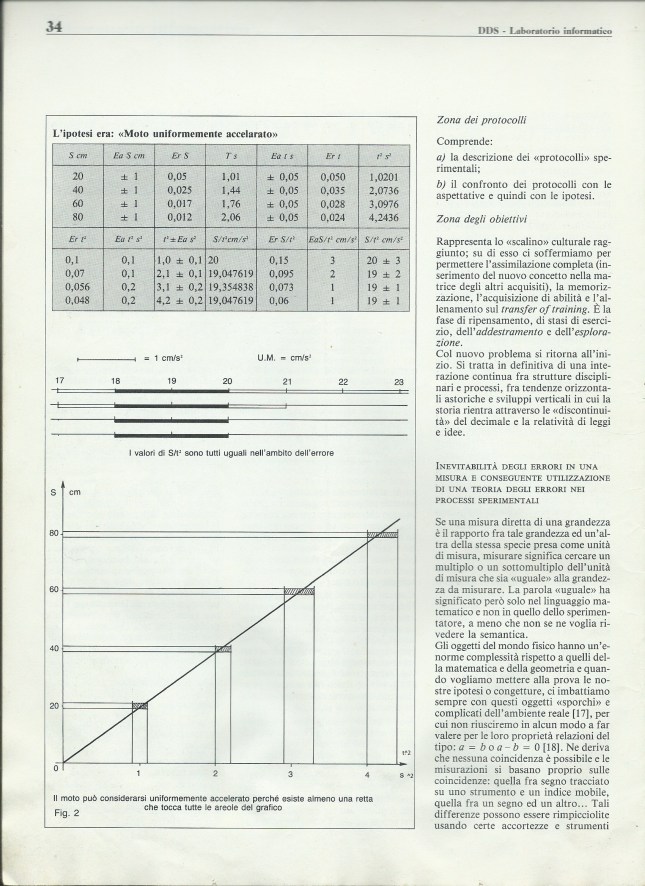
Si passerà poi a controllare in laboratorio l’ipotesi v/t=k, che fornisce come proposizione sperimentabile s/t^2=k/2. Con l’asserzione_base s/t^2=k/2, che è appunto la formulazione sperimentabile di v/t=k, andiamo in laboratorio per il controllo. In realtà l’ipotesi in un certo “RANGE” di errore viene corroborata.
Siamo così arrivati a concludere che l’oggetto (per es., una sferetta di acciaio, se si utilizza un’apparecchiatura Leybold) cade di moto uniformemente accelerato e quindi la relazione fra velocità e spazio è del tipo v^2/s=2*k, moto materialmente possibile, mentre la relazione v=k*s rimane esclusa sperimentalmente in quanto alternativa e irriducibile all’altra. L”ipotesi sperimentabile v^2/s=2*k non era però così intuibile come l’altra, per cui non veniva formulata in prima istanza. Chiaramente le due ipotesi v= k*t e v^2=2ks sono la stessa cosa analiticamente.
Rimangono ora da precisare alcune sottigliezze implicate nel significato di k e quindi formulare il nuovo problema da affrontare nella successiva unità didattica. Prima però analizziamo brevemente il significato matematico e fisico delle ipotesi v/s=k e v^2 /s=2k.
ALCUNE CONSIDERAZIONI FISICO_MATEMATICHE SU v/s=k e v^2 /s=2k
Analisi fisico matematica dell’ipotesi v=ks
L’ipotesi è espressa dall’eq. differenziale a variabili separabili dx/dt = k*(x-xo). Dall’analisi di essa, non so se possibile ai tempi di Galileo, deriva che, per la ricerca delle soluzioni, è necessario porre la condizione x-xo <>0 pe cui nel processo si perderebbe la soluzione x-xo= 0 metri, per cui x=xo è un punto di discontinuità per la funzione integranda che risulta continua per x<xo e x>xo.
Significato della soluzione x-xo =0
Al tempo t=0 sec, quando x=xo, la velocità è zero e, non potendo aumentare x, non aumenta v, per cui x=xo viene ad essere costante al passare del tempo: l’oggetto non potrà muoversi. Invece l’eq. dx/dt = k*t fornisce per t = 0 sec ancora v=0 m/sec, però il tempo “passa”, per cui la v può aumentare fornendo le altre soluzioni.
x = xo sarebbe l’unica soluzione, ma si perde nel processo di calcolo?!
Analisi matematica e fisica dell’ipotesi v^2 /s=2k
L’analisi dell’ipotesi v^2 /s =2*k, fornisce un modello fisico funzionale:
(dx/dt)^2 =2k*(x-xo)
dx/dt =+/-SQR(2k)*SQR(x-x0) e separando le variabili e integrando fra xo e x:
2*SQR(x-xo)-0 =+/-SQR(2k)*t ed elevando a quadrato:
4*(x-xo) =2k*t^2
Ma, al di là di tutto, ciò che insegna Galileo è il modo scientifico di condurre il processo, il modo di discutere il problema, sezionandolo con tutti gli strumenti razionali conosciuti per chiarirlo e ‘sparare’ un tentativo di soluzione da sottoporre poi al vaglio dell’argomentazione critica e talora dell’esperimento. Ciò che insegna Galileo in definitiva è un modo corretto di fare lezione.
FASI SINTETICHE DEI PROCESSI RAZIONALI, DENSI DI ‘TRANSFER’, NELL’ANALISI DEL SIGNIFICATO DELLE COSTANTI DI PROPORZIONALITA’
In generale le fasi del processo razionale davanti ad un’ipotesi di diretta proporzionalità, corroborata nell’ambito dell’errore, possono essere così brevemente delineate.
1 – la grandezza derivata k non dipenderà dalle grandezze che lega, ma da altre, relative a ‘qualcosa’ di rilevante che durante l’esperimento non è cambiato. Se f/a = k, il valore di k non dipenderà dalla grandezza accelerazione, nè dalla grandezza forza (almeno nel range dell’errore sperimentale) e quindi potrebbe dipendere da qualche grandezza relativa all’oggetto con cui abbiamo sperimentato. Da quali? Se (va-vb)/Ic = k, il valore di k non dipenderà alle grandezze elettriche Differenza di Potenziale e Intensità della corrente: è facile riferirci allora a qualche proprietà del conduttore su cui abbiamo sperimentato. A quali? Se Q/V = k, il valore di k non dipenderà dalle grandezze elettrostatiche Carica e Potenziale elettrici, ma da qualche proprietà del conduttore dell’esperimento. Da quali?
2 – Il significato fisico di k nasce poi dal metterci, mentalmente, nelle condizioni di ripetere l’esperimento ottenendo un valore di k diverso. Se il k di f/a dipende dall’oggetto su cui abbiamo sperimentato, immaginando un oggetto diverso, se k verrà maggiore, a parità di forza, a sarà minore; cioè k dipenderà da una prprietà dell’oggetto che si configura come ostacolo all’accelerazione. Potrebbe essere già stata introdotta una grandezza fondamentale che misuri tale proprietà con la bilancia inerziale: la massa inerziale. Se il k di (va-vb)/Ic dipende da certe proprietà del conduttore su cui si è sperimentato, cambiandolo potremo ottenere un k diverso. Se è maggiore significherà che a parità di differenza di potenziale, avrò una Ic minore: k si configura come una specie di ostacolo al passaggio della corrente (resistenza elettrica). Una successiva argomentazione può precisare la dipendenza di R dalle grandezze geometriche del filo…. Si innescano una successione di problemi a cascata da affrontare in successive unità didattiche. Se il k di Q/V dipende dal conduttore, cambiandolo dovrebbe cambiare k: se k è maggiore significhera che posso mettere su tale conduttore più Carica, a parità di potenziale; cioè k ha il significato di Capacità elettrica. Una successiva discussione potrà precisare la dipendenza di C dalle altre grandezze e così via.
3 – Precisazione concettuale delle grandezze investigate. Come si vede si tratta d i veri e propri processi razionali che si ripetono in ambienti diversi (transfer di Bruner), favorendo il transfer concettuale all’interno della disciplina ( Transfer specifico), attraverso il potente Principio di Continuità galileiano (E. Mach). Galileo adattava gradualmente le sue elucubrazioni mentali ai fatti, tenendo fermi questi pensieri fino alle estreme conseguenze. Il Principio di Continuità consiste nel variare nella mente gradualmente le circostanze di un caso particolare, tenendo fermo nello stesso tempo l’idea già formulata su di esso (metodo che facilità la comprensione di tutti i fenomeni naturali con un fatica intelletuale minore rispetto ad altri processi.
ASPETTI RELATIVI AI SIGNIFICATI DELLA COSTANTE DI PROPORZIONALITA’ FRA v e t
Abbiamo corroborato in laboratorio l’ipotesi v/t=k nella sua forma meglio sperimentabile (s/t^2=k/2); k ha le dimensioni di una accelerazione e, proprio perchè non cambia, non dipenderà dalla v, che cambia, nè dal tempo. Potrei così , sulla falsa riga degli esempi accennati al paragrafo precedente, affermare che k venga a dipendere da qualche proprietà dell’oggetto che ho usato per l’esperimento. Tale congettura è abbastanza plausibile a questo stadio: un oggetto più ‘pesante’, per es., può avere accelerazione di caduta diversa…. Cioè, dire che k dipende da qualche proprietà dell’oggetto può voler significare, per es., che oggetti più pesanti potrebbero avere un k maggiore (è la congettura più frequente nelle classi, a causa dei riferimenti all’esperienza quotidiana ricordati).
Nasce così il nuovo problema sul significato di k e eventuali ulteriori problemi sulla sua dipendenza da qualche altra grandezza. formuliamo, per es., l’ipotesi che sperimentando con un oggetto più ‘pesante’, il k diventi maggiore: oggetti più pesanti cadono con maggiore accelerazione. Lasciamo, in questa fase, la discussione a questo livello basso, per sfruttare la delusione onde focalizzare l’interesse e destare ‘meraviglia’. Volendo potevamo approfondire la discussione usando anche il Teorema di Galileo sull’argomento (vedi nota n, 11), eliminando praticamente il rischio sull’ipotesi.
La classe segue motivata il nuovo esperimento e la delusione delle aspettative lascia piuttosto perplessi: la proprietà o le proprietà dalla quali dipende il nostro k non sono relative all’oggetto scelto per l’esperimento! Seguiranno argomentazioni sui presupposti che hanno portato alla formulazione dell’ipotesi sbagliata. A questo punto possiamo anche inserire il teorema galileiano, per tranquillizzare nell’immediato la classe. Si continuerà precisare anche i concetti coinvolti sperimentando col tubo di Newton.
La discussione dovrà poi procedere facendo riferimento a dati riportati su libri o riviste: tutti i corpi in assenza di attrito cadono sempre con la stessa ccelerazione nello stesso posto. Così appare importante il ‘postò’, la ‘zona di spazio’ dove avviene l’esperimento, quasi che le zone di spazio mutino le loro proprietà, muovendoci per l’universo.
Gli oggetti infatti ‘deformano’ lo spazio per mezzo i una grandezza vettoriale chiamata ‘Campo Gravitazionale’. Il nostro k è proprio tale Campo: quindi l’oggetto, le cui proprietà non cambiano durante l’esperimento, è il corpo planetarionelle vicinanze: nel nostro caso la Terra.
Il problema diventa complesso: potrà o non potrà essere sviscerato in tutte le sue parti a seconda dei livelli di comprensione e di impegno delle classi. Una cosa è certa: a quasi quattro secoli da Galileo, dobbiamo essere contenti se si trovano ancora nelle nostre scuole, nonostante mass media, personal media…, ancora i Semplicio, intelligenti anche se dotati solo di teorie del senso comune, che fanno ancora le stesse domande ingenue davanti agli stessi problemi di quattro secoli fa e quasi allo stesso modo.
Rimane da chiederci se la nostra pesante cultura del periodo post-industriale e oltre, con i suoi prodotti tecnologici così sofisticati fuori della Scuola ed anche dentro la Scuola (rotaie a cuscino d’aria, cronografi a 1/1000 di sec…) non possa creare, nella mente impressionabile dei ragazzi, sovrastrutture così artificiose da impedire i livelli di maturazione normale e il formarsi graduale di modelli calibrati di interpretazione del mondo (gradualmente sempre più simbolici) e quindi lo sviluppo armonico dell’intelligenza (9) (10)-
PIERO PISTOIA
BIBLIOGRAFIA E NOTE
1 – K. Popper “La logica della scoperta scientifica”, Einaudi, 1970; K. Popper “Congetture e confutazioni” Vol. I° e II°, Mulino,1972; K. popper 2 Conoscenza oggettiva2, Armando,1975; P. Feyerabend, T. Khun, I, Lakatos et al. “critica e crescita della conoscenza”, Feltrinelli, 1976; D. Antiseri “Epistemologia e didattica delle scienze”, Armano, 1p77; P. Redondi “Epistemologia e storia della S, Feltrinelli, 1978cienza
2 – J. Piaget e B. Inhelder “De la logique de l’enfant e la logique de l’adolescent”, Puf Paris, 1955;J. S. Bruner “Il significato dell’Educazione”, Armando, 1973; R. Mazzetti “Dewey e Bruner”, Armando, 1976.
3 – J. S. Bruner “Verso una teoria dell’istruzione”, Armando,1967: M. Laeng “L’Educazione nella Civiltà tecnologica”, Armando,1969; P. Pistoia et al. “I fondamenti psicologici ed epistemologici dell’insegnamento della Fisica” La Ricerca, Loescher, 15-12-1977; P. Pistoia et al. ” I processi i Comprensione e la loro utilizzazione per l’insegnamento della Fisica”, La Ricerca, Loescher, 15-11- 1978; P. Pistoia et al. “Alcuni presupposti psicopedagogicie ed epistemologici della Riforma della Scuola Superiore, La Ricerca, Loescher,15-3-1980.
4 – P. Wiener e A, Noland “Le radici del pensiero scientifico”, Feltrinelli, 1977; per non parlare dell’analisi del pensiero galileiano condotta da P, K. Feyerabend in “Problemi dell’Empirismo”, Milano, 1971 e in “Contro il metodo”, Milano, 1973.
5 – Per la didattica del concetto di Capacità elettrica: P. Pistoia “Considerazioni critiche su un progetto programmatico relativo al processo di Comprensione di un concetto fisico”, La Ricerca, Loescher, 15-10-1981.
6 – G. Galilei “Discorsi e Dimostrazioni matematiche”, Salani, 1964.
7 – S. Bergia-P. Fantazzini “La Fisica nella Scuola”, XIII, N. 1, 1980
8 – Elio Fabri “La Fisica nella Scuola”XIV, N. 3,1981.
9 – L: Bergamasco “Didattica e sviluppo intellettuale degli studenti”, Giornale di Fisica, Gennaio-marzo, 197
10 – P. Violino e B. Di Giacomo “Sul livello cognitivo degli alunni delle Scuole Secondarie Superiori” , La Fisica nella Scuola, Luglio-Settembre, 1981.
11 – Esperimento mentale di Galileo per dimostrare, rileggendo oggi, che, partendo da fermo, la velocità di caduta da una stessa altezza, in assenza di attrito, è la stessa per tutti i corpi di qualsiasi natura, peso e forma. Galileo in effetti al tempo della dimostrazione parla di velocità s.l. di due ‘pietre’ di diversa ‘grandezza’, che cadono senza precisare se si tratta di velocità istantanee alla stessa altezza, o velocità con cui urtano la base o se partono addirittura dalla stessa altezza (visto che il movimento aristotelico degli oggetti verso il loro Stato Naturale era uniforme e le velocità degli oggetti proporzionali al loro peso ). Comunque la dimostrazione con le precisazioni dette continua a valere per tutte le velocità istantanee ad ogni altezza nella caduta, per le velocità finali e per le velocità medie e per tutti i corpi di ogni peso natura e forma.
“Ma se questo è, ed è insieme vero che una pietra grande si muove, per esempio, con 8 gradi di velocità, ed una minore con quattro, adunque congiungendole ambedue insieme, il composto di loro si muoverà con velocità minore di otto gradi; ma le due pietre, congiunte insieme, fanno una pietra maggiore che quella prima, che si muoveva con 8 gradi di velocità; adunque questa maggiore si muove meno velocemente che la minore; che è contro vostra supposizione”.
Riteniamo












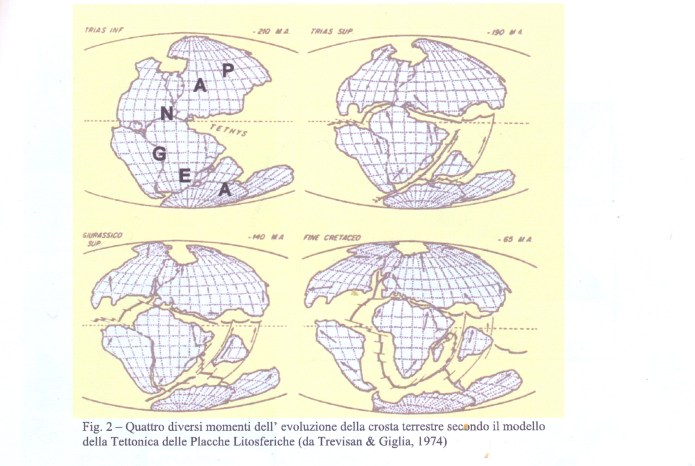
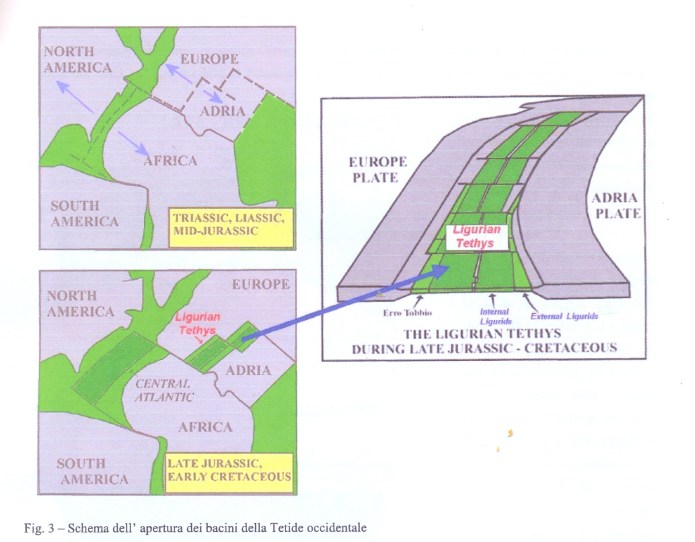
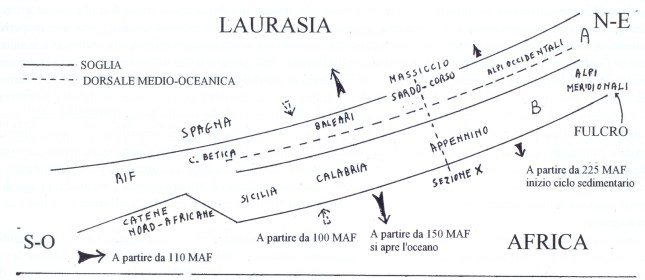
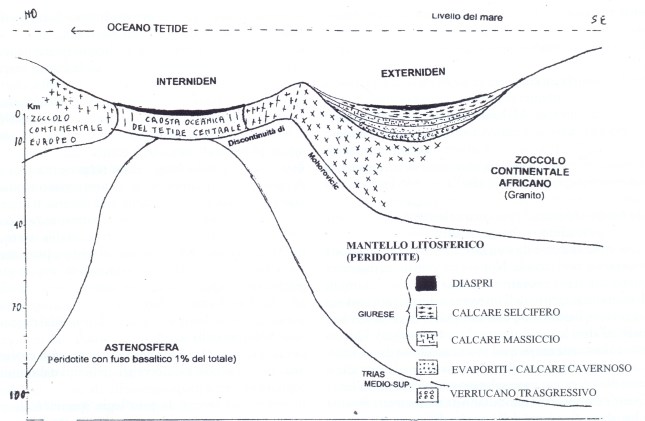
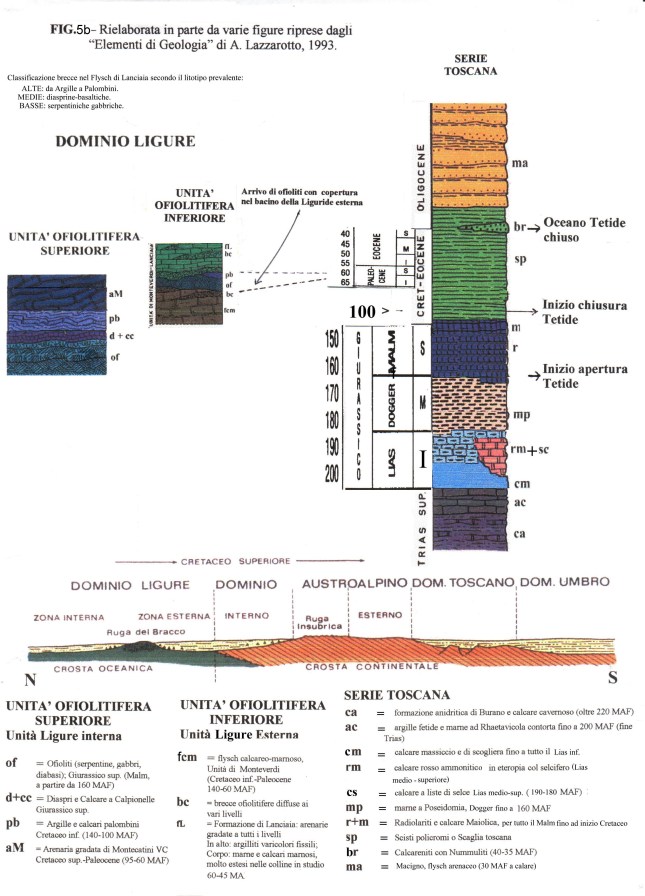
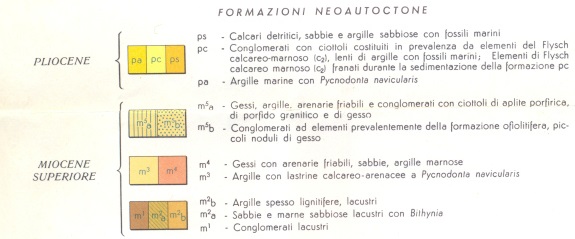
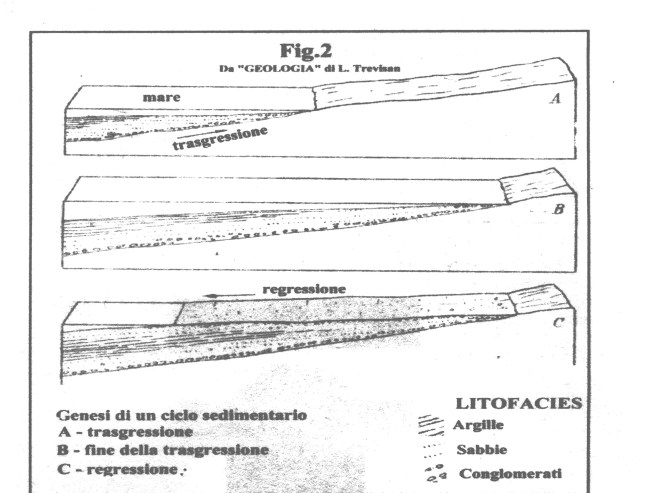
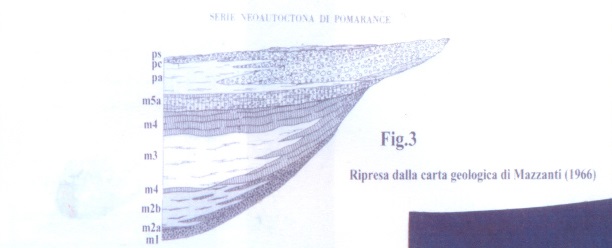
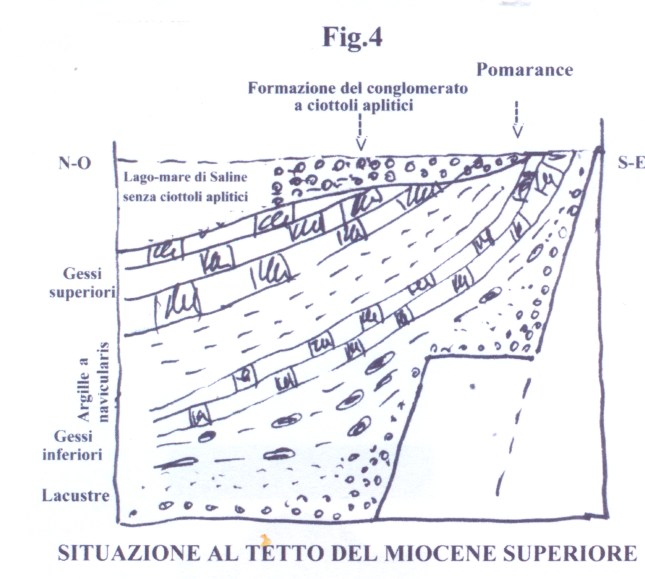
 a contatto con correnti ricche di silice colloidale e anidride carbonica. In queste condizioni si scioglieva la parte calcarea interessata da dette correnti e rimanevano gli eventuali resti silicei, mentre la presenza in soluzione di una concentrazione maggiore di Ca^++ determinava la precipitazione dei fiocchi di silice colloidale. Al cessare di queste correnti, continuava il deposito di fanghi calcarei che venivano così a inglobare noduli e straterelli di silice pura, come poi apparirà nella roccia definitiva. Tali Calcari a liste di selce continuarono a deporsi fino al Giurese superiore (circa 150 maf)
a contatto con correnti ricche di silice colloidale e anidride carbonica. In queste condizioni si scioglieva la parte calcarea interessata da dette correnti e rimanevano gli eventuali resti silicei, mentre la presenza in soluzione di una concentrazione maggiore di Ca^++ determinava la precipitazione dei fiocchi di silice colloidale. Al cessare di queste correnti, continuava il deposito di fanghi calcarei che venivano così a inglobare noduli e straterelli di silice pura, come poi apparirà nella roccia definitiva. Tali Calcari a liste di selce continuarono a deporsi fino al Giurese superiore (circa 150 maf)