APPUNTI PER UNA LEZIONE – DIBATTITO sulla “Mancanza di Motivazione” a Scuola; a cura del docente Andrea Pazzagli

Immagine | Posted on febbraio 4, 2019 by pierfrancesco1952

LA MOTIVAZIONE SCOLASTICA A CURA DI A. PAZZZAGLI

Trasferito dall’inserto ‘Il sillabario’ cartaceo

L’ASSEDIO, poesia di Pedro 12.99

Immagine | Posted on gennaio 24, 2019 by pierfrancesco1952

NB – Ad Antonio di Simone è piaciuto questo post, come da mail inviata all’Amministratore il 25-gennaio-2019.

POESIA DI PEDRO: L’ASSEDIO 12.99

RAGIONE, SENSO DELL’ARTE E DEL SACRO, idee appena abbozzate; del dott. Piero Pistoia; intermezzo: poesia di P. Fidanzi

Immagine | Posted on Maggio 5, 2017 by pierfrancesco1952

LA POESIA ARCANA DEL POETA VOLTERRANO MARCELLO VANZI con intermezzo; a cura di Piero Pistoia

Immagine | Posted on Maggio 4, 2017 by pierfrancesco1952

INTERMEZZO: pittura di Gabriella Scarciglia

MEMORIA DI PAESE

Ho riudito l’uccello piumato dei monti
librarsi davanti alle cattedrali di castagni
in questo silenzio universale di ricordo –
passaggio di un tempo felice di equinozi
quando tu – mia cara – accompagnavi
la mia trepida attesa sulle sponde
di questo paese appenninico –
e le acque dei torrenti scendevano
caste da altitudini polverose
e non c’era pensiero di morte
nei nostri occhi innamorati.
Ho riudito il passo della volpe
avvicinarsi nel brivido degli abeti –
anche allora parlavamo del rifugio
nelle sere di montagna – quando
i greggi transitavano da nord
e baciava il cielo le case del paese
con quelle ombre lunghe dietro Villa Ada
e silente il pensiero cadeva in spazi d’erbe.
Ora si torna nel perimetro sentimentale
più curvi – senza il fascino più di quelle attese –
ora i boschi ed i monti hanno il colore
crudele ed esangue delle cose perdute –
ora il paese conduce le sue gemme in questa estate –
non più pastori a chiamare crepuscoli
non più le onde degli antichi abbracci –
andiamo cara – nel vortice esasperato
di giorni ed albe lunari – nostro dolce paese – addio

(Marcello Vanzi)

Per leggere le tre poesie precedenti, con possibilità di ingrandimento, cliccare su:

(Marcello Vanzi)

Per leggere la poesia di Vanzi dal titolo “Frammenti” in pdf, trasferita dalla “Spalletta” del 19-06-2018 (direttore PIETRO GASPARRI) cliccare su:

VANZI0001

LA CREATIVITA’ COME DIFFICILE SQUILIBRIO FRA RAGIONE E IRRAZIONALITA’ della dott.ssa Franca Soldateschi

Immagine | Posted on ottobre 27, 2016 by pierfrancesco1952

Questo intervento è stato ripreso in questo blog, dal post ” MENTE E CERVELLO” (contenente ben otto articoli), per renderlo più visibile.

Per approfondire i diversi aspetti qui prospettati leggere appunto anche il post a più voci “Mente e Cervello” in questo blog.

UN PARZIALE PERCORSO DI BASE (1) SULL’ANALISI DI UNA SERIE STORICA REALE, POCO INTUITIVA, COMMENTATO CON IL LINGUAGGIO R E COL MATHEMATICA DI WOLFRAM; SUBROUTINE PERIODOGRAMMA CON ESERCIZI; del dott. Piero Pistoia

Immagine | Posted on ottobre 15, 2014 by pierfrancesco1952

POST-ZIBALDONE ARRUFFATO MA DENSO DI INFORMAZIONI (sulla analisi di dati sperimentali)

Vedere i tags (la via si fa con l’andare)

CURRICULUM DI PIERO PISTOIA

al termine del post

::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

piero-pistoia-curriculumok-1-34 Download

Problemi di inquadramento del testo

PRIMA BOZZA DI INDICE A LINKS INTERNI in via di costruzione

Links

1 – PREMESSA sullo stato dell’articolo
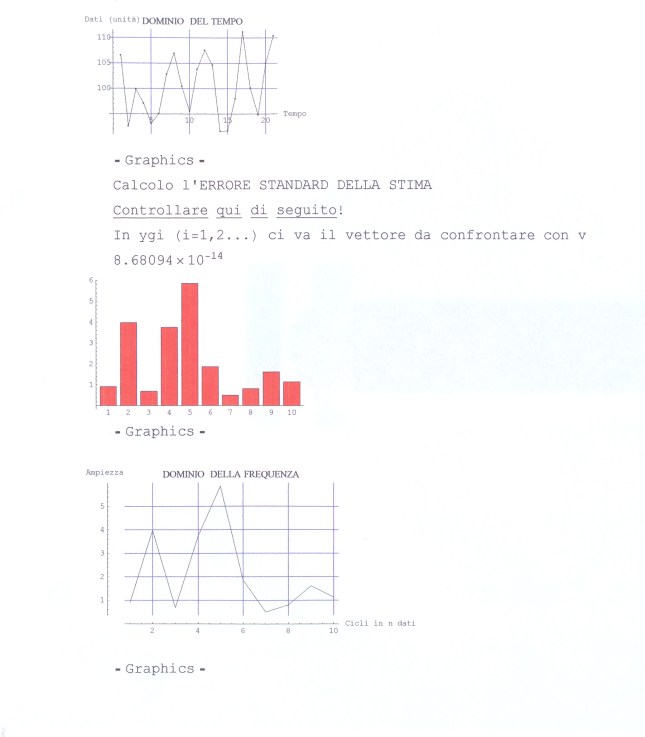
2 – IN ANTEPRIMA : la funzione PRDGRAM (scritto dal dott. Piero Pistoia) e l’esercitazione (8 esercizi) sul PERIODOGRAMMA

RIASSUNTO

PARTE I^a

Cenni operativi sui concetti di statistica implicati nell’analisi di una serie storica
Correlogramma ed il Periodogramma
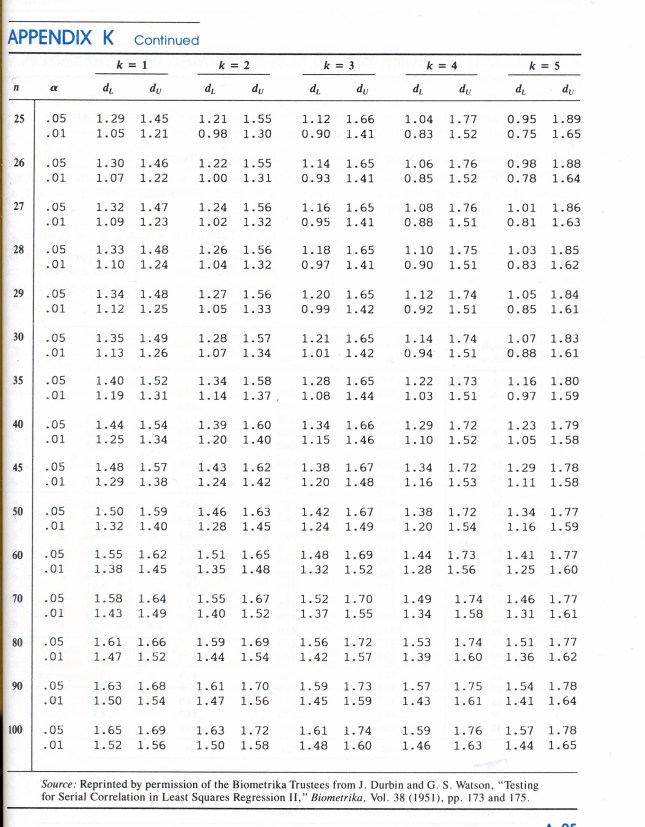
1. Il Correlogramma ed il Test di Durbin-Watson
2. Il Periodogramma del dott. Piero Pistoia

Il modello di Regressione Lineare Semplice (RLS)
1. Prima direzione di ricerca
2. Seconda direzione di ricerca

1. Significato dell’analisi dei residui
2. Stime sulle grandezze della Popolazione

Cenni al significato di media mobile

PARTE 2^a

Analisi della serie storica “ Concentrazione Arsenico”

Metodo delle “Medie Mobili Centrate” – Modello Additivo

Scopo della ricerca
Analisi preliminare e individuazione di outliers
La serie corretta
Gli Effetti Stagionali e la serie destagionalizzata y1t
Il Ciclo-Trend smussato e la componente casuale
Il modello di regressione lineare semplice e test relativi
1. Adeguamento del modello di regressione alla popolazione
2. Il residuo della regressione e l’affidabilità dei tests

4 – Cenni al METODO DELLA MEDIA MOBILE
5 – INIZIO AREA FRA PARENTESI

Programmi utili in R commentati e controllati. Il Correlogramma , la Statistica di Durbin Watson, il Periodogramma (applicato come esercizio a medie trimestrali). Formule trigonometriche delle armoniche costruite dai dati di sfasamento e ampiezza riportati nei risultati.

6 – CENNO A COMANDI DI CALCOLO ED ORGANIZZAZIONE DEI DATI
Filter, matrix e ts di R. Commento sulle prime istruzioni di R (carica dati da file) e processi per automatizzare i ‘conti’
7 – ECCO QUELLO CHE FAREMO CON R: ‘LETTURE’ SUI PROCESSI
8 – INIZIO COPIA SCRIPTS DEL PROGRAMMA CENTRALE
Vari commenti anche difformi e riflessioni anche alternative
9 – PRIMA PARTE IN SINTESI
10 – SECONDA PARTE IN SINTESI
Un altro tentativo sulla caccia ai residui (media mobile 3*3)

11 – L’EPILOGO

EPILOGO

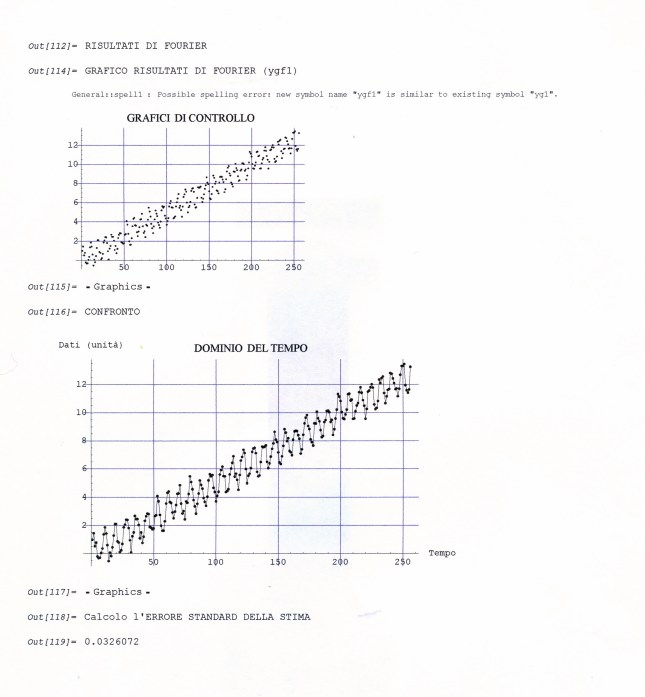
PARTE III^a

^{ULTERIORI APPROFONDIMENTI}

^{1 – APPlICHIAMO UNA REGRESSIONE LINEARE MULTIPLA}

^{1_1 – COME CALCOLARE LA F DI FISHER NELLE RLM ([3] 856-860)}

^{1_2 – COME CALCOLARE L’ERRORE STANDARD (ES) SUI COEFFICIENTI DI REGRESSIONE NELLA RLM}

^{2 – APPLICHIAMO UNA REGRESSIONE MULTIPLA “PESATA”}

^{3 – AZZARDIAMO UNA PREDIZIONE NEL FUTURO}

^{4 – CONCLUSIONI E SUGGERIMENTI}

^BIBLIOGRAFIA

12 -APPENDICE1

Il Correlogramma ed il Test di Durbin-Watson – Lettura Correlogramma

13 -APPENDICE2

PROGRAMMI IN BASIC: calcolo Coefficienti di Autocorrelazione, il Test di Durbin-Watson, il Test della normale di Lin-Mudholkor, analisi spettrale per il Periodogramma. Calcolo dei coefficienti in una regressione multipla (MLR), calcoli con le matrici, metodo di Cholescki. Calcola il radicando dell’errore Standard delle predizioni con la RLM, calcolo matriciale. Tavole per il Test di Normalità di Lin-Mudholkar e per il Test di Durbin-Watson.

14 -APPENDICE3

Tabelle 1-4 dei risultati sull’analisi della serie storica in studio relative all’articolo “Esempi guidati di statistica applicata” di P. Pistoia

15 -APPENDICE4

Analisi con il linguaggio R della serie storica trimestrale rivisitata e ampliata con periodogrammi risultati e grafici.

16 -APPENDICE5

ARTICOLO PREMESSA: “Il senso comune, l’insegnamento scientifico ed i saperi preposti alle scelte” di P. Pistoia

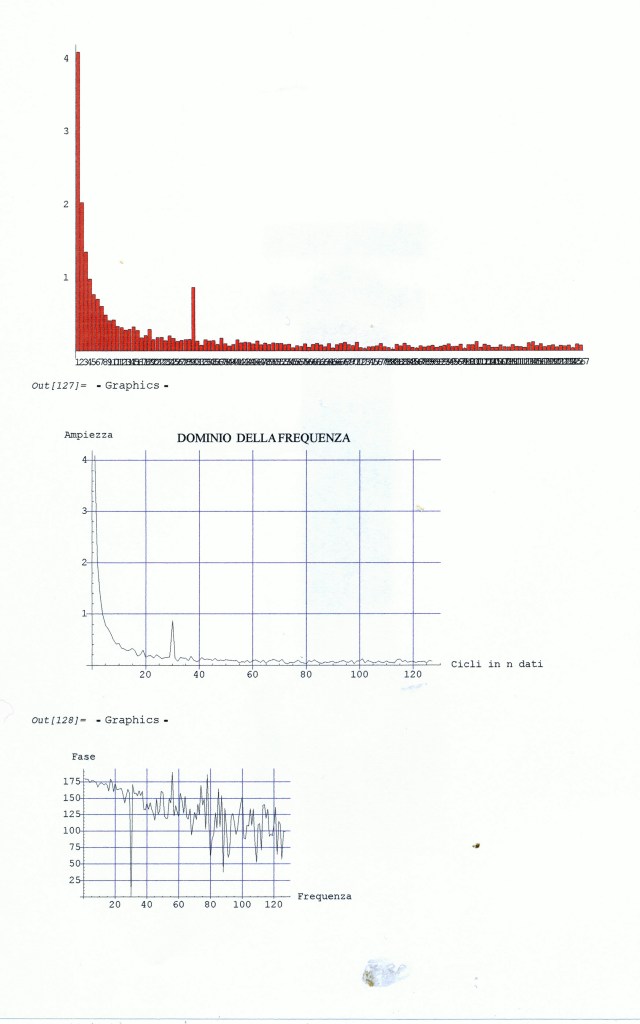
ARTICOLO COMMENTO: “Analisi di Fourier con commenti su dati reali e simulati con il Mathematica di Wolfram vers. 4.2.” di P. Pistoia

“PROGRAMMI in Mathematica con esercitazioni” di P. Pistoia

Vari esempi analizzati compreso ‘Oscillazione mensile ozono a Montecerboli (Pomarance, Pi), 2007,2011’

di Piero Pistoia

L’Esempio 5 si riferisce all’analisi della serie storica concentrazione As detrendizzata.

1 – PREMESSA

PREMESSA SULLO STATO DELL’ARTICOLO

Il presente scritto diventa, sempre più articolato ‘nell’andare’, sempre meno lineare, continuando a riempirsi di parentesi, di alternative informatiche, di pause di riflessione, di ritorni e di correzioni (si veda, per es., il caso del periodogramma come function, ormai praticamente risolto, inseribile come modulo all’interno di qualsiasi programma scritto dai lettori) ecc.. Per me è questo il ‘vero’ articolo scientifico col suo ‘travaglio raccontato (trouble)’, denso di stimoli, possibilità nascoste, interferenze casuali… e non lo scritto finale asettico e razionalmente ripulito, che banalizza il percorso. In questa ottica qualcuno ha detto che l’articolo scientifico è un inganno (Antiseri). Possiamo forse affermare che seguire il ‘processo’ è come un auto-porsi domande-risposte, attraverso una successione di ipotesi-falsificazioni, una sorta di MAIEUTICA SOCRATICA che favorirebbe la costruzione del concetto? Il filosofo non insegna nulla ai discepoli, ma piuttosto a scoprire la ‘verità’, che potenzialmente hanno già dentro di loro (per processo co-evolutivo con la Natura), attraverso una successione di argomentazioni su punti interrogativi. Allora, dal punto di vista educativo-didattico è più importante il percorso o la meta, la storia o l’evento? (meditate, gente, meditate!). Secondo me si apprende molto più e meglio se spingiamo a riflettere sugli errori rilevati, sulle ipotesi a cammino chiuso, sulle falsificazioni insomma, anche in termini di memoria, che seguire acriticamente un racconto lineare, ‘ripianato’, anche se intrinsecamente coerente. In questa disquisizione aperta si inserisce bene anche l’altro aspetto di un Socrate-docente che, perchè ‘ignorante’, costruisce insieme al discepolo, senza conoscenze preacquisite (risuonano qui le posizioni di Foerster e Bruner, da richiamare in questo blog).

Per sovrapporre però una ‘lettura’ su video meno discontinua e difficile, che serva come back-ground, una guida all’apprendimento più lineare, più conforme, meno a ‘frullato di pezzi di concetti’ e quindi forse più facile e più gradevole, trasferiamo, col titolo ‘IL PROLOGO’, la prima parte dell’articolo originale dello stesso autore (senza l’uso di R, ma di scripts in Qbasic ed Excel), di cui lo scritto in questione voleva essere una ‘lettura rivisitata’ mediata dal linguaggio R e dal Mathematica di Wolfram. Prima delle appendici trasferiamo anche la seconda parte col titolo ‘L’EPILOGO’. L’intenzione è introdurre all’inizio anche un INDICE a link per migliorare l’accesso alle diverse ‘zone mosaico’ dell’articolo. Mi scuso per ‘questo andare’ poco controllato! Se mi rimanesse più energia mentale e ‘tempo di vita’ forse potrei anche rivisitarlo.

Comunque, un buon apprendistato sarebbe quello di leggere, prima di questo intervento, il primo post dal titolo “Un percorso verso il periodogramma” curato dallo stesso autore. Grazie.

2 – IN ANTEPRIMA

IN ANTEPRIMA

ECCO LA FUNCTION PRDGRAM DEL PERIODOGRAMMA IN R scritto dal dott. Piero Pistoia

FUNZIONE DEL PERIODOGRAMMA in pdf OK:

FUNZIONE DEL PERIODOGRAMMA1-P_Pistoia

ATTENZIONE!

Segue una proposta di esercitazione da attivare sulla consolle di R: 1) si incolla la f. PRDGRAM in R e in successione 2) si trasferiscono gli ESERCIZI dell’esercitazione, per es., uno alla volta. Si hanno i dati e grafici in uscita per ogni ESERCIZIO. Ricordarsi, una volta sulla consolle, per prima cosa, sempre azzerare i dati, che R ha già in memoria, tramite il menù ‘VARIE’ (Rimuovi tutti gli oggetti) e poi introdurre in R, prima di incollare la PRDGRAM, le ‘library’ necessarie (tseries e graphics).

Per vedere in pdf l’Esercitazione cliccare sotto:

periodogramma-_di_dati_simul-trend_random_mod2_3 (2)

0ppure……. continuare a leggere…….


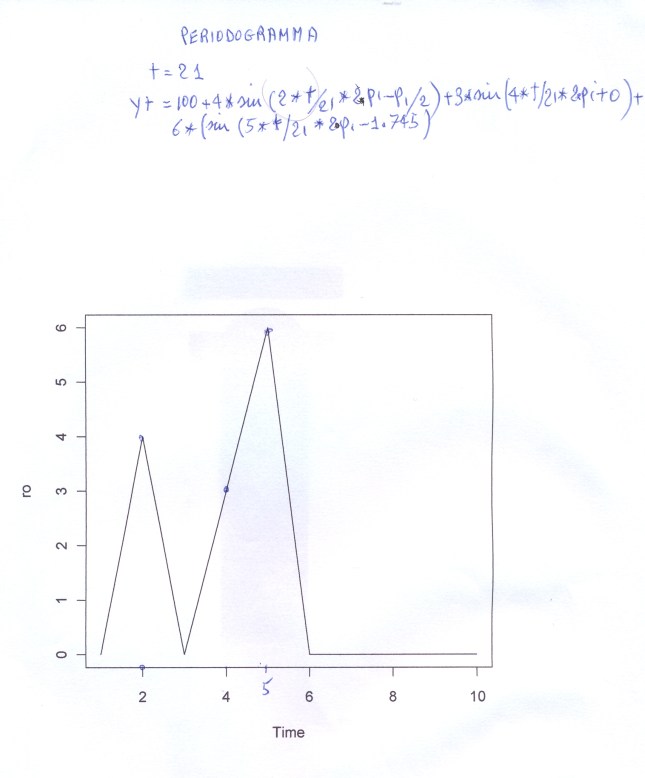
PROPOSTA DI ESERCITAZIONE ANCHE PER FAVORIRE L'ACQUISIZIONE 
INTUITIVA DELLA 'LETTURA' DI UN PERIODOGRAMMA (contenuta nel 
precedente link) di Piero Pistoia

Inizialmente vogliamo simulare ad hoc una serie storica 
'tabellando' n=21 dati da tre funzioni del seno con costante 
additiva 100,con ampiezze rispettivamente 4,3,6 e 'frequenze' 
nell'ordine 2/21, 4/21,5/21 e infine  fasi -pi/2, 0, -1.745, 
con  il comando iniziale di di R: t=c(1:n), usando come base 
per i nostri esempi proprio questa espressione:
 
yt=100+4*sin(2*pi*2*t/n-pi/2)+3*sin(2*pi*4*t/n+0)+
6*sin(2*pi*5*t/n-1.745) #0.

Calcolati i 21 dati yt, attribuendo a t valori da 1 a 21 
nell'espressione precedente, tali dati rappresentano 
proprio lanostra serie storica da sottoporre al 
Periodogramma, una volta precisati i tre valori 
essenziali da passare ad esso (yt,n,m), dove m è il 
numero di armoniche da calcolare; m=n/2-1 se n è 
pari; m=(n+1)/2 se m è dispari. 
Tramite il nostro programma in R calcolammo allora 
i valori di ampiezze e fasi per le prime 10 armoniche 
riscoprendo nei dati le oscillazioni che c'erano.
Per esercizio continuiamo a simulare serie storiche 
modificandol'espressione di base, modificandola anche 
aggiungendo, a scelta, un trend lineare (k*t) e/o 
valori random onde controllare se il Periodogramma 
riesce a"sentire", oltre alle oscillazioni armoniche, 
anche il trend e la componente casuale.
Con l'istruzione '#' elimineremo secondo la necessità 
le linee di programma non utilizzate per lo scopo 
prefissato.
	 
Proviamo, prima, ad applicare il programma su 21 dati 
simulati dalle espressioni di una retta inclinata e da 
una serie random estratta da una distribuzione gaussiana. 
Sceglieremo poi una combinazione di seni interessanti 
più adatta a proseguire l'esercitazione.  



PERCORSI DA INVESTIGARE
 
par(mfrow=c(1,1))

 #n=21
 #n=240
			
 #t=c(1:n)
 
 # yt=0.5*t # 1
 #si tratta di un ramo di iperbole(?)discendente
 
 #yt=c();yt[1:t]=0
 
 #yt <- rnorm(t,0,1) # 2
 #yt=-4+ 0.5*t + rnorm(t,0,1) # 3
 
#yt=100+4*sin(2*pi*2*t/256-pi/2)+3*sin(4*t/256*2*pi+0)+
6*sin(5*t/256*2*pi-1.745) # 4 
#analisi yt; tenendo come base questa espressione con 
armoniche basse, ro è sulla rampa alta #della 'iperbole' 
e si obnubila il trend.
 
 #yt=100+4*sin(2*pi*2*t/n-pi/2)+3*sin(2*pi*4*t/n+0)+
6*sin(2*pi*5*t/n-1.745) + 0.1*t # 5 
 
#analisi yt_reg
 
 #yt=100+2*sin(2*pi*2*t/n-pi/2)+sin(2*pi*4*t/n+0)+
3*sin(2*pi*5*t/n-1.745) + rnorm(t,0,1)*2 # 6 
 #analisi yt_rnorm: diminuiamo le ampiezze e aumentiamo 
i random
 
 #yt=100+4*sin(2*pi*2*t/n-pi/2)+3*sin(2*pi*4*t/n+0)+
6*sin(2*pi*5*t/n-1.745) + 0.5*t)+(rnorm(t,0,1)-1/2))  # 7 
 #analisi yt_reg_rnorm

 yt <- 6*sin(2*pi*5*t/n)+2*sin(2*pi*30*t/n)+ 
3*sin(2*pi*40*t/n)+0.1*t + rnorm(n,0,1)*2 # 8 

 #questa espressione anche con 'frequenze' alte (30,40) è la 
 #più indicata a dimostrare che il Periodogramma 'scopre' anche trends 
 #e randoms oltre alle oscillazioni sinusoidali.
 
Ora possiamo prevedere che cosa accade se togliamo una 
o due di queste tre,basta far girare il programma nei 
diversi casi. 
 In questo contesto nel prosieguo useremo invece, per 
esercizi, le tecniche di scomposizione di una serie 
storica: proviamo a 'destagionalizzarla' in successione 
con due o tre medie mobili opportune (o magari col 
comando filter di R) per controllare che cosa rimane 
(che cosa accade ai random?). Potevamo anche 
'detrendizzarla prima con una regressione lineare, 
ovvero eliminare i random con una media mobile 3*3 ecc..


TRACCIA DEI PERCORSI

ESERCIZIO N° 0

n0=256 # può essere cambiato
t=c(1:n0)
yt0=100+4*sin(2*pi*2*t/n0-pi/2)+3*sin(2*pi*4*t/n0+0)+
6*sin(2*pi*5*t/n0-1.745)
yt0 # la serie storica
ts.plot(yt0)
if(n0/2==n0%%2) m0=n0/2-1 else m0=(n0-1)/2
yt0_period=PRDGRAM(yt0,n0,m0)
yt0_period # data in uscita con ampiezza e fase, per il 
controllo
yt0_period$ro # vettore delle ampiezze
ts.plot(yt0_period$ro)

Esercizio N° 1

n01=21
t=c(1:n01)
yt1=0.5*t
yt1 # serie storica
ts.plot(yt1)
if(n01/2==n01%%2) m01=n01/2-1 else m01=(n01-1)/2
yt1_period=PRDGRAM(yt1,n01,m01)
yt1_period #data in uscita comprese ampiezze e fasi
yt1_period$ro #vettore delle ampiezze
ts.plot(yt1_period$ro)

Esercizio N° 2

n2=21 # può essere cambiato
t=c(1:n2)
yt2<- rnorm(t,0,1)
plot(yt2)
yt2 # serie storica
if(n2/2==n2%%2) m2=n2/2-1 else m2=(n2-1)/2
yt2_period=PRDGRAM(yt2,n2,m2)
yt2_period # data in uscita
yt2_period$ro # vettore delle ampiezze
plot(yt2_period$ro)

ESERCIZIO N° 4

n4=256 # può essere cambiato
t=c(1:n4)

yt4=100+4*sin(2*pi*2*t/256-pi/2)+3*sin(2*pi*4*t/256+0)+

6*sin(2*pi*5*t/256-1.745)
yt4 
ts.plot(yt4)
if(n4/2==n4%%2) m4=n4/2-1 else m4=(n4-1)/2
yt4_period=PRDGRAM(yt4,n4,m4)
yt4_period # data in uscita
yt4_period$ro # vettore delle ampiezze
ts.plot(yt4_reg$ro)




ESERCIZIO N° 5

n5=256 # può essere cambiato
t=c(1:n5)

yt5=100+4*sin(2*pi*2*t/256-pi/2)+3*sin(2*pi*2*pi*4*t/256+0)+

6*sin(2*pi*5*t/256-1.745)-0.1*t

plot(yt5,type=”l”)
if(n5/2==n5%%2) m5=n5/2-1 else m5=(n5-1)/2
yt5_reg=PRDGRAM(yt5,n5,m5)
yt5_reg # data in uscita
yt5_reg$ro # vettore delle ampiezze
ts.plot(yt5_reg$ro)
                               ____________________________________________

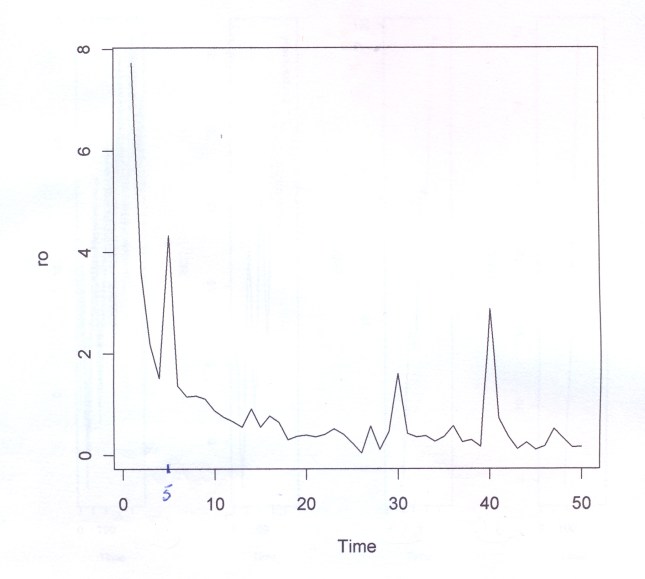ESERCIZIO N° 8
par(mfrow=c(1,2))

n8=100 # può essere cambiato
t=c(1:n8)

yt8=6*sin(5*pi*2*t/n8-pi/2)+2*sin(2*pi*30*t/n8+0)+3*sin(2*pi*40*t/n8-1.745)+rnorm(n8,0,1)*2

ts.plot(yt8)
if(n8/2==n8%%2) m8=n8/2-1 else m8=(n8-1)/2
yt8_reg=PRDGRAM(yt8,n8,m8)
yt8_reg # data in uscita
yt8_reg$ro # vettore delle ampiezze
ts.plot(yt8_reg$ro)

GRAFICO YT8 E PERIODOGRAMMA (Yt8_reg$ro) SENZA IL TREND

GRAFICO DI Yt8_reg_rnorm n=240


 

GRAFICO Yt8  ANCHE CON IL TREND (serie originale)
 
 
#RIFLESSIONI
#Se aggiungo il trend 0.1*t a yt8 ottengo il grafico 
precedente. Confrontando il grafico che segue#e quello 
precedente sarebbe interessante approfondire 
intuitivamente perché col trend le ampiezze
#vengono disturbate tanto più quanto più lentamente 
scende a zero il ramo di 'iperbole'.Sembra #quasi così, 
induttivamente, si possa affermare la regola empirica 
(ipotesi) che armoniche con #frequenze più alte  vengano 
disturbate meno di quelle più basse, che si posizionano 
sul ramo a #pendenza più elevata e con i suoi punti 
più distanti dall'ascissa. Se sommiamo la distanza della 
#base dei picchi dall'asse orizzontale alla cima dei 
picchi l'ampiezza tenderebbe al valore della 
#formula? Se togliamo anche i random da yt8 i tre picchi 
sarebbero poggiati sull'asse orizzontale?#La numerosità 
di yt8 influisce o no sulla velocità con cui si muove 
verso l'asse x la curva del  trend? Cercare di rispondere 
osservando i grafici precedenti.

FINE ANTEPRIMA

<A NAME=”punto3″>IL PROLOGO

IL PROLOGO

3 – PROLOGO

COME INTRODUZIONE RIPORTIAMO LA PRIMA PARTE DELLA RICERCA ORIGINALE (SENZA L’USO DI R); LA SECONDA PARTE VIENE RIPORTATA PRIMA DELLE APPENDICI.

SE VUOI APPROFONDIRE LE PROBLEMATICHE RELATIVE A FOURIER VEDI L’APPENDIX5

LA COSTRUZIONE SI FA CON L’ANDARE!

LA FUNCTION DEL PERIODOGRAMMA ora può essere trasferita come modulo in qualsiasi altro programma scritto da chiunque! Abbiamo cercato di correggere tutti gli scripts dove figurava questa funzione all’interno di questo post. Vedere di seguito (area definita “fra parentesi”) il funzionamento di un listato con svariati richiami a questa funzione con proposte di ‘gioco’ con le armoniche su una serie storica reale (serie storica trimestrale) …. Il listato del periodogramma è lungo e articolato. Nell’analisi di una serie di dati storici con piu’ serie derivate capita spesso di far uso di questo listato per guardare all’interno delle serie. E’ pertanto utile riuscire a scrivere una sola volta questo listato per poi richiamarlo quando serve. Da riorganizzare anche testo e paragrafi. Problemi sorgono anche perché R memorizza all’uscita tutti gli oggetti su cui ha lavorato che tacitamente, pur nascosti, sono ancora disponibili. Questi valori possono interagire sui programmi in via di sviluppo, creando situazioni le più disparate. In generale conviene dal menù ‘varie’ eliminare questi valori prima di far girare o costruire programmi! Si cercherà con calma di attivare i controlli anche sugli altri post, dove figura la function PRDGRAM.

ATTENZIONE: I SEGMENTI DELL’ARTICOLO IN GRIGIO CHIARO HANNO UNA BARRA ORIZZONTALE IN FONDO PER MUOVERE LO SCRITTO A DESTRA E SINISTRA, SE LO SCRITTO ESCE DALLO SCHERMO

FINE PROLOGO

UN PARZIALE PERCORSO DI BASE SULL’ANALISI STATISTICA DI UNA SERIE STORICA REALE POCO INTUITIVA COMMENTATO CON IL LINGUAGGIO R

“Letture” su concetti statistici e su alcuni aspetti della programmazione

Dott. Piero Pistoia

PREMESSA

NB – I GRAFICI OTTENUTI CON IL SUPPORTO DEL PROGRAMMA CORR IN QBASIC (ALLEGATO) E DI EXCEL, SE RIUSCIAMO A RIDISEGNARLI TUTTI, FACENDO GIRARE GLI SCRIPTS DEL LINGUAGGIO R CHE SEGUONO, QUESTO E’ UN EFFICACE CONTROLLO INTERNO ALLO SCRITTO.

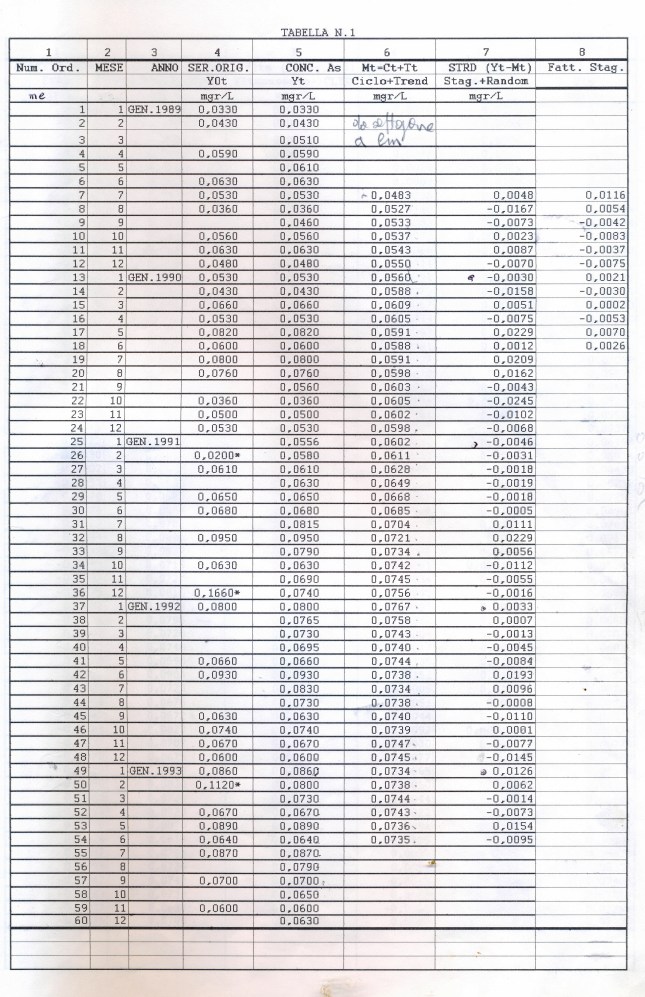
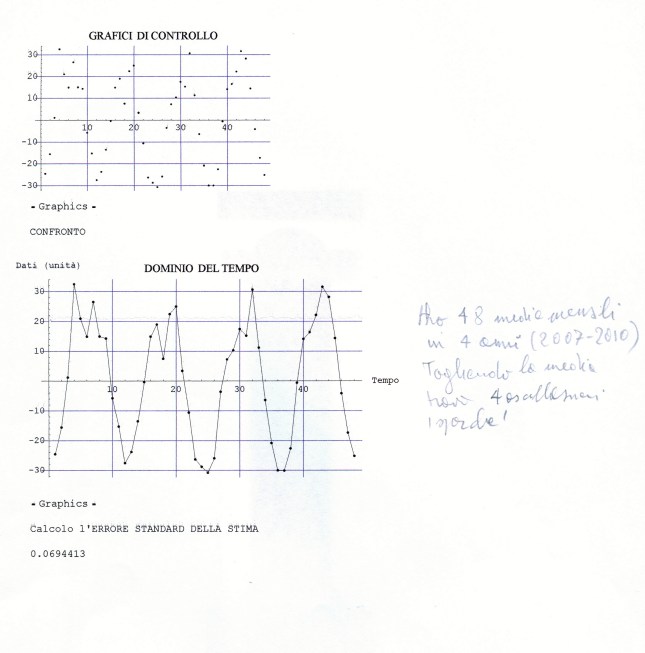
Il file.dati che prenderemo come campione da analizzare riguarda le concentrazioni mensili di arsenico (As) misurate in mg/l nelle acque della Carlina (sorgenti Onore), prov. Siena, nell’intervallo di tempo 1989- 1993 (5 anni, 60 mesi con inizio da gennaio). Dopo interpolazione per i dati mancanti, un’analisi preliminare (Modello Additivo secondo il Metodo delle Medie Mobili Centrate) porta ad individuare tre residui standardizzati elevati (> 2 in valore assoluto e quindi considerati outliers da eliminare e sostituire con nuova interpolazione,ottenendo così una serie storica corretta, stocastica e discreta; stocastica, nel senso che il futuro è solo parzialmente determinato dai valori del passato e discreta, nel senso che le misure sono fatte in tempi specifici (ogni mese) a uguali intervalli.

Su questa serie (yt=as1) di 60 dati – inserita nel file che si chiama As-Carlina1.csv – e che comunque verrà esplicitata all’inizio dell’analisi – procediamo “a fare i conti” e a gestirla con R. Questa parte iniziale preliminare verrà trattata successivamente.

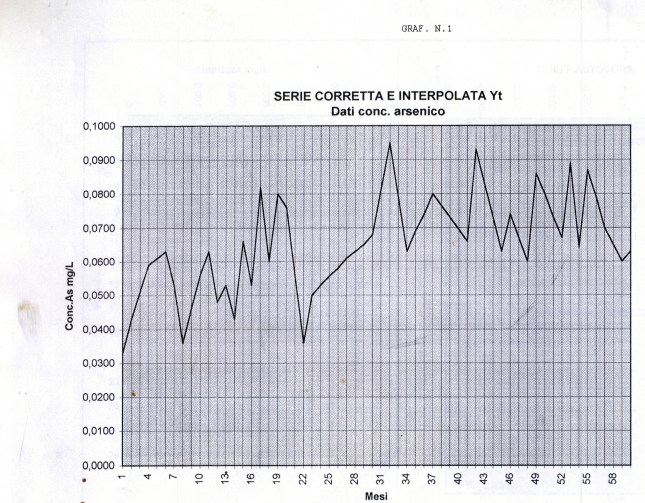
Intanto alleghiamo di seguito Il grafico della serie corretta e interpolata (Graf. N.1).

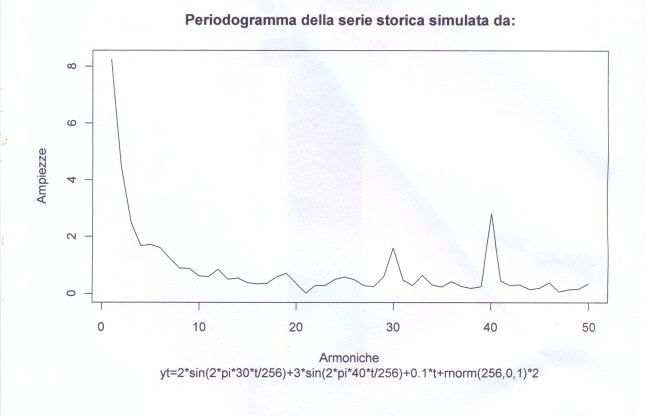
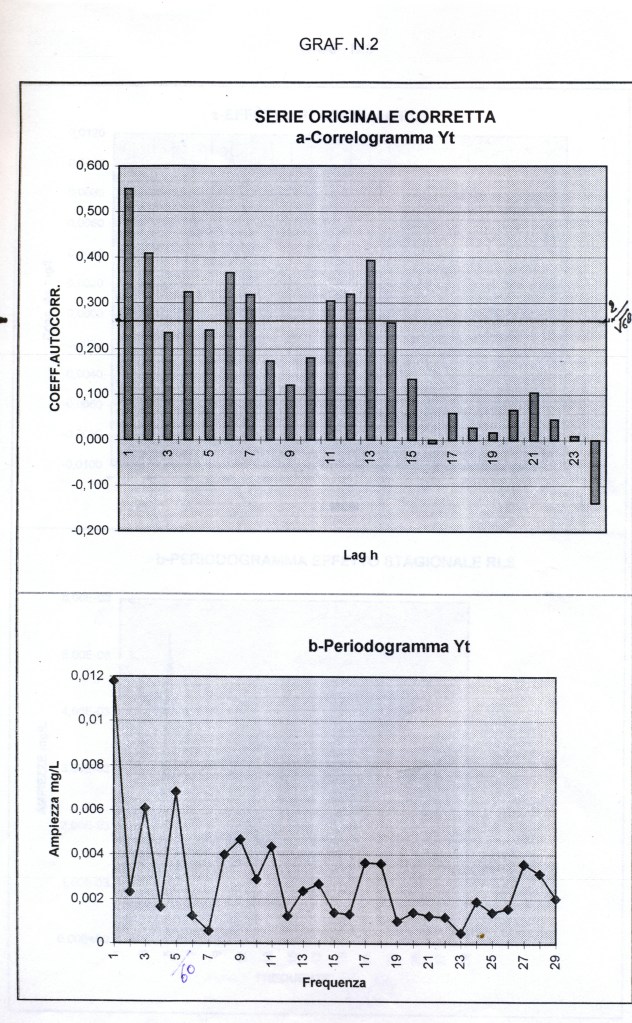
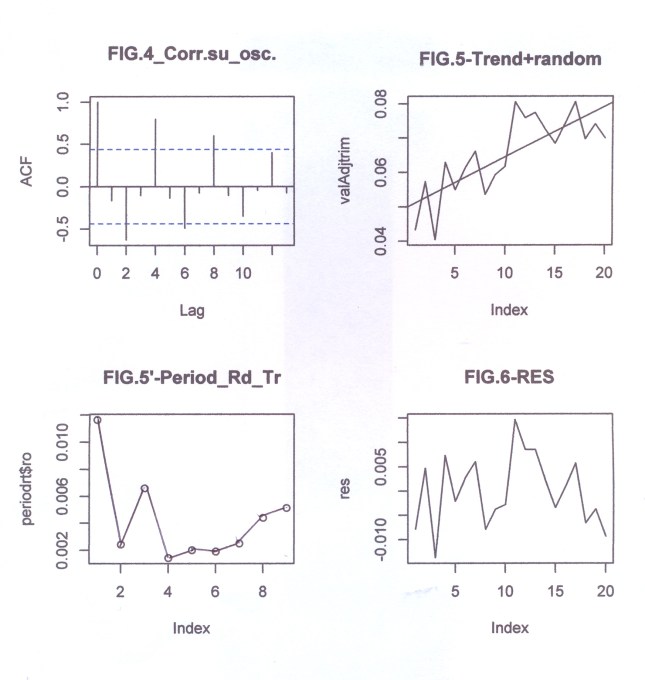
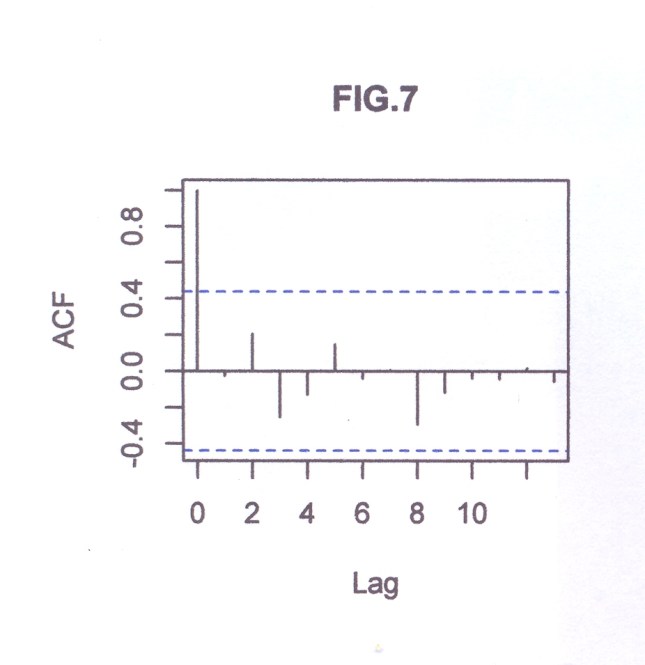
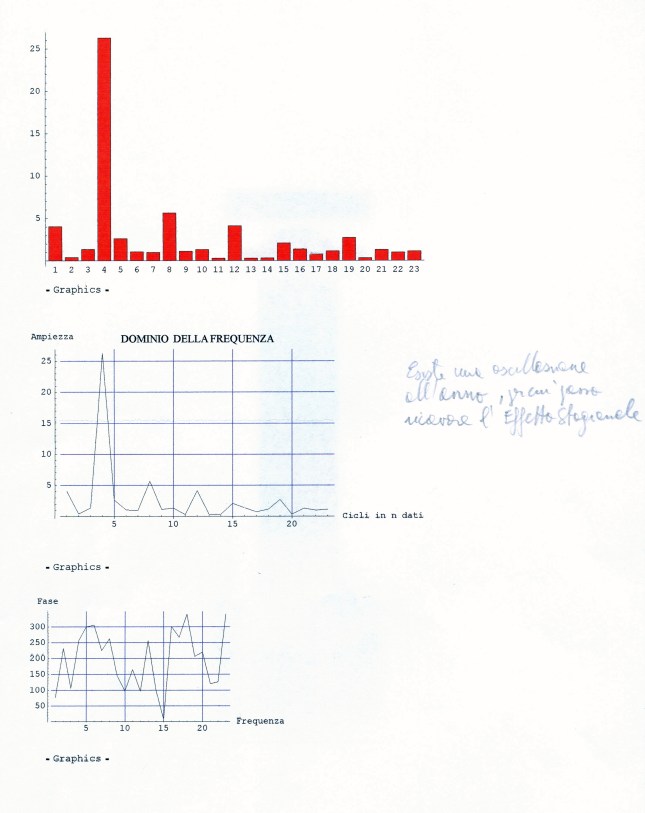
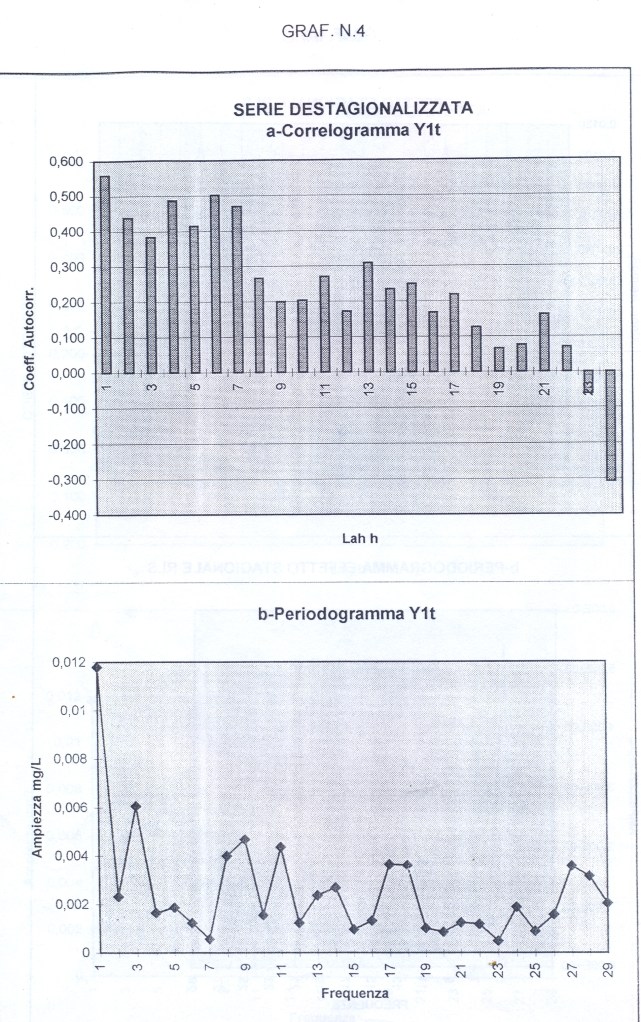
L’analisi di base di una serie storica procede alla ricerca delle uniformità al suo interno, come TREND, vari tipi di stagionalità periodica (giornaliera, settimanale, mensile, trimestrale ecc.) correlata al carattere dei dati che abbiamo (orari, giornalieri, settimanali,ecc.), cicli con eventuale periodo superiore che esce dal range dei dati (in generale periodo e ampiezza variabili), la componente random, che riassume lo ‘white noise’ ed altro (impulsi erratici). Alleghiamo come informazioni preliminari anche il relativo grafico dell’autocorrelogramma e del periodogramma (GRAF. N. 2, a e b). Si rimanda al loro significato e processo alla Appendice 1 di questo articolo e al Post scritto a nome di P.Pistoia ed altri, facilmente accessibile da questo sito, per es., battendo periodogramma nella finestra ‘Cerca’. Anticipiamo che dal correlogramma (GRAF. N.2 a) si osservano una stretta convessità intorno al valore 12-13 che supera la fascia dell’errore, una ondulazione dei picchi (forse una oscillazione), un permanere di picchi nella zona positiva (TREND) ed altro e quindi si evince che i dati della serie al 95% di fiducia, non sono random e dal periodogramma si nota un picco forse rilevante corrispondente al valore 5 (5 oscillazioni nel range dei dati, cioè 5 oscill. in 5 anni, una oscillazione all’anno, quindi periodo=12 mesi). In dati mensili, una oscillazione periodica di periodo 12 è allora un’ipotesi plausibile.

Scegliamo di procedere, come tentativo, per prima cosa ad eliminare dalla serie storica corretta ( yt o as1) l’oscillazione stagionale prevista dai grafici precedenti. Useremo vari metodi per farlo e confronteremo poi i risultati.

4 – Cenni al METODO DELLA MEDIA MOBILE

SINTESI SUL METODO DELLA MEDIA MOBILE

Il metodo della media mobile consiste nel sostituire ai valori osservati, valori artificiali corretti, ottenuti effettuando la media di ciascun valore con quelli contigui (per il calcolo vedere, per es., [3] pag. 997), ottenendo una nuova serie storica.

Se da una serie storica vogliamo eliminare una oscillazione di un dato periodo, bisogna scegliere, per il calcolo della media, una lunghezza del periodo mobile uguale il più possibile alla lunghezza del periodo dell’oscillazione prevista.

E’ da tener presente che sembra che talora tale metodo abbia il difetto di inserire un ciclo fittizio in una serie storica anche casuale. Abbiamo controllato nel caso della serie trimestrale enucleata da quella in studio (vedere dopo).

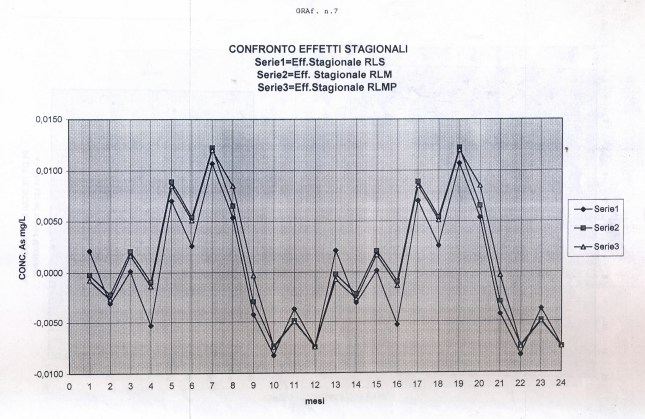
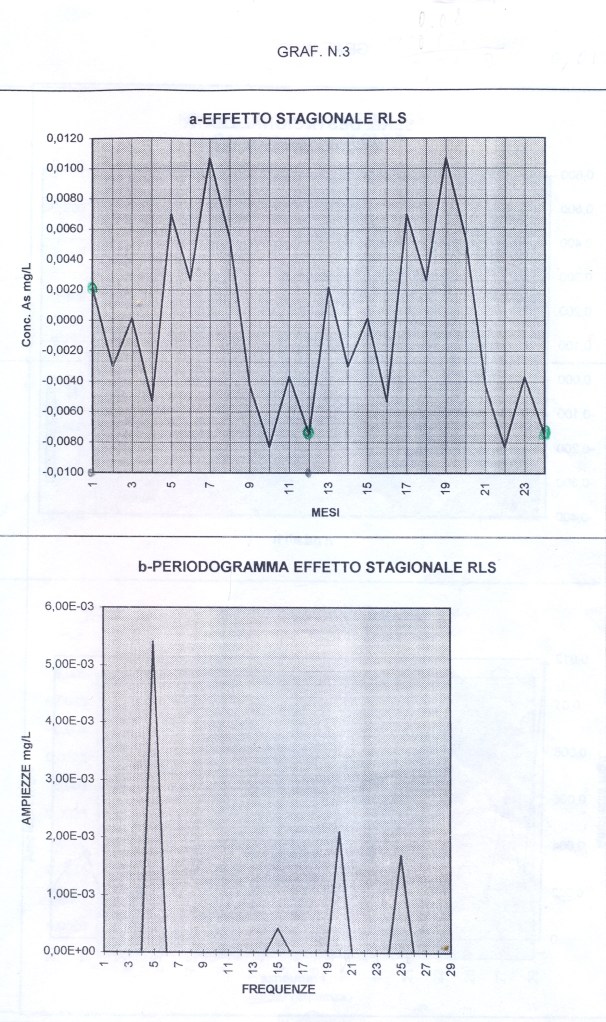
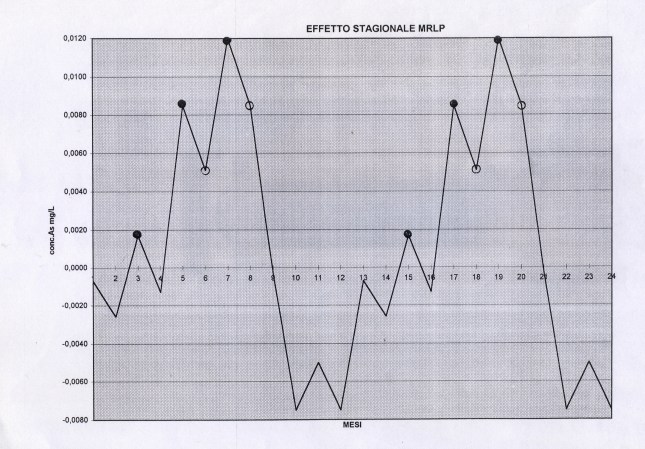
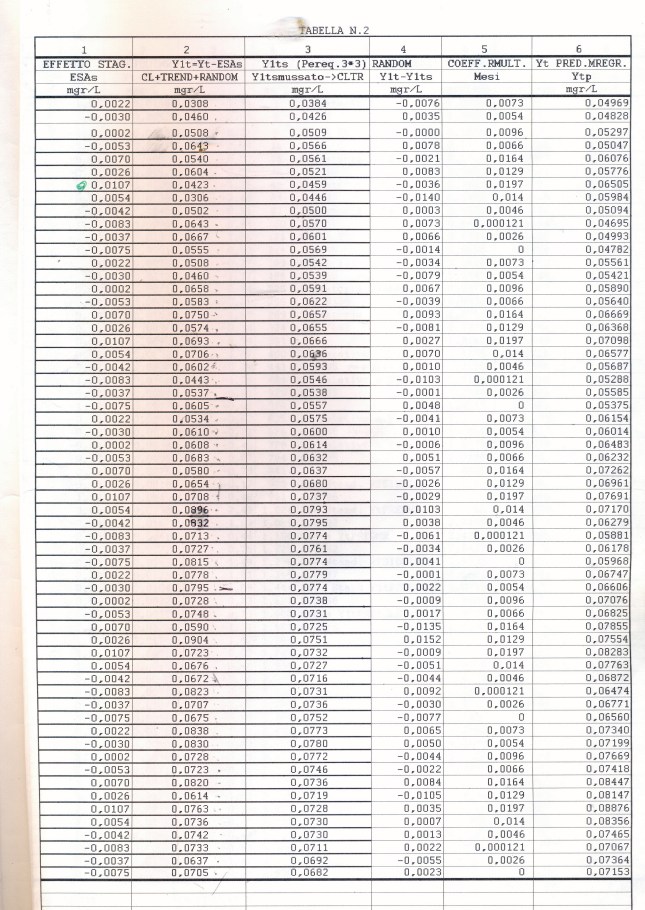
Useremo la Media Mobile Centrata di ordine 12 (come suggerito dai grafici preliminari) che di norma elimina l’oscillazione di uguale periodo insieme alle componenti casuali dalla serie originale, trasformando la serie mensile originale (yt o as1, che inizia con gennaio, APPENDIX3, TABELLA N.1, col.5 ) in una serie storica di dodici termini più corta (la serie Mbt, APPENDIX3, TABELLA N.1, col.6, che perde i valori dei primi sei mesi e degli ultimi sei, e inizia da luglio). Da porre attenzione che nel processo di scorciamento il primo termine della serie Mbt si riferisce al mese di luglio del primo anno e così via. L’Mbt sottratta da quella originale (as1) ne fornisce una della stessa lunghezza della precedente (48 temini), l’STRD (componente stagionale + random, APPENDIX3, TABELLA N.1, col.7 ), sulla quale operiamo poi per ottenere il Fattore Stagionale costituito da dodici termini, uno per ogni mese (oscillazione in un anno). Per ottenere il Fattore Stagionale corrispondente ad un mese, si considerano tutti i valori della serie STRD (più corta di 12 termini) corrispondenti a quel mese e se ne fa la media. Quando faremo girare il programma scritto con R e vedremo i 48 valori della serie STRD, potremo controllare che, per es., i 4 valori del mese di gennaio (il settimo, il diciannovesimo, il trentunesimo, il quarantaduesimo) sono -0.0030, -0.0046, 0.0033, 0.0126 e facendo la media otterremo il 7° elemento del Fattore Stagionale, 0.0022, cioè il primo elemento di ESAs (APPENDIX3, TABELLA N.2, col.1), EFFETTO STAGIONALE, la cui oscillazione è visibile nel GRAF. N.3 a.

Così per il mese di gennaio si fa la media dei 4 valori di gennaio contenuti nella serie STRD, ottenendo il primo valore dell’Effetto e così via. Con questi processi di media verranno eliminate anche le componenti casuali, se ci sono rimaste, dalla serie STRD che diviene così ST (stagionalità). Ripetendo 5 volte la ST copriamo i 5 anni, ottenendo l’Effetto Stagionale. E’ necessario però prima riorganizzare i 12 termini del Fattore Stagionale, spostando i primi sei termini, alla fine degli ultimi sei in maniera da avere i 12 valori allineati da gennaio a dicembre. Per il controllo di questa oscillazione applichiamoci, per es., il programma CORR scritto in Qbasic dall’autore (nota 2) o in linguaggio R (vedere sotto PARENTESI) e focalizziamo l’attenzione sul periodogramma dell’ultima serie ottenuta per osservare la frequenza di questa oscillazione (GRAF. N.3 a,b dell’Effetto Stagionale, ottenuto invece per mezzo di Excel): chiaramente significativa appare la frequenza 5. Troveremo lo stesso periodogramma anche con R. Con R useremo la funzione acf (file, main=”Titolo”), per ritrovare i correlogrammi costruiti con CORR ed excel; per il periodogramma si rimanda anche alla relativa routine qui riproposta, rivisitata e funzionante.

————————————————-

5 – INIZIO AREA FRA PARENTESI

5-AREA FRA PARENTESI

APERTA PARENTESI

Alcuni programmi in R utili nello studio delle serie storiche

Da notare (fra parentesi) il programmino riportato qui sotto, scritto in linguaggio R dal sottoscritto, con i suoi risultati, che calcola egregiamente (almeno sembra) i coefficienti di auto-correlazione di una serie storica di prova:

y=c((1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20)). Comunque, nell’andare, lo vedremo in azione per i tanti confronti e prove! Si aggiungono di seguito anche scripts in R per il calcolo di DW (test di Durbin Watson), metodo più efficace nell’analisi dei correlogrammi, sempre del sottoscritto.

ATTENZIONE! GLI SCRIPTS DEI PERIODOGRAMMI COME SUBROUTINES (functions) SONO IN VIA DI CORREZIONE

RIPORTIAMO SUBITO ANCHE IL PROGRAMMA PIU’ COMPLESSO PER COSTRUIRE IL PERIODOGRAMMA DI UNA SERIE STORICA con i relativi risultati per il controllo . Un controllo quantitativo più puntuale è stato condotto col MATHEMATICA 4.2 di Wolfram nella APPENDIX4 (Piero Pistoia)

Queste routines messe sotto forma di Functions serviranno per costruire correlogrammi, tests di DW e periodogrammi ognivolta che servono.

library(tseries)

# PROGRAMMINO ‘CORRELOGRAMMA’

# Un piccolo strumento per allenare anche l’intuito

#dott. Piero Pistoia

result=c() # result=c(NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA)
result1=c() # result1=c(NA,NA,NA,NA,NA,NA,NA,NA,NA,NA)
#y=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20)
y=c(1:20) 
# Il lettore può a piacere aggiungere altre funzioni (anche numeri casuali), tentare di indovinare # con ipotesi e poi controllare, per acquisire intuizione sul Correlogramma e sui suoi limiti.

#Controllare se le definizioni dei vettori con elementi NA sono necessari! Sembra di no!
#y=c(1,2,3,4,5)
 N=length(y)
 m=10
 yM=mean(y)

 for(h in 1:m){
for (t in 1:N-h){
 result[t]=(y[t]-yM)*(y[t+h]-yM)
 }
result1[h]=sum(result)
} # OK
result1
result2=c()
#result2=c(NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA)
#for(h in 1:m){

 for(t in 1:N){
 result2[t]=(y[t]-yM)^2
 }
result3=sum(result2)

# Calcolo il coeff. di correl. di lag 1

rh=result1/result3

t=seq(1:10)

Prh=plot(t,rh)

RISULTATI DELLA PROVA (nessun errore rilevato dalla consolle di R nella prima prova!)

> load(“C:\\Users\\Asus\\Documents\\.RData”)
> library(tseries)

‘tseries’ version: 0.10-32

‘tseries’ is a package for time series analysis and computational
finance.

See ‘library(help=”tseries”)’ for details.

> result=c(); result=c(NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA)
> result1=c(); result1=c(NA,NA,NA,NA,NA,NA,NA,NA,NA,NA)
> y=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20)
>
> #y=c(1,2,3,4,5)
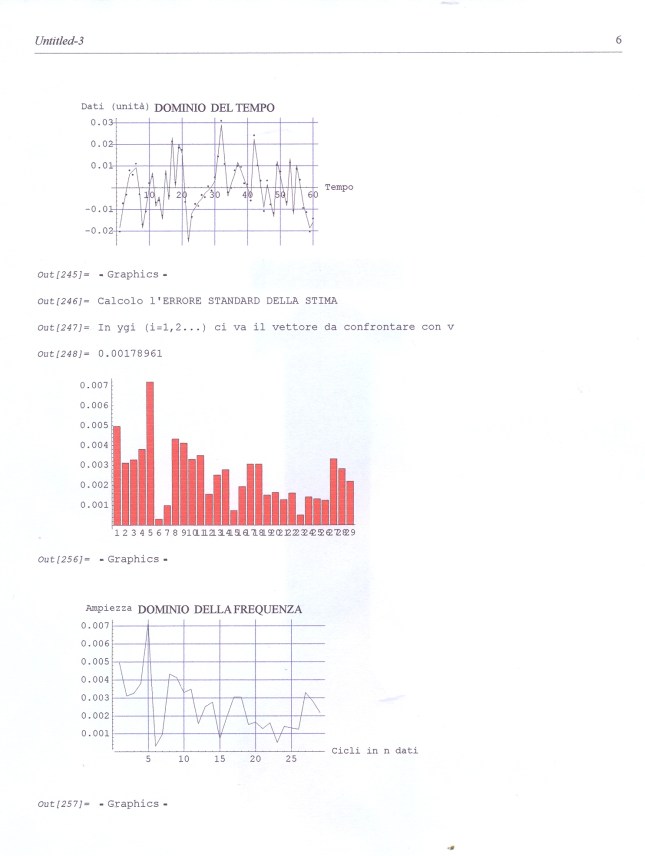
> N=length(y)
> m=10
> yM=mean(y)
>
> for(h in 1:m){
+ for (t in 1:N-h){
+ result[t]=(y[t]-yM)*(y[t+h]-yM)
+ }
+ result1[h]=sum(result)
+ } # OK
Ci sono 45 avvisi (usare warnings() per leggerli)
> result1
[1] 565.25 385.75 233.75 107.25 4.25 -77.25 -139.25 -183.75 -212.75
[10] -228.25
>
> result2=c(NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA)
> #for(h in 1:m){
>
> for(t in 1:N){
+ result2[t]=(y[t]-yM)^2
+ }
> result3=sum(result2)
>
> # Calcolo il coeff. di correl. di lag 1
>
> rh=result1/result3
>
> t=seq(1:10)
>
> Prh=plot(t,rh)

Risultato da confrontare con acf(y)

SE SCRIVIAMO coeffcorr=acf(y), R DARA’ ANCHE IL VETTORE DATI IN coeffcorr

La formula usata è quella senza la moltiplicazione per N/(N-1)

LA STATISTICA DI DURBIN WATSON

library(tseries) 
y=c(1,2,3,4,5,6,7,8,9,10) 
n=length(y) 
#result=c(NA,NA,NA,NA,NA,NA,NA,NA,NA)
 result=c()
 result1=c()
for(t in 2:n){
 result[t]=(y[t]-y[t-1])^2
}
result=result[2:n]
a=sum(result)

for(t in 1:n)
result1[t]=y[t]
b=sum(y)
dw=a/b
dw

#Nella tabella, k'=n° regressori non contando la costante, a=n° osservazioni (y) e dw, sono le tre informazioni per fare il 
test con la tabella.
#Per k'=1 e a=20  l'intervallo dl-du=1.201-1.411, per cui 0.2 < dl:  presenza di correlazione,
#si respinge l'ipotesi nulla (ipot. nulla = i dati non sono 
correlati!), come era intuitivamente già nelle cose.
Da notare che normalmente il test si applica ai residui per 
testare la loro indipendenza.

RISULTATI DELLA PROVA (nessun errore sulla consolle di R) 
> library(tseries) 
> y=c(1,2,3,4,5,6,7,8,9,10) 
> n=length(y) > 
#result=c(NA,NA,NA,NA,NA,NA,NA,NA,NA) 
> result=c() > result1=c() 
> for(t in 2:n){ + result[t]=(y[t]-y[t-1])^2 + } 
> result=result[2:n] 
> a=sum(result) 
> > for(t in 1:n) 
+ result1[t]=y[t] 
> b=sum(y) 
> dw=a/b 
> dw [1]
 0.1636364
 >

#TENTIAMO SCRIPTS del PERIODOGRAMMA IN FORMA DI FUNCTION del dott. Piero Pistoia

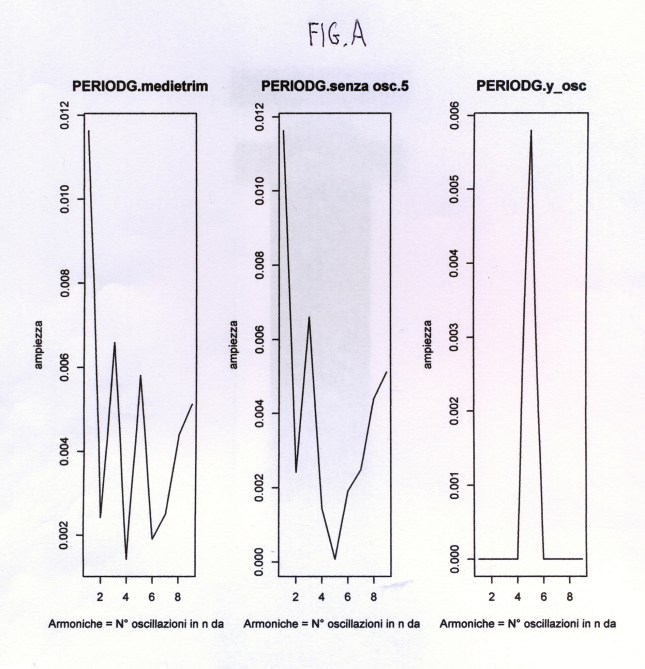
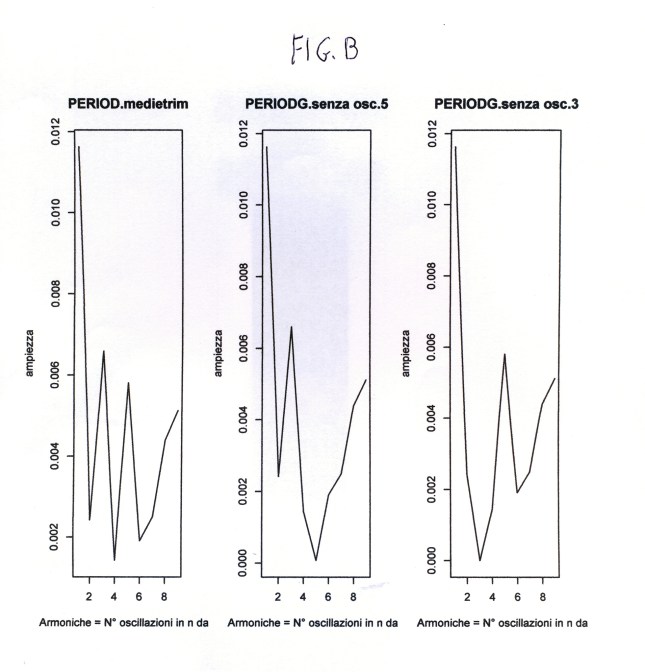
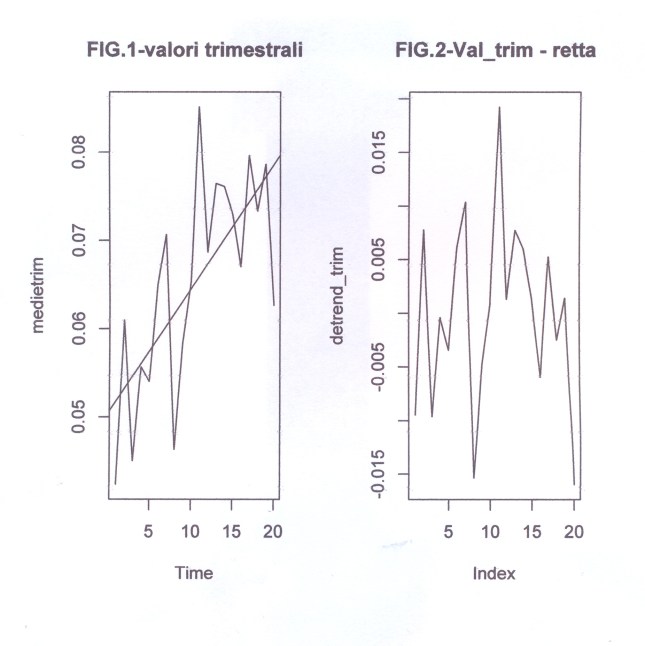
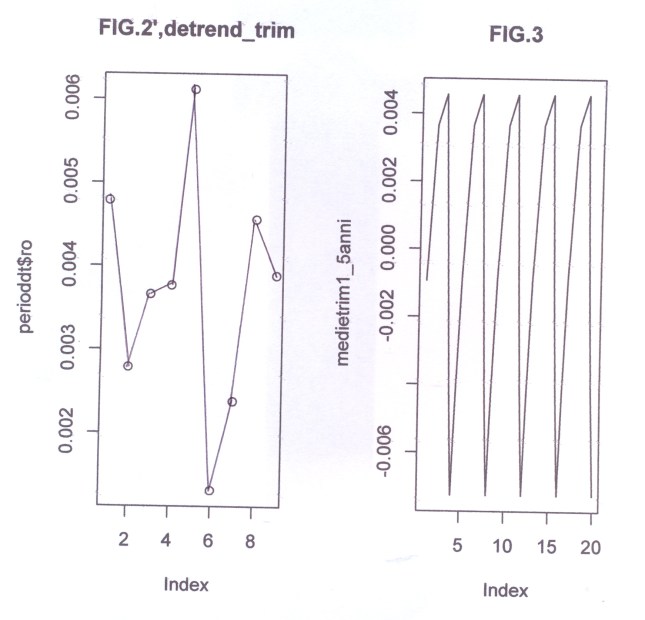
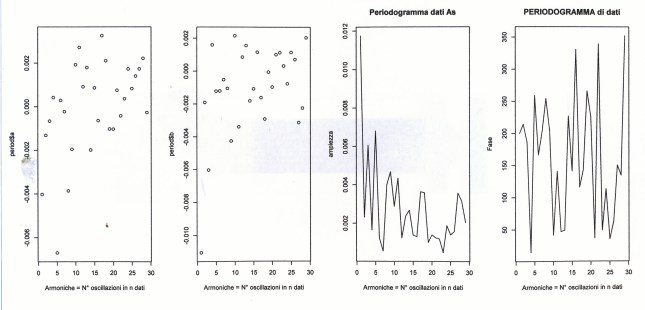
# PROVE_TEST SUL PERIODOGRAMMA E CONTROLLO COL MATHEMATICA 4.2 
# Oscillazioni su medietrim e costruzione delle formule 
trigonometriche
# Eliminazione delle varie armoniche

par(ask=T)
par(mfrow=c(1,3))
#medietrim sono i 20 valori trimestrali relativi ai 60 dati mensili delle concentrazioni arsenico 
#della Carlina per 5 anni, in studio.
#Vedere il Post a nome di P.Pistoia  "Un percorso verso il periodogramma" 
#in questo blog o rivisitato ed esteso in APPENDIX4.

yt=c(0.04233333,0.06100000,0.04500000,0.0556666,0.05400000,
0.06500000,0.07066667,0.04633333,0.05833333,0.06533333,
0.08516667,0.06866667,0.07650000,0.0761666,0.07300000,
0.06700000,0.07966667,0.07333333,
0.07866667,0.06266667)

#ALTRA PROVA IN COSTRUZIONE
#yt= qui si introduce il vettore detrend_trim, cioè i 20 valori di yt detrendizzato, 
#su cui faremo agire la function del periodogramma. Vedere  
APPENDIX4
# detrend_trim=c(-0.0094714286, 0.0077825815, -0.0096300752, 
#-0.0003760652, -0.0034553885, 
# 0.0061319549, 0.0103859649, -0.0153600251, -0.0047726817, 
0.0008146617, 
# 0.0192353383, 0.0013226817, 0.0077433584, 0.0059973684, 
0.0014180451, 
#-0.0059946115, 0.0052593985, -0.0024865915, 0.0014340852, 
-0.0159785714)
 
n=length(yt)
yt=as.vector(yt)
nx=n
yx=yt 
medietrim=yt




#m =(n-1)/2 # perché n dispari
#m =(n/2-1) # perché n pari

if (nx/2%%2==2) mx=nx/2-1 else mx=(nx-1)/2 #controllo 
automatico di n (pari o dispari?)
#Controllare se ho invertito le due opzioni!

nx
mx
t=c(1:length(medietrim))
PRDGRAM<- function(y1,n1,m1) {

# VALORI DEL PARAMETRO ak
a0=c(); k=0; a0=0;
for(t in 1:n1){a0=a0+y1[t]*cos(2*pi*t*k/n1)}
a0

a0=a0*2/n1;a0=a0/2

a0

a=c();a[1:m1]=0;
for(k in 1:m1) {
for(t in 1:n1){
a[k]=a[k]+y1[t]*cos(2*pi*t*k/n1)}}
a=2*a/n1

# vALORI DEL PARAMETRO bk

b=c();b[1:m1]=0;b0=0;k=0
for(k in 1:m1) {
for(t in 1:n1){
b[k]=b[k]+y1[t]*sin(2*pi*t*k/n1)}}

a <- as.vector(a)

for(i in 1:m1){
if (abs(a[i]) < 1e-10) a[i]=0 else a[i]=a[i]}
a

for(i in 1:m1){
if (abs(b[i]) < 1e-10) b[i]=0 else b[i]=b[i]}
b=2*b/n1
b
# AMPIEZZE
#ro[1:m1]=0
ro <- sqrt(a^2 +b^2)

for(i in 1:m1){
if (abs(ro[i]) < 1e-10) ro[i]=0 else ro[i]=ro[i]}

# CALCOLO DELLA FASE DI OGNI ARMONICA
# RIPORTANDO IL VALORE AL QUADRANTE GIUSTO
f2=c()
f2[1:m1]=0
for(i in 1:m1){
f2[i] <- abs(a[i]/b[i])
f2[i] <- atan(f2[i])*180/pi}
f2 =as.vector(f2)
f2
#f2[1:m1]=0 un f2[1:m1] di troppo!
phi <- c()
for(i in 1:m1){
# f2 <- abs(a[i]/b[i]);
# f2 <- atan(f2)*180/pi;
if(b[i]>0 & a[i]>0) phi[i] = f2[i];
if(b[i]<0 & a[i]>0) phi[i] = 180-f2[i];
if(b[i]<0 & a[i]<0) phi[i] = 180+f2[i];
if(b[i]>0 & a[i]<0) phi[i] = 360-f2[i];
if(b[i]==0 & a[i]==0) phi[i] = 0;
if((b[i]<0 & b[i]>0) | a[i]==0) phi[i]=0; 
if(b[i]==0 & a[i]>0) phi[i]=90;
if(b[i]==0 & a[i]<0) phi[i]=360-90
}

# PHI FASE ARMONICHE

phi=as.vector(phi)
phi
param_a <-a
param_b <-b
ampiezza <- ro
fase <- phi

a;b;ro;phi
# Qui, al termine della function si pone il valore di un'unica 
# variabile che esce o, se escono più variabili, si usa  
# un data.frame: data=data.frame(x1,x2,...).
# Ogni chiamata alla function permette di includere l'unica 
# variabile o i data nel nome della chiamata:
# es. periodxx=nome.function(x1,x2,...)

data <-data.frame(a,b,ro, phi) 
data
# questa matrice esce dalla function e viene 'raccolta' nella variabile periodxx

}

#FINE SUBROUTINE ANALISI FOURIER

period=PRDGRAM(medietrim,nx,mx)
period 
plot(period$ro,type="l",main="PERIODG.medietrim",
xlab="Armoniche = N° oscillazioni in n dati", ylab="ampiezza")
# 1° grafico in A1
# medietrim (vedere ro del  period. di medietrim) presenta 
# le armoniche rilev. n.3 e n.5 (GRAF.A1)

# for(i in 1:10000000) i=i
#data <-data.frame(param_a,param_b,ampiezza, fase)
#data
# Con il numero delle armoniche considerate rilevanti, 
le relative ampiezze e fasi possiamo
# costruire le loro espressioni trigonometriche.

w1=c(1:length(medietrim))
y_osc=0.0058*sin(2*pi*5*t/20+3.9) # questa oscillazione 
dovrebbe avere  
# un'armonica 5 (GRAF.A3)
so=medietrim-y_osc # so nel grafico dell'ampiezza (GRAF.B2). 
# Questa sottrazione eliminerà l'armonica 5
#  da ro di medietrim (GRAF.B2)

so
#PER UN'ALTRA PROVA

# Se consideriamo l'altra espressione y_osc1=0.0066*sin(2*pi*3*t/20+2.92), che ha un picco 
#all'armonica 3, invece di y_osc, e la sottraiamo da medietrim che ha pure un picco  
#all'armonica 3 (GRAF.A1), come diverrà il grafico? (vedere 
GRAF.B3)

#Se detrendiziamo medietrim (detrend_trim) e applichiamo il 
period. 
#potremo controllare le sue armoniche rilevanti e esprimere in forma analitica 
#(in formula trigonometrica) la loro rilevanza (y_oscxx). 
APPENDIX4 

#detrend_trim=c(-0.0094714286, 0.0077825815, -0.0096300752, 
#-0.0003760652, -0.0034553885, 
#0.0061319549, 0.0103859649, -0.0153600251, -0.0047726817, 
0.0008146617, 
#0.0192353383, 0.0013226817, 0.0077433584, 0.0059973684 
0.0014180451, 
#-0.0059946115, 0.0052593985, -0.0024865915, 0.0014340852, 
-0.0159785714) #ripreso dall'APPENDIX4
 
FINE ALTRA PROVA
ny=length(y_osc) 
n=length(so) 

if (n/2== n%%2) m=n/2-1 else m=(n-1)/2 
period1=PRDGRAM(so,n,m) 
period1 
period1$ro 
#plot(period1$ro,type="l",main="PERIODG.senza osc.5", 
#xlab="Armoniche = N° oscillazioni in n dati", ylab="ampiezza")

y_osc1=0.0066*sin(2*pi*3*t/20+2.92)# armonica 3; FIG.A2 
nz=length(y_osc1)

if (nz/2== nz%%2) mz=nz/2-1 else mz=(nz-1)/2

period6=c() 
period6=PRDGRAM(y_osc1,nz,mz) 
period6 
plot(period6$ro,type="l",main="PERIODG.y_osc1",
xlab="Armoniche = N° oscillazioni in n dati", ylab="ampiezza")# 2° grafico in A2

if (ny/2== ny%%2) my=ny/2-1 else my=(ny-1)/2 
period2=PRDGRAM(y_osc,ny,my)  
period2  
period2$ro  
plot(period2$ro,type="l",main="PERIODG.y_osc", 
xlab="Armoniche = N° oscillazioni in n dati", ylab="ampiezza") # 3° grafico in A3
 
period3=c() 
period3=period 
plot(period3$ro,type="l",main="PERIOD.medietrim", 
xlab="Armoniche = N° oscillazioni in n dati", ylab="ampiezza")
# 4° grafico in B1 
# medietrim (vedere ro del period. di medietrim)

 

so1=medietrim-y_osc1 
#period4=c() 
#period4=period1 
#plot(period4$ro,type="l",main="PERIODG.senza osc.3", 
#xlab="Armoniche = N° oscillazioni in n dati", ylab="ampiezza")

nz=length(y_osc1) 
if (nz/2%%2==2) mz=nz/2-1 else mz=(nz-1)/2 #controllo automatico di n (pari o dispari?) 
period5=c() 
period5=PRDGRAM(so1,nz,mz) 
period5 
plot(period5$ro,type="l",main="PERIODG.senza osc.3",  
xlab="Armoniche = N° oscillazioni in n dati", ylab="ampiezza") # 5° grafico in B3 
#par=(mfrow=c(1,1)) 
#period6=c() 
period6=PRDGRAM(y_osc1,nz,mz) 
#period6 
#plot(period6$ro,type="l",main="PERIODG.y_osc1",  
#xlab="Armoniche = N° oscillazioni in n dati", ylab="ampiezza")#

plot(period1$ro,type="l",main="PERIODG.senza osc.5", 
xlab="Armoniche = N° oscillazioni in n dati", ylab="ampiezza")
#6° grafico in B2

#RISULTATI OK

cliccare qui sotto per vedere i risultati degli scripts in pdf che verranno costruiti facendo girare il programma precedente.
period_prove_test (1)

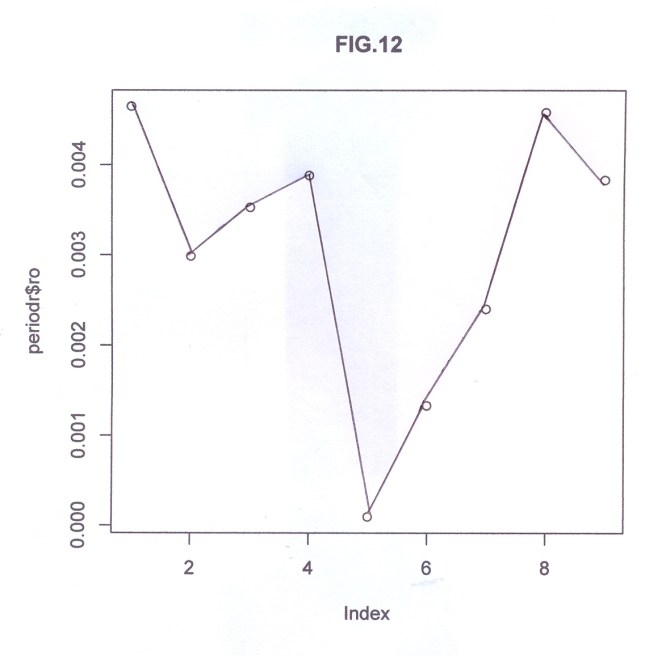
Si aggiungono qui i relativi tre grafici FIG.A, FIG.B, FIG.C costruiti dal programma precedente, e la successiva FIG.D, che illustra, alla rinfusa, l’appunto relativo alla formulazione delle due armoniche costruite su ampiezze e fasi dei risultati.

FIG.D

DA QUI IN POI QUALCOSA ANCORA DA CONTROLLARE

PER VEDERE LA PRIMA VERSIONE DEL PRECEDENTE PROGRAMMA IN PDF 
CLICCARE SOTTO:

function_period_ok_3_richiami_result-p_pistoia-1 (1) 

LA NUOVA VERSIONE DEL PRECEDENTE PROGRAMMA CON IN USCITA 12 
GRAFICI SI TROVA CLICCANDO SU:
 
 function_period_ok_3_richiami_result-p_pistoia (1)

 
Una volta compreso come richiamare e come gestire i risultati 
della function del periodogramma, 
ora siamo in grado di continuare di volta in volta la 
correzione.

#In ogni caso gli scripts dei programmi presentati in R possono essere trasferiti, anche 
#un pezzo alla volta, direttamente sulla console di R con Copia-Incolla: il programma inizierà 
#nell'immediato a girare costruendo risultati e grafici i cui 
significati sono riassunti 
#nei remarks.

Ho scritto le precedenti routines che sembrano funzionare, come si vede dai risultati, considerando il periodogramma come una function, una specie di subroutine. Sarò costretto comunque a rimettere in discussione con calma altri programmi in R che contengono questa function tenendo conto dei cambiamenti!

CHI VOLESSE PUO’ VEDERE ANCHE GLI SCRIPTS DELLO STESSO AUTORE RELATIVI AL PERIODOGRAMMA E ALL’ANALISI DI FOURIER IN MATHEMATICA DI WOLFRAM VERS. 4.2, per fare un controllo dei risultati. Sono inseriti nelle appendici.

IL CONTROLLO DEI PROGRAMMI IN R CHE SEGUONO E’ QUASI COMPLETATO

AD MAIORA

CHIUSA PARENTESI

________________________

6_CENNO A COMANDI IN R DI CALCOLO E ORGANIZZAZIONE DEI DATI

Filter, matrix e ts di R.
Discussione sui comandi di calcolo ed organizzazione sui dati. Commento sulle prime istruzioni di R (file di dati). Processi per automatizzare i “i conti”.

Si usa la funzione ts di R che riorganizza direttamente la serie originale (yt o as1)
in 12 colonne (mesi) e 5 righe (anni) per il calcolo poi con un for delle medie di tutti i Gennaio, di Febbraio…

Discussione su filter

Applico direttamente la funzione Filter di R, sempre sulla serie originale (yt o as1), che, eliminando da essa (cioè da as1) la componente stagionale di ordine 12 + random, cambia contenuto in TREND + Ciclo + random? (divenendo la asf12). Trovo poi la retta di regressione su asf12, i cui valori delle sue ordinate verranno tolti dalla serie originale; faccio il grafico di asf12 + retta di regr . Da controllare meglio. Smussando la yt, la asf12 è senza random? Vedere dopo gli script.

SEGUE IL COMMENTO SULLE LE PRIME ISTRUZIONI DI R PER AUTOMATIZZARE I ‘CONTI’ DEL PROCESSO RIASSUNTO IN PRECEDENZA CHE ESPANDEREMO IN UN SECONDO TEMPO

I PRIMI INTERVENTI IN R

I primi passi nella schermata iniziale di R consistono nel caricare le Librerie suppletive di R necessarie a fornire i comandi, oltre a quelli di base, per gestire ed elaborare i dati sperimentali. Con la funzione getwd() capisco dove ‘guarda’ R (cioè qual è la directory di lavoro) per cercare il file-dati da caricare e la funzione setwd (directory) permette di cambiare tale directory di lavoro. Fatta conoscere ad R la directory di lavoro, gli facciamo leggere il file-dati scelto per l’analisi (con il comando read.csv); nella fattispecie “As-Carlina1.csv”; la funzione file.show(“nome file.csv”) permette di visionare il contenuto del file che in generale è una matrice con righe e colonne è cioè un data.frame a cui si attribuisce un nome (per es., frame) e di cui è possibile conoscere le dimensioni col comando dim() o estrarre elementi. Le righe della matrice sono le osservazioni o casi; le colonne sono i campi o variabili. Con frame$variable si vuol dire di estrarre la variabile chiamata variable dal data.frame chiamato frame; frame[1,] significa prendere la prima riga, mentre frame[,3], prendere la terza colonna e così via. L’espressione summary(frame$variable) trova tutti i valori della variabile variabile contenuti nel data.frame chiamato frame. Così summary(frame[,3]), trova tutti i valori della colonna 3.

library (stats)

library(tseries)

library(lattice)

#library(graphics)

#getwd()

#setwd(“E:/R-2.12.2/bin/i386”)

# Se conosco dove è memorizzato il file con i dati da analizzare e la sua struttura

# utilizzo questi scripts iniziali

#as=read.csv(“As-Carlina.csv”)

#as1=as[,5]

#leggo la quinta colonna del data.frame: As-Carlina.csv dove c’è appunto yt

#as1=ts(as1) # considero as1 una serie storica

#ts.plot(as1) # plotto as1

Introdurremo invece direttamente la Serie yt o as1

as1= c(.033,.043,.051,.059,.061,.063,.053,.036,.046,.056,.063,.048,.053,.043,

.066,.053,.082,.06,.08,.076,.056,.036,.05,.053,.056,.058,

.061,.063,.065,.068,.0815,.095,.079,.063,.069,.074,.08,.0765,.073,

.0695,.066,.093,.083,.073,.063,.074,.067,.06,.086,.08,.073,.067,

.089,.064,.087,.079,.07,.065,.06,.063)

7 – ECCO QUELLO CHE FAREMO CON R: ‘LETTURE’ SUI PROCESSI (‘CACCIA AI RESIDUI’ compresa)

ECCO QUELLO CHE FAREMO CON R

RIORGANIZZAZIONE DELLA SERIE STORICA MENSILE LUNGA CINQUE ANNI, As1, IN DODICI COLONNE (mesi) E CINQUE RIGHE (anni) E BREVI LETTURE SUCCESSIVE

Il primo passo è riorganizzare la serie storica mensile della durata di 5 anni (5×12=60 mesi), in 12 colonne (mesi) e 5 righe (anni).

In ogni colonna ci sono 5 valori di ogni mese: nella prima, i 5 valori di gennaio, nella seconda, i 5 di febbraio e così via, Questo insieme costituisce il file as1.ts1. Per costruire as1.ts1 si può con R operare in almeno due modi. Una volta costituita la classificazione as1.ts1, si usa la funzione ts che permette poi tramite la subas, di meccanizzare con un for il calcolo delle dodici medie riferite ad ogni mese per i 5 anni (vedere dopo).

In sintesi con ts, che ha come argomenti: file, start e frequency, raggruppo i dati con i valori di ogni mese nella stessa colonna. Nella tabella appaiono il nome dei mesi su ogni colonna e il nome degli anni ad ogni riga; siamo così in grado di prendere i cinque dati di ogni mese (uno ogni dodici) per farne la media.

as1.ts1=ts(as1,start=1989,frequency=12)

Questa espressione fa anche la media di ogni colonna?

subas=as1.ts1[seq(1, length(as1), by=12)]

subas raccoglie i dati di gennaio per i 5 anni e ne fa la media(0.064); per ulteriori elaborazioni si può automatizzare con for.

Con for ottengo le 12 medie di ogni mese per 5 anni, mettendo un i al posto di 1 nell’argomento.

Guardiamo come.

mediamesi=c()

for(i in 1:12){mediamesi[i]=mean(as1.ts1[seq(i,length(as1),by=12)])}

ts.plot(mediamesi)

Se togliamo dal vettore mediamesi la media di as1, si ottiene una sorta di Effetto Stagionale mensile.

Mediamesi0=c()

Mediamesi0 =(mediamesi – mean(as1)) # da errore!

ts.plot(mediamesi0) # da errore! In effetti (vedere gli scripts al termine), non so perchè, sono necessarie variabili intermedie.

Vedremo dopo altri modi per il calcolo dell’Effetto Stagionale attraverso una Media Mobile e la funzione filter su as1, ambedue di ordine 12, modificando la stessa as1 o yt, in Mbt e asf12 di 12 termini più corte rispettivamente, contenenti ambedue almeno TREND lin.+ Ciclo (il random plausibilmente si cancellerebbe nel processo). La serie originale era pensata costituita da componente stagionale + TREND_ lin. + ciclo + random.

Calcolo la Media Mobile di ordine 12 su yt o as1; trovo la serie Mbt di 12 termini più corta, che è yt smussata della stagionalità, che serve a calcolare l’Effetto Stagionale, passando attraverso la sottrazione yt – Mbt , chiamata STRD (stagionalità più random: Tabella 1, colonna 7, APPENDIX 3).

yt=as.vector(yt): n=length(yt); Mbt=c()

for(t in 7:n){Mbt[t] = (yt[t-6]/2+yt[t-5]+yt[t-4]+yt[t-3]+yt[t-2]+yt[t-1]+yt[t]+yt[t+1]+yt[t+2]+yt[t+3]+yt[t+4]+yt[t+5]+(yt[t+6])/2)/12}

Mbt # di 12 termini più corta: 6 NA all’inizio e 6 NA alla fine, in tutto 48 dati (yt o as1 erano 60)

Mbt=Mbt[7:54]# elimino da Mbt gli NA; se i dati iniziali iniziavano da gennaio, Mbt inizia da un luglio e termina a un giugno

In alternativa applico il filter di ordine 12 su as1 o yt:

asf12=filter(yt, filter=rep(1/13,13)) # 12 o 13?

asf12

asf12=asf12[7:54] # elimino da asf12 gli NA

Le deboli differenze fra Mbt e asf12 è facile siano dovute alla Media Mobile manuale che è centrata.

Scorcio la as1 di 6 valori iniziali e finali per renderla lunga come Mbt e poi vi sottraggo Mbt:

STRD=as1[7:54] – Mbt # il primo valore di STRD corrisponde a luglio del primo anno.

Ciò significa: STRD= (ciclo+TREND+stagionalità+random) – (ciclo+TREND)=stagionalità+random; 60-12=48 termini.

Si calcola ora il Fattore Stagionale mensile (Tabella 1, colonna 8; 12 termini, APPENDIX 3) agendo con la funzione matrix su STRD e successivamente con colMeans: metto STRD (48 termini) sotto forma di matrice con dodici colonne (mesi) e 4 righe (anni)

stag = matrix(STRD, ncol=12, byrow=T)

Su questa matrice col comando colMeans posso trovare le 12 medie dei 4 valori, una per ogni mese, che metto in mediacol:

mediacol = colMeans(stag) # in mediacol rimangono i random?

Ordino le 12 medie ottenute, che iniziano da luglio del primo anno e terminano a giugno dell’anno successivo, da gennaio a dicembre:

mediacol=(mediacol[7:12],mediacol[1:6]) # Controllare se funziona!

mediacol # detto talora Fattore Stagionale

Copro poi i 5 anni ripetendo questi 12 valori:

ESAs = rep(mediacol,5) # Effetto stagionale di yt o as1

ESAs # serie lunga come yt o as1 originale

Dobbiamo ora togliere da yt o as1 l’Effetto Stagionale trovato per ottenere la serie iniziale destagionalizzata (stg, detta anche y1t o dst; Tabella 2, colonna 2) :

stg=c() #forse è meglio chiamala dst o y1t al posto di stg

dst=c() # dst o y1t in stg!

dst= yt–ESAs # TREND+ciclo_random; serie originale destagionalizzata (GRAF. N.4 a- CORR; b-PERIOD))

# Di fatto questa istruzione stranamente dava errore; forse è necessario introdurre variabili intermedie (vedere scripts relativi dopo). Controllare meglio!

# dst <- c(as1–ESAs) # TREND+ciclo_random #ancora da rifletterci!

dst # è la serie originale destagionalizzata (in altre occasioni chiamata y1t). Di questa disegno il correlogramma: i dati sono autocorrelati; la statistica DW , per K= 1, N=60, rischio 0.05, cade a sinistra dell’intervallo dl-1.62 e si intravede la presenza di un TREND positivo (GRAF. N.4 a); dal periodogramma è sparito completamente il picco di frequenza 5 (periodo 60/5) dell’oscillazione stagionale (GRAF. N.4 b), presente invece nel periodogramma della serie originale (GRAF. N.2 b) e nell’ESAs (GRAF. N.3 b).

y1t=dst

6-7 LA ‘CACCIA’ AI RESIDUI

Potremmo tentare di togliere da dst o y1t (TREND+ciclo_random) i random, provando a perequare con una Media Mobile 3*3 (pesata 1,2,3,2,1) per cui l’yt_smussato verrebbe a contenere ciclo+TREND che, tolto da dst o y1t, dovrei ottenere i random, se le ipotesi iniziali fossero giuste (vedere il testo di questi scripts già in Blocco Note con i risultati relativi, nel paragrafo prima delle Appendici (SECONDA PARTE). Alcuni ricercatori infatti propongono medie mobili a tre o 5 termini pesati 12321, per eliminare i random! PROVIAMO invece il tentativo più classico che Segue: detrendizziamo linearmente la dst o y1t, sottoponendola ad una regressione lineare semplice (RLS)…

8 – INIZIO COPIA SCRIPTS DEL PROGRAMMA CENTRALE
Vari commenti possibili e riflessioni alternative

INIZIANO GLI SCRIPTS DEL PROGRAMMA RELATIVO A TUTTO IL PROCESSO DESCRITTO E DISCUSSO IN PRECEDENZA

Da copiare sul Blocco Note con copia/incolla e poi sulla consolle di R (o direttamente su R). In generale i programmi scritti in R o si fanno girare scrivendo una istruzione dietro l’altra , oppure, per es., si copiano gli scripts sul Blocco Note od altro semplice programma di scrittura (anche quelli indirizzati ad R), con copia/incolla e poi sulla consolle di R.

Altro problema in R, quando si copiano programmi pronti dal Blocco Note, è quello di gestire la visione dei diversi grafici, man mano che il programma gira. In questo caso è necessario che il programma controlli i grafici nel senso, per es., di far fermare il programma all’apparire del grafico nella finestra grafica, nella attesa della pressione di un tasto. Per questo esiste un semplice comando, da inserire, per es., all’inizio degli scripts, che ha la sintassi: par(ask=T). Si può utilizzare in alternativa o insieme il comando par(mfrow=c(x,y) , che divide l’unica finestra grafica in x*y parti; x=2 e y=3, la finestra rimane divisa in 6 parti e può contenere 6 grafici e così via.

COMMENTO

Il seguente programma è stato utilizzato da prima nell’analisi della serie As originale, nel modo come era nato, cioè iniziando il lavoro con l’applicare la media mobile direttamente sulla serie originale, arrivando però ad una serie residuale che può non rispettare i criteri richiesti (rivedremo i passaggi). Questo primo modo è quello che per ora continua a venire presentato e commentato.

Per osservare il percorso che parte invece, forse più giustamente, dalla serie detrendizzata (il trend in una serie può ‘disturbare’ il computo dell’Effetto Stagionale?), basta sostituire nel vettore as1, invece dei valori originali, i valori della serie detrendizzata, nel nostro caso per es. copiati dai programmi del Mathematica di Wolfram (Appendix 5) o dall’altro post ‘Verso il periodogramma’, sempre dello stesso autore o… si rifaccia il conto. Basta togliere il cancelletto (#) all’as1 che riporta i valori della serie detrendizzata e ‘cancellettando’ invece i valori dell’as1 che riporta quelli della serie originale (e viceversa). I risultati ipoteticamente dovrebbero migliorare. Proviamo.

RESIDUI ANALISI SU As1 DETRENDIZZATO-P_Pistoia

Col tempo e la pazienza è possibile che riporti, in un link, il programma in pdf che, in as1, ha i suoi valori detrendizzati, con più di una decina di grafici relativi, con risultati e commenti! Vedere sopra la prima versione.

8-INIZIO COPIA PROGRAMMA

library(tseries)

library(lattice)

library(graphics)

as1= c(.033,.043,.051,.059,.061,.063,.053,.036,.046,.056,.063,.048,.053,.043,.066,.053,

.082,.06,.08,.076,.056,.036,.05,.053,.056,.058,

.061,.063,.065,.068,.0815,.095,.079,.063,.069,.074,.08,.0765,.073,

.0695,.066,.093,.083,.073,.063,.074,.067,.06,.086,.08,.073,.067,

.089,.064,.087,.079,.07,.065,.06,.063)

# Per partire con la detrendizzazione, ad as1 sostituiamo i valori della stessa serie detrendizzata.

# Togliamo il cancelletto e mettiamo la nuova serie detrendizzata qui e ‘cancellettiamo’ la precedente:

#as1 =c(-.018,.0089,-.0013,.0062,.0077,.0093,

#-.0012,-0.0187,-.0091,.00039,.0069,-.0085,

#-.0040,-.014,.0080,-.0054,.0231,.00064,

#.0202,.0157,-.0048,-.0252,-.0117,-.0092,

#-.0066,-.0051,-.0026,-.0011,.00048,.0030,

#.0160,.029,.013,-.0039,.0017,-.0092,

#.012,.0076,.0038,-.00018,-.0042,.0223,

#.012,.0014,-.0090,.0015,-.0060,-.0134,

#.0121,.0056,-.0018,-.0083,.0132,-.00122,

#.0102,.0018,-.0077,-.0131,-.0186,-.0161)

as1=ts(as1)

par(ask=T)

par(mfrow=c(1,2))

yt=c()

yt=as1

ts.plot(yt, main=”GRAF. N.2_yt_ SERIE CORRETTA”)

lines(yt,type=”l”)

acf(yt, main=”GRAF. N.2_a-yt_CORR_SERIE CORRETTA”)

#alfa=-pi/2 -> 270°; alfa=-1.175 rad (cioè -100°) -> 260°

#INIZIO FUNCTION

PRDGRAM<- function(y1,n1,m1) {

# VALORI DEL PARAMETRO ak

a0=c(); k=0; a0=0;

for(t in 1:n1){a0=a0+y1[t]*cos(2*pi*t*k/n1)}

a0=a0*2/n1;a0=a0/2

a=c();a[1:m1]=0;

for(k in 1:m1) {

for(t in 1:n1){

a[k]=a[k]+y1[t]*cos(2*pi*t*k/n1)}}

a=2*a/n1

# vALORI DEL PARAMETRO bk

b=c();b[1:m1]=0;b0=0;k=0

for(k in 1:m1) {

for(t in 1:n1){

b[k]=b[k]+y1[t]*sin(2*pi*t*k/n1)}}

a <- as.vector(a)

for(i in 1:m1){

if (abs(a[i]) < 1e-10) a[i]=0 else a[i]=a[i]}

for(i in 1:m1){

if (abs(b[i]) < 1e-10) b[i]=0 else b[i]=b[i]}

b=2*b/n1

# AMPIEZZE

#ro[1:m1]=0

ro <- sqrt(a^2 +b^2)

for(i in 1:m1){

if (abs(ro[i]) < 1e-10) ro[i]=0 else ro[i]=ro[i]}

# CALCOLO DELLA FASE DI OGNI ARMONICA

# RIPORTANDO IL VALORE AL QUADRANTE GIUSTO

f2=c()

f2[1:m1]=0

for(i in 1:m1){

f2[i] <- abs(a[i]/b[i])

f2[i] <- atan(f2[i])*180/pi}

f2 =as.vector(f2)

#f2[1:m1]=0 un f2[1:m1] di troppo!

phi <- c()

for(i in 1:m1){

# f2 <- abs(a[i]/b[i]);

# f2 <- atan(f2)*180/pi;

if(b[i]>0 & a[i]>0) phi[i] = f2[i];

if(b[i]<0 & a[i]>0) phi[i] = 180-f2[i];

if(b[i]<0 & a[i]<0) phi[i] = 180+f2[i];

if(b[i]>0 & a[i]<0) phi[i] = 360-f2[i];

if(b[i]==0 & a[i]==0) phi[i] = 0;

if((b[i]<0 & b[i]>0) | a[i]==0) phi[i]=0;

if(b[i]==0 & a[i]>0) phi[i]=90;

if(b[i]==0 & a[i]<0) phi[i]=360-90

}

# PHI FASE ARMONICHE

phi=as.vector(phi)

phi

param_a <-a

param_b <-b

ampiezza <- ro

fase <- phi

# Qui, al termine della function si pone il valore di un’unica

# variabile che esce o, se escono più variabili, si usa

# un data.frame: data=data.frame(x1,x2,…).

# Ogni chiamata alla function permette di includere l’unica

# variabile o i data nel nome della chiamata:

# es. periodxx=nome.function(x1,x2,…)

data <-data.frame(a,b,ro, phi)

data

# questa matrice esce dalla function e viene ‘raccolta’ nella variabile nomexx (es.,periodxx)

}

#FINE FUNCTION

#Per richiamare la function:

#nomexx = PRDGRAM(Nome_var_vettore dati, numerosità del campione, numero di armoniche da cercare)

yt=as1

yx=as1

nx=length(yt)

#periodogramma yt

if (nx/2== nx%%2) mx=nx/2-1 else mx=(nx-1)/2 #da controllare se non sia necessario uno swap!

period_as1= PRDGRAM(yx, nx ,mx)

#par(mfrow=c(1,4)) 
#plot(a, xlab="Armoniche = N° osc. in n dati") 
#plot(b, xlab="Armoniche = N° osc. in n dati")

 period_as1 # tabella dei dati in uscita: ak, bk, ampiezze, fasi
# Con questa tabella si costruiscono le formule analitiche delle armoniche

period_as1$ro # vettore delle ampiezze

plot(period_as1$ro,type="l",main="GRAF. N.2; a-period_yt", 
xlab="Armoniche = N° oscill. in n dati", ylab="ampiezza")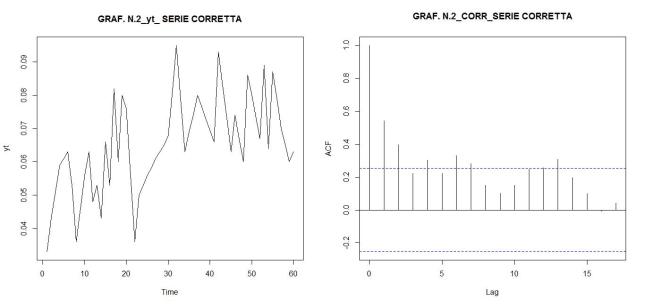

par(mfrow=c(1,4))

plot(period_as1$a,ylab="Parametro a")
plot(period_as1$b,ylab="Parametro b") 
plot(period_as1$ro,type="l",main="PERIODOGRAMMA di as1", 
xlab="Armoniche = N° osc. in nx dati", ylab="ampiezza") 
plot(period_as1$phi,type="l", ylab="Fase")

#Per vedere i risultati trasferiti dalla consolle di R in pdf
#del precedente frammento di programma cliccare sotto:
As1_corr_R - P. Pistoia

par(mfrow=c(1,1)) 

as1.ts1=ts(as1,start=1989,frequency=12)
subas=as1.ts1[seq(1,length(as1),by=12)]

#-----------------------------------------------

# Gli scripts che riguardano il calcolo delle variabili vettoriali mediamesi e Mmesio per ora sono esclusi.

#mediamesi=c()

#for(i in 1:12){mediamesi[i]=mean(as1.ts1[seq(i,length(as1),by=12)])}

#ts.plot(mediamesi,main”mediamesi in 5 anni”)

#Mmesi0=c()

#a=mediamesi

#b=mean(as1)

#c=a-b

#Mmesi0=c () 12 valori medi meno la media serie originale; una specie di Effetto Stagionale

#Mmesi0=mediamesi – mean(as1)

#ts.plot(Mmesi0) # da controllare: Effetto Stagionale da confrontare con mediacol

#acf(Mmesi0, main=”CORR_Mmesi0″)

#Mmesi0 # da confrontare con mediacol

#—————————————————————————–

yt=as1

yt=as.vector(yt); n=length(yt); Mbt=c()

for(t in 7:n){Mbt[t] = (yt[t-6]/2+yt[t-5]+yt[t-4]+yt[t-3]+yt[t-2]+

yt[t-1]+yt[t]+yt[t+1]+yt[t+2]+yt[t+3]+yt[t+4]+yt[t+5]+(yt[t+6])/2)/12}

#SI LAVORA ORA SU Mbt

Mbt #è quello che resta di as1, dopo la media mobile 12 (trend-ciclo_random)

Mbt=Mbt[7:54]# elimino da Mbt gli NA; Tabella N.1, colonna 6.

ts.plot(Mbt, main=”GRAF. N.4′; Mbt )

acf(Mbt, main=”GRAF. N.4′; acf_Mbt”)

#Periodogramma Mbt, serie più corta senza stagionalità

y3=c()

y3=Mbt

n3==length(y3)

if (n3/2== n3%%2) m3=n3/2-1 else m3=(n3-1)/2

#ifelse(nx%%2 > 0, m=(n-1)/2, m=n/2-1

period_Mbt=PRDGRAM(y3, n3 ,m3)

period_Mbt # tabella ak, bk,ro,phi

period_Mbt$ro #valori ampiezza di Mbt

ts.plot(period_Mbt$ro, main=”GRAF. N.4′; period_Mbt”)

# Filtro col comando filter la serie yt

asf12=filter(yt, filter=rep(1/13,13))

asf12

asf12=asf12[7:54] # elimino da asf12 gli NA

#Mbt contiene l’as1 senza la stagionalità; in as1 però rimane quello

#che aveva ( trend-stagionalità-ciclo_random); se da as1, tolgo as1 senza la stagionalità,

#trovo la stagionalità e random (STRD) che trasformo in Effetto Stagionale eliminando

#una buona parte dei random.

FINE OPERAZIONI SU Mbt

#INIZIO CALCOLI CHE PORTANO ALL’EFFETTO STAGIONALE

STRD=as1[7:54]-Mbt # componente stagionale + random, serie più corta

STRD # da essa si estraggono gli Effetti Stagionali; TABELLA N.1, colonna 7:APPENDIX 3.

#Processo per costruire gli Effetti Stagionali attraverso STRD

stag = matrix(STRD, ncol=12, byrow=T) # variabile di passaggio a mediacol

mediacol = colMeans(stag) #in mediacol rimangono i random? o si perdono nella mediazione; 12 valori osc. annuale.

# in questo primo mediacol ottengo 12 valori a partire da luglio; TABELLA N.1, colonna 8; APPENDIX 3.

mediacol=c(mediacol[7:12], mediacol[1:6]) # qui ordino da gennaio a dicembre i 12

#valori dell’ EFFETTO STAGIONALE;

mediacol # è detto anche Fattore Stagionale; TABELLA N.1, colonna 8; APPENDIX 3.

#ts.plot(mediacol) # L’oscillazione annuale che copre 12 mesi (max in luglio)

ESAs = rep(mediacol,5) # l’Effetto Stagionale che ‘copre’ i 60 dati di yt o as1

ESAs #serie lunga come yt o as1 originale; TABELLA N.2, colonna 1; APPENDIX 3.

ts.plot(ESAs,main=”GRAF. N.3′; EFFETTO STAGIONALE”)

ESAs1 = rep(mediacol,2)

ts.plot(ESAs1,main=”GRAF. N.3; a-“EFFETTO STAGIONALE RLS”) #2 ascillazioni

acf(ESAs1, main=”GRAF. N.3′; b-CORR_EF. STAG. 2 ripet”)

#periodogramma ESAs1

yes=ESAs1

nes=length(ESAs1)

if (nes/2== nes%%2) mes=nes/2-1 else mes=(nes-1)/2

period_ESAs1=PRDGRAM(yes, nes, mes)

period_ESAs1

period_ESAs1$ro

plot(period_ESAs1$ro,type=”l”, main=”GRAF. N.3; b-Period_ro EFFETTO STAG.”)

dst=c() #attivo la serie destagionalizzata; dst o y1t ; TABELLA N.2, colonna 2; APPENDIX 3.

dst=as1-ESAs # da provare se funziona; destagionalizza

dst

#e=as1

#f=ESAs

#g=e-f

#dst=g

#Potrei smussare dst con una Media Mobile Pesata (3*3, cioè con pesi 1,2,3,2,1) per tentare

#di eliminare la componente casuale

#Si otterrebbe una serie (y1t) contenente CICLO+TREND, che se la tolgo dalla serie destagionalizzata

#dst precedente dovrei ottenere il #RESIDUO.

yd=dst

nd=length(dst)

if (nd/2== nd%%2) md=nd/2-1 else md=(nd-1)/2

period_dst=PRDGRAM(yd, nd, md)

period_dst

period_dst$ro

plot(period_dst$ro,type=”l”,main=”GRAF. N.4: b-Period. dst o y1t”)

#PROVIAMO INVECE A TOGLIERE IL TREND DALLA dst o y1t

plot(dst,type=”l”, main=”yt-destagionalizzata”) # la y1t o dst= yt destagionalizzata= ciclo+TREND +random (GRAF. N.4′)

acf(dst, main=”GRAF. N4; a-CORR-y1t o dst”)

# Se elimino il TREND da dst ottengo CLRD e posso controllare con CORR se

# ciò che resta è da considerare residuo. yt-ESAs-TREND = CLRD

# CLRD =yt-TREND- ESAs

#Calcolo il trend di dst per toglierlo da yt-ESAs o da y1t ed ottenere CLRD

t=seq(1:60)

fitdst=lm(dst~t)

abline(lm(dst~t))

summary(fitdst)

resid(fitdst)

p=predict(fitdst,data.frame(t=c(1,60)))

CLRD=c()

CLRD=dst-p

CLRD

CLRD=yt-ESAs-p

n1=length(p)

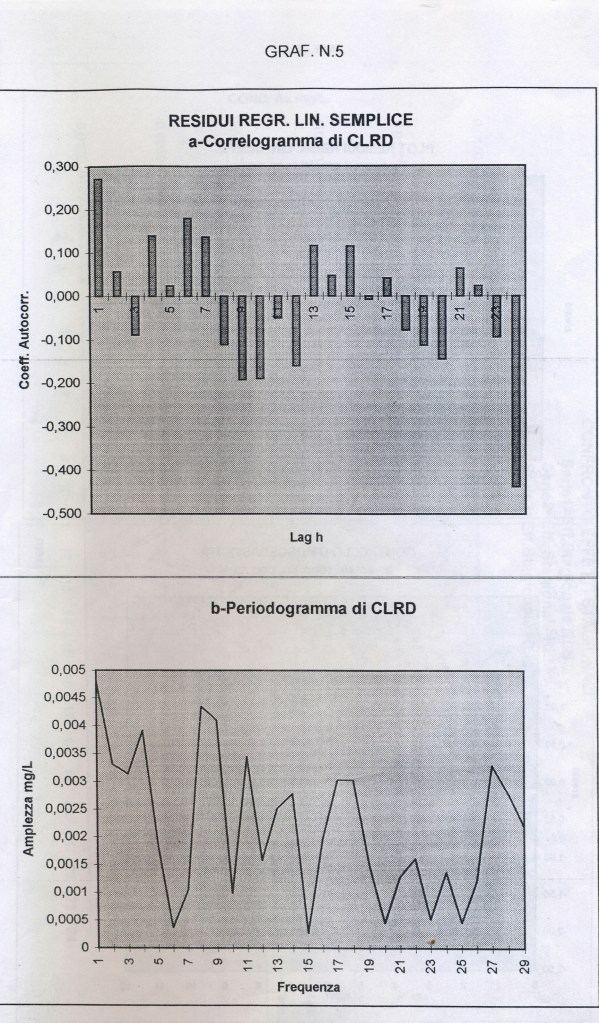
ts.plot(CLRD, main=”GRAF. N.5-RESIDUI” )

acf(CLRD, main=”GRAF. N.5; a-CORR_CLRD”)

#periodogramma di CLRD

yr=CLRD

nr=length(yr)

if (nr/2== nr%%2) mr=nr/2-1 else mr=(nr-1)/2

period_clrd=PRDGRAM(yr, nr ,mr)

period_clrd

period_clrd$ro

plot(period_clrd$ro,type=”l”,main=”GRAF. N.5; b-Period. CLRD”)

#da controllare ancora!

#FINE COPIA PROGRAMMA da trasferire in Blocco Note o direttamente sulla consolle di R

PER VEDERE SCRIPS E COMMENTI PRECEDENTI + RESULT IN pdf CLICCARE SOTTO:

ANALI SU As1 DETRENDIZZATO-P_Pistoia

BLOCCO_NOTE_PERCORSO_PERIOD0-P_Pistoia

BLOCCO_NOTE_PERCORSO_PERIOD-P_Pistoia

COMMENTO

Sembra che in questo processo CLRD (residui) non siano random e siano correlati (da provare altri tests). Proviamo però a fare altre misure di controllo. Se è così percorriamo altre vie già accennate. Possiamo partire col detrendizzare la serie originale as1, rendendola nelle previsioni stazionaria, e procedere con gli stessi scripts già usati.

Se ai dati originali di as1 sostituiamo i dati originali senza però il trend rettilineo (serie originale detrendizzata, nelle previsioni resa stazionaria), possiamo vedere che cosa accade. In effetti sembrerebbe che, se invece partiamo coll’applicare una media mobile di ordine 12 su una serie non stazionaria, si possa arrivare a questo risultato.

Se si parte con una detrendizzazione (serie stazionaria) e poi si applica la media mobile per trovare gli Effetti Stagionali, che togliamo dalla serie originale, e si procede con successiva detrendizzazione su serie_originale- Eff. Stag., si prevede un aumento dell’ R-quadro e forse un risultato più idoneo.

Si fa prima una regressione sulla serie di partenza; attraverso una media mobile si cercano gli Effetti Stagionali che togliamo dalla serie originale (la non stazionarità può disturbare gli effetti stagionali), ottenendo la serie originale destagionalizzata; si fa infine una seconda regressione su questa differenza, cioè sulla serie destagionalizzata, che può contenere appunto TREND + CICLO_RANDOM, ricavando poi il CICLO_RANDOM (da verificare).

Altro percorso: analisi dei dati trimestrali della stessa serie as1.

9 – PRIMA PARTE IN SINTESI

PRIMA PARTE IN SINTESI

LA SERIE PEREQUATA Mbt, L’EFFETTO STAGIONALE ESAs, LA SERIE DESTAGIONALIZZATA y1t (dst), LA y1t SMUSSATA: ciclo+TREND (y1ts),

LA COMPONENTE CASUALE O RESIDUI

IL CORRELOGRAMMA, IL TEST DI DURBIN WATSON e di LINMUDHOLKAR

Dopo aver eliminato la componente stagionale (ESAs : APPENDIX3, TABELLA N.2, col.1) dalla serie originale yt (APPENDIX3, TABELLA N.1, col.5) sottraendo yt – ESAs, si ottiene la serie destagionalizzata (dst ovvero y1t: APPENDIX3, TABELLA N.2, col.2). In questa serie sanno rimasti gli eventuali ciclo, TREND e la componente random. Sottopongo quest’ultima al programma CORR : i dati sono autocorrelati positivamente (la statistica di Durbin Watson , per k= 1, N=60 e rischio 0.05, cade a sinistra dell’intervallo dl-du (1.55-1.62) e si nota la presenza un TREND positivo (GRAF. N.4 a); dal periodogramma è completamente scomparso il picco di frequenza 5 (periodo 60/5) dell’oscillazione stagionale (GRAF. N.4 b), presente invece nel periodogramma della serie originale (GRAF. N.2 b) e nell’ESAs (GRAF. N.3 b). Leggere Appendice 1.

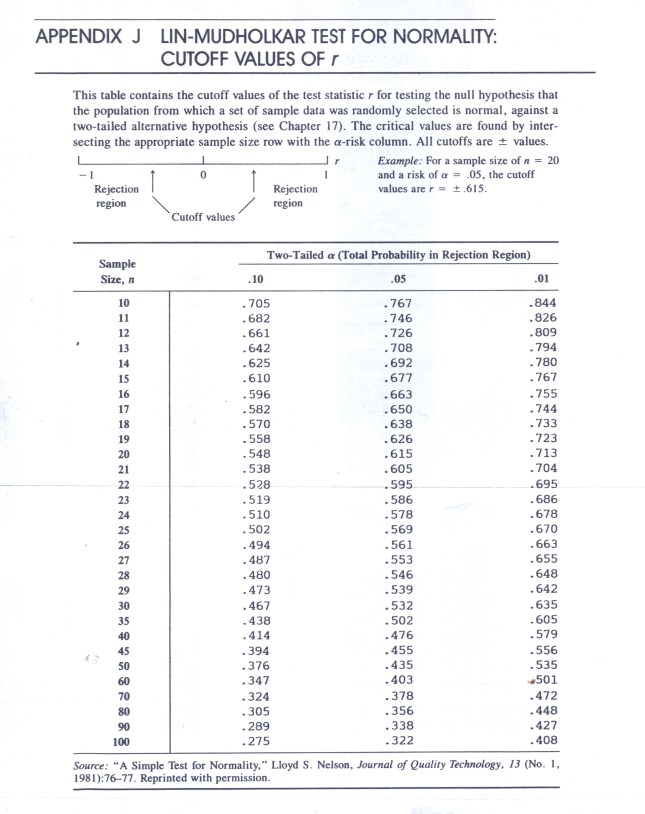
Smussiamo la serie y1t o dst con una media mobile pesata 3*3 (1,2,3,2,1), per eliminare la componente casuale. Si ottiene così la serie y1ts (CLTR : APPENDIX3, TABELLA N.2, col.3) che potrebbe contenere nelle previsioni ciclo e TREND (CLTR). Sottraendo da y1t o dst (ciclo+TREND+Random) la serie y1ts che potrebbe contenere ciclo+TREND si dovrebbe ottenere la componente casuale o serie random. Testando tale serie col programma CORR, risulta che essa è rumore di fondo (white noise), avvalorando il processo usato fino a questa fase. Infatti la DW, per k=1, n=60 e alfa =0.05, ha valore 2.57 (vedere tabella Appendice 2) per cui esce dall’intervallo ricavato dalle tabelle dl-du (1.55-1-62): assenza di correlazione interna. la statistica di LIN-MUDHOLKAR, per la gaussiana, per alfa=0.05 e r=+/- 0.403 ricavato dalle tabelle, ha il valore -0.0416, cioè cade all’interno dell’intervallo di r, per cui non posso rifiutare l’ipotesi nulla: la distribuzione dei residui così calcolati è da considerarsi gaussiana. Forse è proprio l’effetto di non aver esplicitata la serie CLTR con il calcolo del TREND a favorire la compatibilità dei residui alle ipotesi iniziali.

MODELLO DI REGRESSIONE LINEARE SEMPLICE (RLS) E TESTS RELATIVI.

ADEGUAMENTO DEL MODELLO DI REGRESSIONE ALLA POPOLAZIONE. COEFFICIENTI DELLA RETTA ED R-q

TEST SU R-q E LA F DI FISHER , TESTS SUI COEFFICIENTI DELLA RETTA, INTERVALLO DI CONFIDENZA.

RESIDUO DELLA REGRESSIONE E L’AFFIDABILITA’.

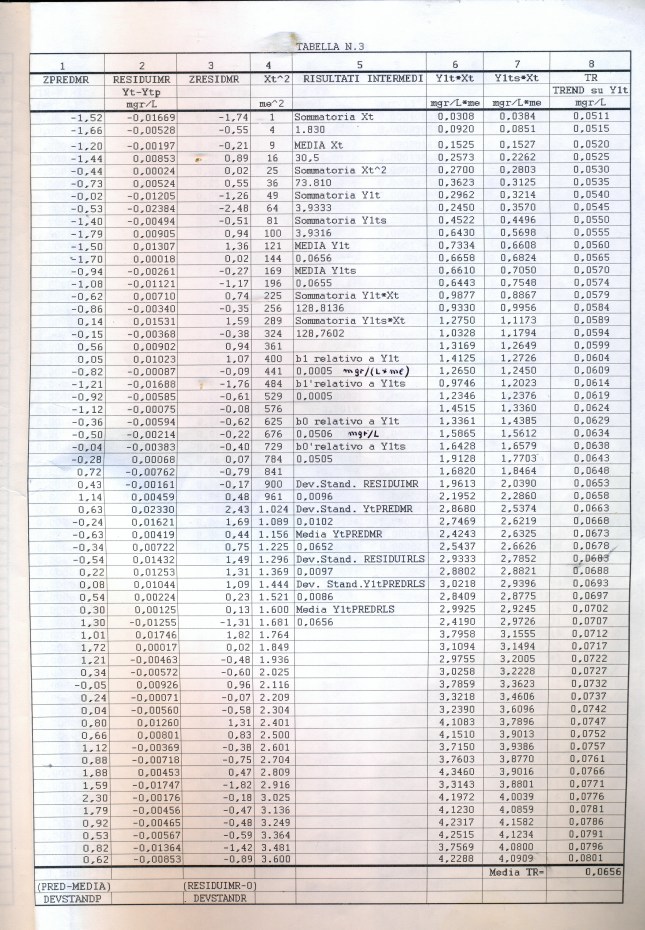
Applichiamo invece a y1t o y1ts (APPENDIX3, TABELLA N.2, col.2; TABELLA N.2, col.3) ) un modello di regressione per separare il TREND dai loro contenuti. Proviamo una regressione lineare con la sola variabile, il tempo, misurato in mesi (un solo regressore, k1=1 nelle tabelle DW), senza preoccuparci per ora se tale modello sia idoneo. Lo controlleremo dall’analisi dei residui. Se sono rispettate le assunzioni di linearità, una buona misura dell’adeguamento del modello lineare ai dati è il Coefficiente di Determinazione R-quadro. La sua radice quadrata R è il Coefficiente di correlazione di Pearson detto anche Multiple-R. Se R-q è 1, significa che tutte le osservazioni cadono sulla retta di regressione; se zero, nessuna associazione lineare fra le variabili, anche se può esserci una relazione non lineare. R-q può così essere interpretato come la proporzione della variazione di y ‘spiegata’ dal modello , come precisato in altre occasioni. Su y1t o su y1ts, si opera con una regressione lineare calcolando bo e b1 ed ottenendo in ambedue i casi, come era prevedibile, differendo le due serie per la sola componente casuale, la stessa retta di regressione seguente (APPENDIX3, TABELLA N.3, col.8 e APPENDIX3, TABELLA N.4, col.3 per i valori previsti):

y_predetto = TREND = TREND’ = 0.051 + 0.00005*t

Vedere APPENDIX3, TABELLA N.3, col.5, per i risultati intermedi al fine del cacolo dei coefficienti della retta.

Nel nostro caso R-q = 0.44, cioè il modella spiega il 44% della variazione complessiva della variabile dipendente. Per controllare l’ipotesi nulla che nella popolazione non esista relazione lineare (R-q_pop.=0), si procede con l’analisi della varianza. Per tutti i particolari dei ‘conti’ che seguono vedere, per es., il Post ‘Un percorso verso il periodogramma’ su questo stesso BLOG. Seguendo le indicazioni riportate nel paragrafo relativo a questo argomento nel Post su nominato, si ottiene la seguente tabella:

GL SOMMA DEI QUADRATI MEAN SQUARE

Variazione di regressione 1 0.00435 0.00435

Variazione residuale 58 0.00559 0.000096

TOT 0.00994

da cui: Somma quadrati reg./Somma quadrati tot = 0.44, cioè R-quadro.

La statistica F di Fisher che permette di saggiare l’ipotesi nulla: R-quadro pop.=0, è 0.00435/0.000096 = 45.31, da cui, riportata sulle tavole con 1 e 58 gradi di libertà (GL), si ricava una significanza per F minore di 0.00001, per cui si respinge l’ipotesi nulla e nella popolazione esisterà con alta probabilità una relazione lineare.

Procedendo ancora a prove incrociate si può testare l’ipotesi che b1_pop. =0; si calcola la statistica T per b1: pendenza/errore standard_pend, ottenendo ERb1=7.31*10^-5 perché b1=0.000492, risulta T=6.73, che dalle tabelle relative per 58 gradi di libertà (GL=N-2) si ha una significanza per T di 0.0000..<<0.05, per cui si respinge l’ipotesi nulla che la pendenza della popolazione sia zero (quindi esiste dipendenza lineare).

Procedendo, nell’intervallo di confidenza al 95% per la pendenza non potrà allora il valore zero. Infatti calcolando ESb1 come suggerito da altri interventi (0.000073), l’intervallo di confidenza al 95% per beta1 risulta (con 58 GL):

b1-1.96*ESb1 <= beta1 <= b1+ 1.96*ESb1

0.00492-0.00014 <= beta1 <= 0.00492+0.00014

0.00035 <= beta1 <=0.00063

Si vede chiaramente come i vari tests, se affidabili, confermano la presenza di un trend lineare nei dati.

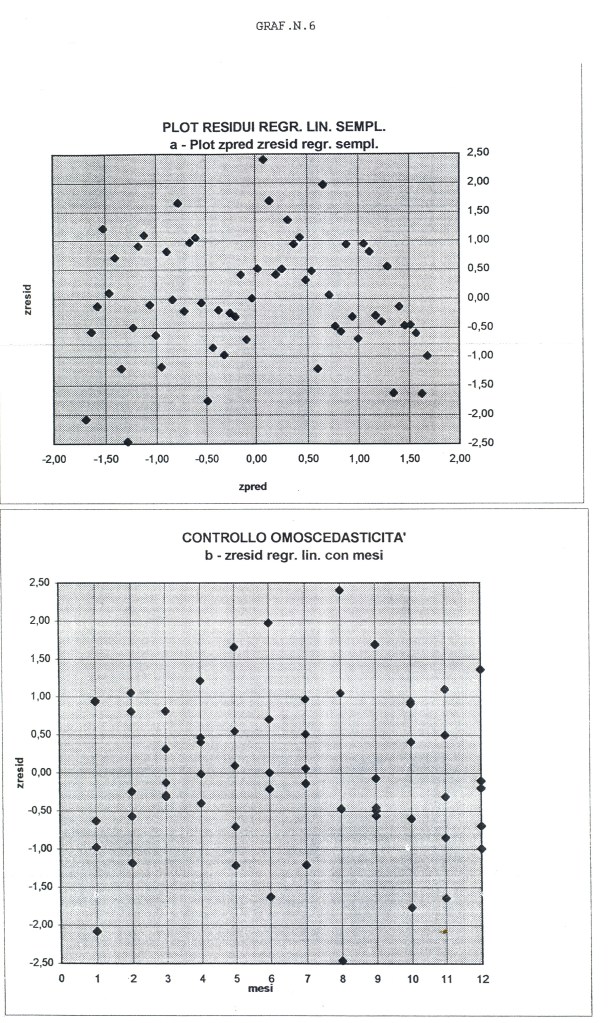
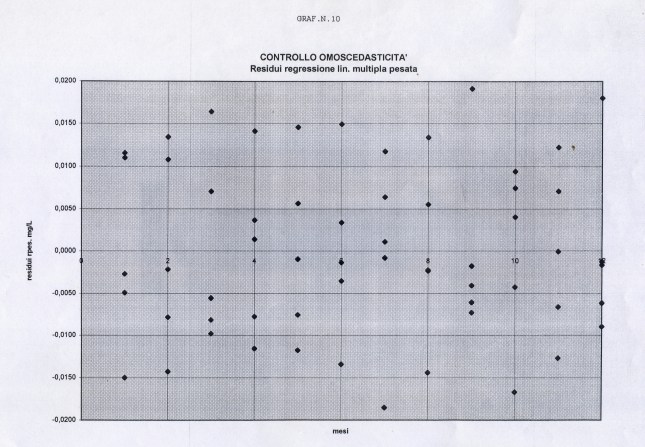
Togliendo da y1t la serie del trend, si otterrà la serie CLRD ( APPENDIX3, TABELLA N.4, col.4) con l’eventuale ciclo + la componente casuale (random) I residui della regressione, per il modo con cui abbiamo proceduto, sono proprio i valori della serie CLRD. E’ prevedibile che questa serie, se davvero includerà una componente ciclica significativa,non risulterà rispetterà almeno qualche condizione fra quelle ipotizzate sui residui (indipendenza, varianza costante…). procederemo ad investigare questa serie sui residui. Applicando ad essi il programma CORR, otteniamo il grafico, GRAF. N.5 a) correlogramma) e 5b (periodogramma), il test per l’indipendenza di Durbin Watson e quello per la normalità di Lin Mudholkar. Il valore di DW è risultato 1.378, che (N=60, K’=1 e alfa =0.05) esce a sinistra dell’intervallo 1.55-1.62 e quindi l’autocorrelazione è positiva, mentre il test per la gaussiana (rischio 0.05, N=60, r=+/-0.403, fornisce rc=-0.0298, cioè all’inteno dell’intervallo, per cui non posso rifiutare l’ipotesi nulla (la serie ha distribuzione gaussiana). Graficando i residui standardizzati con la variabile pred pure standardizzata, si ottiene il GRAF. N. 6 a dove non appaiono patterns evidenti. Dal GRAF. N.6 b invece, ottenuto riportando i residui per ogni unità di tempo, si evidenzia una qualche variazione della varianza dei residui (eteroscedasticità, variazione a clessidra). Allora i tests che fanno riferimento al comportamento della popolazione universo (in particolare gli F-tests) possono non essere affidabili e quindi incerto il modello di regressione usata.

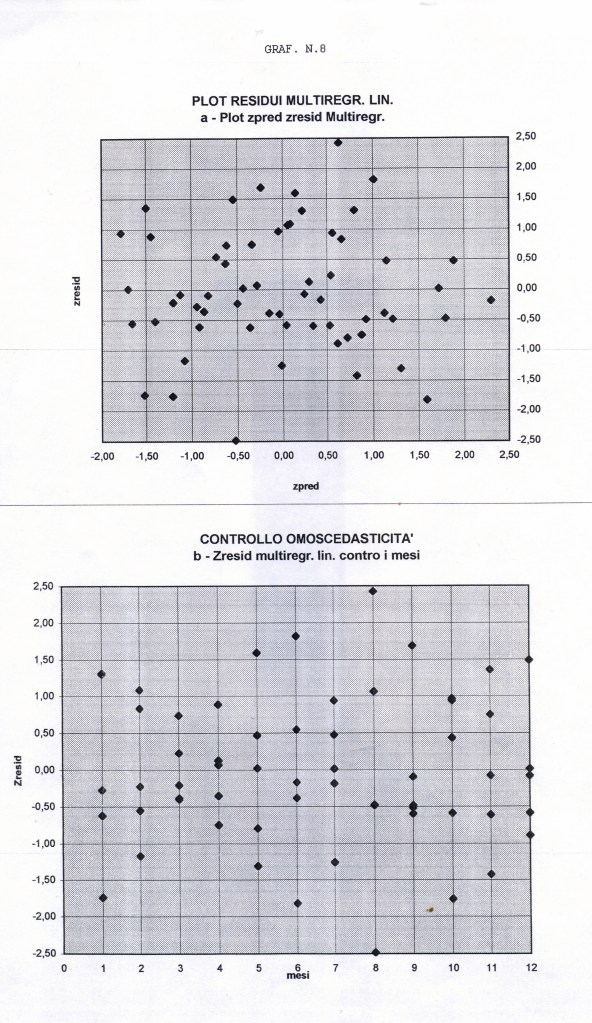
Al termine dell’analisi con un modello di regressione lineare semplice, tenteremo ulteriori approfondimenti alla ricerca di un maggiore R-quadro, ma specialmente di una maggior concordanza dei residui alle condizioni iniziali (linearità, normalità, indipendenza, omoscedasticità).

10 – SECONDA PARTE IN SINTESI

SECONDA PARTE IN SINTESI: UN ALTRO TENTATIVO SULLA CACCIA AI RESIDUI (senza passare attraverso una regresssione)

SCRIPTS IN BLOCCO NOTE: DA COPIARE DIRETTAMENTE SULLA CONSOLLE DI R

# Intanto trascriviamo nel vettore yt i 60 dati della conc. As da cui partire. Impariamo poi a calcolare con R gli altri 5 vettori dati che faranno parte dell'analisi della nostra serie
# reale e quindi della nostra esercitazione. Calcoliamo come primo vettore Mt (media mobile di ordine  12 su yt.

yt=c(.033,.043,.051,.059,.061,.063,.053,.036,.046,.056,.063,.048,.053,.043,.066,.053,.082,.06,.08,.076,.056,.036,.05,
.053,
.056,.058,.061,.063,.065,.068,.0815,.095,.079,.063,.069,.074,.08,
.0765,.073,.0695,.066,.093,.083,.073,.063,.074,.067,.06,.086,.08,.073,.067,.089,.064,.087,.079,.07,.065,.06,.063)

t=1

#Come primo passo grafichiamo i dati e osserviamo se ci sono regolarità all'interno (trend, oscillazioni), precisiamo le ipotesi con un correlogramma ed un periodogramma, I dati sono mensili: Ipotizziamo comunque una oscillazione di periodo 12.

# Calcoliamo, come primo vettore, Mt (media mobile centrata e pesata di ordine 12 su yt).

yt=as.vector(yt) ; n=length(yt); Mt=c()
for(t in 7:n){Mt[t] = (yt[t-6]/2+yt[t-5]+yt[t-4]+yt[t-3]+yt[t-2]+
yt[t-1]+yt[t]+yt[t+1]+yt[t+2]+yt[t+3]+yt[t+4]+yt[t+5]+(yt[t+6])/2)/12}
Mtc=Mt[7:54]

mt=filter(yt,filter=rep(1/13,13))
# calcolo della Mm col comando filter di R: confrontare i due risultati
mt #OK

# in Mt ci sono i 48 (60-12) dati Media mobile di yt, da cui costruisco i 12 Fattori Stagionali (FStag) 
facendo la media dei 4 gennaio, dei 4 febbraio ecc. a partire da luglio, perchè Mt iniziava con luglio.
FSTag0 = matrix(Mtc, ncol=12, byrow=T)
# matrice di 4 righe (valori dei 12 mesi dei 4 anni) e 12 colonne con in ognuna le 4 conc. dei mesi dello stesso nome a partire da un luglio.
FStag1=colMeans(FSTag0)
#  in FStag1 trovo le 12 medie dei 4 mesi dello stesso nome (inizio luglio, fine giugno)
FStag=c(FStag1[7:12], FStag1[1:6]) # da controllare! Ordino da gennaio. OK
ESAs=rep(FStag,5) # EFFETTO STAGIONALE As
ESAs # 60 dati
Yt1=yt-ESAs # Ciclo+Trend+Random
Yt1 # 60 dati
Yt1c=Yt1[3:58]
Yt1s=c()
for(i in 1:60){Yt1s[i]=(Yt1[i-2]+2*Yt1[i-1]+3*Yt1[i]+2*Yt1[i+1]+
Yt1[i+2])/9}
Yt1s=as.vector(Yt1s) # smusso Yt1 con Mm 3*3

ns=length(Yt1s) # più corto di 4 elementi
Yt1s # yt1 senza random; cioè Ciclo+Trend

par(ask=T)

Yt1s=Yt1s[3:(ns-2)]

RD=Yt1c-Yt1s # forse si tratta solo di random: il Ciclo?

#Riportiamo in una tabella 1 5 vettori dell'analisi su yt

#data <- data.frame(t,yt,ESAs,Yt1,RD)

# Facciamo i 5 correlogrammi dei vettori trovati: yt, ESAs, Yt1, Yt1s, RD
coyt=acf(yt)
coyt
coESAs=acf(ESAs)
coESAs
coYt1=acf(Yt1)
coYt1s=acf(Yt1s)
coYt1s
coRD=acf(RD)
coRD
# Interessante abbinare il correlogramma con il periodogramma e da controllare i correlogrammi con il programmino scritto dall'autore


RISULTATI DEL PROGRAMMA PRECEDENTE (come si vede gira senza errori!)


> # Interessante abbinare il correlogramma con il periodogramma.
> # Intanto trascriviamo nel vettore yt i 60 dati della conc. As da cui partire. Impariamo poi a calcolare con R gli altri 5 vettori dati che faranno parte dell'analisi della nostra serie
 # reale e quindi della nostra esercitazione. Calcoliamo come primo vettore Mt (media mobile di ordine  12 su yt.

> 
> yt=c(.033,.043,.051,.059,.061,.063,.053,.036,.046,.056,.063,.048,.053,.043,.066,.053,.082,.06,.08,.076,.056,.036,.05,
+ .053,
+ .056,.058,.061,.063,.065,.068,.0815,.095,.079,.063,.069,.074,.08,
+ .0765,.073,.0695,.066,.093,.083,.073,.063,.074,.067,.06,.086,.08,.073,.067,.089,.064,.087,.079,.07,.065,.06,.063)
> 
> t=1
> 
> #Come primo passo grafichiamo i dati e osserviamo se ci sono regolarità all'interno (trend, oscillazioni), precisiamo le ipotesi con un correlogramma ed un periodogramma, I dati sono mensili: Ipotizziamo comunque una oscillazione di periodo 12.
> 
> # Calcoliamo, come primo vettore, Mt (media mobile centrata e pesata di ordine 12 su yt).
> 
> yt=as.vector(yt) ; n=length(yt); Mt=c()
> for(t in 7:n){Mt[t] = (yt[t-6]/2+yt[t-5]+yt[t-4]+yt[t-3]+yt[t-2]+
+ yt[t-1]+yt[t]+yt[t+1]+yt[t+2]+yt[t+3]+yt[t+4]+yt[t+5]+(yt[t+6])/2)/12}
> Mtc=Mt[7:54]
> 
> mt=filter(yt,filter=rep(1/13,13)) # 13 o 12?
> # calcolo della Mm col comando filter di R: confrontare i due risultati
> mt #OK
Time Series:
Start = 1 
End = 60 
Frequency = 1 
 [1]         NA         NA         NA         NA         NA         NA
 [7] 0.05115385 0.05192308 0.05369231 0.05384615 0.05561538 0.05553846
[13] 0.05684615 0.05861538 0.06015385 0.05938462 0.05892308 0.05815385
[19] 0.05876923 0.05915385 0.06053846 0.06030769 0.06123077 0.06015385
[25] 0.06180769 0.06296154 0.06319231 0.06373077 0.06626923 0.06811538
[31] 0.07019231 0.07176923 0.07292308 0.07357692 0.07380769 0.07596154
[37] 0.07711538 0.07646154 0.07400000 0.07361538 0.07392308 0.07323077
[43] 0.07415385 0.07415385 0.07388462 0.07342308 0.07492308 0.07476923
[49] 0.07430769 0.07400000 0.07376923 0.07392308 0.07284615 0.07253846
[55]         NA         NA         NA         NA         NA         NA
> 
> # in Mt ci sono i 48 (60-12) dati Media mobile di yt, da cui costruisco i 12 Fattori Stagionali (FStag) facendo la media dei 4 gennaio, dei 4 febbraio ecc. a partire da luglio, perchè Mt iniziava con luglio.
> FSTag0=matrix(Mtc, ncol=12, byrow=T)
> # matrice di 4 righe (valori dei 12 mesi dei 4 anni) e 12 colonne con in ognuna le 4 conc. dei mesi dello stesso nome a partire da un luglio.
> FStag1=colMeans(FSTag0)
> #  in FStag1 trovo le 12 medie dei 4 mesi dello stesso nome (inizio luglio, fine giugno)
> FStag=c(FStag[7:12], FStag1[1:6]) # da controllare! Ordino da gennaio. OK
> ESAs=rep(FStag,5) # EFFETTO STAGIONALE As
> ESAs # 60 dati
 [1] 0.06147115 0.06221154 0.06285577 0.06317308 0.06323077 0.06334615
 [7] 0.05878846 0.05965385 0.06022115 0.06050962 0.06085577 0.06113462
[13] 0.06147115 0.06221154 0.06285577 0.06317308 0.06323077 0.06334615
[19] 0.05878846 0.05965385 0.06022115 0.06050962 0.06085577 0.06113462
[25] 0.06147115 0.06221154 0.06285577 0.06317308 0.06323077 0.06334615
[31] 0.05878846 0.05965385 0.06022115 0.06050962 0.06085577 0.06113462
[37] 0.06147115 0.06221154 0.06285577 0.06317308 0.06323077 0.06334615
[43] 0.05878846 0.05965385 0.06022115 0.06050962 0.06085577 0.06113462
[49] 0.06147115 0.06221154 0.06285577 0.06317308 0.06323077 0.06334615
[55] 0.05878846 0.05965385 0.06022115 0.06050962 0.06085577 0.06113462
> Yt1=yt-ESAs # Ciclo+Trend+Random
> Yt1 # 60 dati
 [1] -0.0284711538 -0.0192115385 -0.0118557692 -0.0041730769 -0.0022307692
 [6] -0.0003461538 -0.0057884615 -0.0236538462 -0.0142211538 -0.0045096154
[11]  0.0021442308 -0.0131346154 -0.0084711538 -0.0192115385  0.0031442308
[16] -0.0101730769  0.0187692308 -0.0033461538  0.0212115385  0.0163461538
[21] -0.0042211538 -0.0245096154 -0.0108557692 -0.0081346154 -0.0054711538
[26] -0.0042115385 -0.0018557692 -0.0001730769  0.0017692308  0.0046538462
[31]  0.0227115385  0.0353461538  0.0187788462  0.0024903846  0.0081442308
[36]  0.0128653846  0.0185288462  0.0142884615  0.0101442308  0.0063269231
[41]  0.0027692308  0.0296538462  0.0242115385  0.0133461538  0.0027788462
[46]  0.0134903846  0.0061442308 -0.0011346154  0.0245288462  0.0177884615
[51]  0.0101442308  0.0038269231  0.0257692308  0.0006538462  0.0282115385
[56]  0.0193461538  0.0097788462  0.0044903846 -0.0008557692  0.0018653846
> Yt1c=Yt1[3:58]
> Yt1s=c()
> for(i in 1:60){Yt1s[i]=(Yt1[i-2]+2*Yt1[i-1]+3*Yt1[i]+2*Yt1[i+1]+
+ Yt1[i+2])/9}
> Yt1s=as.vector(Yt1s) # smusso Yt1 con Mm 3*3
> 
> ns=length(Yt1s) # più corto di 4 elementi
> Yt1s # yt1 senza random; cioè Ciclo+Trend
 [1]            NA            NA -1.255983e-02 -6.694444e-03 -3.708333e-03
 [6] -4.989316e-03 -9.090812e-03 -1.287073e-02 -1.140385e-02 -8.274573e-03
[11] -5.727564e-03 -8.419872e-03 -9.424145e-03 -1.017735e-02 -4.337607e-03
[16] -1.027778e-03  5.958333e-03  8.455128e-03  1.157585e-02  6.129274e-03
[21] -2.070513e-03 -1.060791e-02 -1.194979e-02 -9.530983e-03 -5.979701e-03
[26] -3.955128e-03 -2.004274e-03 -2.777778e-05  3.902778e-03  1.089957e-02
[31]  1.874252e-02  2.179594e-02  1.809615e-02  1.216987e-02  1.027244e-02
[36]  1.208013e-02  1.424252e-02  1.326709e-02  1.032906e-02  9.861111e-03
[41]  1.273611e-02  1.806624e-02  1.824252e-02  1.524038e-02  1.026282e-02
[46]  7.836538e-03  7.827991e-03  9.913462e-03  1.368697e-02  1.393376e-02
[51]  1.377350e-02  1.130556e-02  1.384722e-02  1.478846e-02  1.779808e-02
[56]  1.546261e-02  1.159615e-02  5.836538e-03            NA            NA
> 
> par(ask=T)
> 
> Yt1s=Yt1s[3:(ns-2)]
> 
> RD=Yt1c-Yt1s # forse si tratta solo di random: il Ciclo?
> 
> #Riportiamo in una tabella 1 5 vettori dell'analisi su yt
> 
> #data <- data.frame(t,yt,ESAs,Yt1,RD)
> 
> # Facciamo i 5 correlogrammi dei vettori trovati: yt, ESAs, Yt1, Yt1s, RD
> coyt=acf(yt)
Aspetto per confermare cambio pagina...
> coyt


Autocorrelations of series ‘yt’, by lag

     0      1      2      3      4      5      6      7      8      9     10 
 1.000  0.541  0.395  0.223  0.302  0.221  0.330  0.281  0.150  0.102  0.150 
    11     12     13     14     15     16     17 
 0.248  0.255  0.308  0.197  0.099 -0.006  0.042 
> coESAs=acf(ESAs)
Aspetto per confermare cambio pagina...
> coESAs

Autocorrelations of series ‘ESAs’, by lag

     0      1      2      3      4      5      6      7      8      9     10 
 1.000  0.542  0.187 -0.111 -0.349 -0.460 -0.455 -0.423 -0.309 -0.102  0.146 
    11     12     13     14     15     16     17 
 0.433  0.800  0.434  0.150 -0.088 -0.276 -0.362 
> coYt1=acf(Yt1)
Aspetto per confermare cambio pagina...
> coYt1s=acf(Yt1s)
Aspetto per confermare cambio pagina...
> coYt1s

Autocorrelations of series ‘Yt1s’, by lag

    0     1     2     3     4     5     6     7     8     9    10    11    12 
1.000 0.908 0.757 0.610 0.519 0.457 0.396 0.326 0.271 0.256 0.277 0.317 0.335 
   13    14    15    16    17 
0.321 0.263 0.198 0.145 0.123 
> coRD=acf(RD)
Aspetto per confermare cambio pagina...
> coRD

Autocorrelations of series ‘RD’, by lag

     0      1      2      3      4      5      6      7      8      9     10 
 1.000 -0.308 -0.166 -0.187  0.222 -0.198  0.195  0.066 -0.089 -0.097  0.014 
    11     12     13     14     15     16     17 
 0.004 -0.029  0.147  0.043 -0.114 -0.071  0.046 
> # Interessante abbinare il correlogramma con il periodogramma: da fare.

L’EPILOGO

SEGUONO ULTERIORI APPROFONDIMENTI: 

APPLICAZIONE DI UNA REGRESSIONE LINEARE MULTIPLA (RLM) OPPORTUNA (variabili "dummy").
 
COME CALCOLARE LA F DI FISHER NELLE REGRESSIONI RLM.
 
COME CALCOLARE L'ERRORE STANDARD SUI COEFFICIENTI DI REGRESSIONE NELLA RML
 
COME SI APPLICA UNA REGRESSIONE LINEARE MULTIPLA PESATA (RLMP)
 
CHI VOLESSE ESERCITARSI SU ESEMPI RELATIVI AL CALCOLO MATRICIALE APPLICATO ALL'ANALISI DI DATI    SPERIMENTALI CERCARE IN QUESTO SITO "TIPS DI SCIENZA" (in particolare sui "conti" relativi alla   regressione lineare multipla (MLR). 
LO SCRITTO CHE SEGUE E' L'ULTIMA TRANCE DELL'ARTICOLO ORIGINALE CHE RIGUARDA GLI ULTERIORI        APPROFONDIMENTI,ELENCATI SOPRA, SCRITTO ANCORA DALLO SCRIVENTE, RIVISITATO E INTERPRETATO CON R   IN QUESTO POST. I RIFERIMENTI COME 1.1.2.2 ECC. RIGUARDANO RIMANDI A SUOI PARAGRAFI SPECIFICI. DATA LA NATURA A 'ZIBALDONE LEOPARDIANO DISPERSO' DI QUESTO LAVORO A GETTO ROBINSONIANO CI PROPONIAMO DI INSERIRE LA SECONDA PARTE DELL'ORIGINALE PRIMA DELLE APPENDICI. DOVREMMO SCANNERIZZARLO MEGLIO! 

11-L'EPILOGO

GRAF. N.9

12 -APPENDICE1

APPENDICE1

Il correlogramma ed il test di Durbin-Watson. ([3], 949-953)

Ammettiamo che il lettore conosca il Coefficiente di Correlazione lineare di Pearson, ovvero date N paia di osservazioni su due variabili X e Y, tale Coefficiente di Correlazione fra esse e dato:

r = Σi(Xi- Xm)*(Yi – Ym)/SQR[ Σi(Xi-Xm)^2 * Σi(Yi – Ym)]

Quest’idea viene trasferita alle serie storiche per vedere se osservazioni successive sono correlate.

Date N osservazioni X1, X2,………Xn , in una serie storica discreta possiamo considerare N-1 paia di osservazioni (X1,X2), (X2,X3), . . . ,(X(n-1),Xn), le cui prime osservazioni di ogni paio costituiscono la prima variabile e le seconde, la seconda variabile. Se si applica la formula precedente, dove Xi sarebbe Xt e Yi sarebbe Y(t+1), mentre Xm sarebbe la media della prima variabile (da t=1 a t=N-1) e Ym sarebbe la media della seconda variabile (da t=2 a t=N, in ambedue i casi il numero degli elementi sarebbe N-1. Si otterrebbe una formula complessa con due medie diverse che vengono invece calcolate ambedue sulla serie originaria di numerosita N. Si usa cosi la formula approssimata scritta sotto, estesa al caso in cui si voglia trovare la correlazione tra serie di osservazioni a distanza H fra loro (slittate di h termini o di lag h)

I coefficienti di auto-correlazione r_h, dove h=0,1,2…q e q è minore ad uguale a (N-2)/2, sono coefficienti di correlazione, calcolati per ogni valore di h, che misurano la concordanza o la discordanza tra i valori di una serie storica e quelli della stessa però slittati di h unità di tempo (lag h), consentendo di analizzare la sua struttura interna, ossia i legami fra i termini della stessa ([8] 18-20).

rh = Σi[(y(t)-ym)(y(t+h)-ym)]/[(n-h)*Σj(y(t)-ym)^2/n)] dove i va da t=1…n-h e j va da t=1 … n

in alcuni testi viene abolito il fattore n/(n-h).

Tale formula presenta la semplificazione di poter utilizzare una media unica per le Yt (quella dei dati originali), presupponendo una situazione stazionaria ([8] pag.19 e [2] pag.133). In particolare r0 = 1 (lag h =0, nessun slittamento) e gli altri r_hassumono valori fra +1 (completa concordanza) e -1 (totale discordanza). Il correlogramma è la rappresentazione grafica dei coefficienti di auto-correlazione in funzione degli slittamenti (lags h) e permette di vedere se la serie storica possiede qualche regolarità interna.

CENNI DI LETTURA DEI CORRELOGRAMMI

-I coeff. di autocorr. di dati random hanno distribuzione campionaria che può essere approssimata da una curva gaussiana con media zero ed errore standard 1//N. Questo significa che il 95% di tutti i coeff. di autocorr. , calcolati da tutti i possibili campioni estratti, dovrebbero giacere entro un range specificato da: zero +/- 1.96 errori standard. I dati cioè della serie saranno da considerarsi random se questi coefficienti saranno entro i limiti:

-1.96 (1/√n)≤ r_{h ≤} +1.96 (1/√n); la fascia dell’errore: +/- 2/√n

Per l’interpretazione dei correlogrammi vedere ([8] 20-25) da cui ricaviamo le seguenti informazioni.

– Una serie storica completamente casuale, cioè i cui successivi valori sono da considerarsi tutti indipendenti fra loro (non correlati), tutti i valori di r_h (eccetto r0 che è sempre +1, correlazione della serie con se stessa) oscilleranno accidentalmente intorno allo zero entro la fascia dell’errore. Se l’idea iniziale era questa in effetti 5 su 100 valori di rh potrebbero superare la fascia dell’errore e se plotto il correlogramma, 19 su 20 valori di rh potrebbero cadere all’interno della fascia, ma ci si potrebbe aspettare che uno possa eesere significativo sulla media. Insomma anche se la serie è casuale, ogni tanto verso lag più elevati potrebbero apparire picchi significativi. Se abbiamo a che fare con un numero elevato di coefficienti, potrebbero apparire risultati non aspettati. Questo rende il correlogramma uno strumento di investigazione incerto.

– I coeff. di autocorr. per i dati stazionari (assenza di TREND) vanno velocemente a zero dopo il 4° o 5° lag di tempo e sono significativamente diversi da zero per i primi lag. Anche su correlogrammi, ai lags più bassi, si possono notare coefficienti di autocorrelazione positivi rapidamente decrescenti e per i lag successivi oscillazioni intorno allo zero. Ciò significa che esiste nella serie una persistenza di valori a breve termine, nel senso che se la grandezza in studio ha valore più elevato della media in un mese, lo sarà anche in uno o due mesi successivi e così per valori inferiori alla media.

-Se la serie storica presenta oscillazioni, anche il correlogramma tende ad assumere valori positivi e negativi, oscillando con lo stesso periodo della serie fino a smorzarsi ai lags più elevati. Se es. esiste un componente stagionale di periodo 12 mesi, nei dintorni del coefficiente di lag 12 ci sarà una zona significativamente diversa da zero.

– Nelle serie non stazionarie (presenza di TREND) i valori di rh non scendono velocemente a zero, ma si mantengono significativi per più valori del lag e solo se l’effetto del TREND è paragonabile alle altre eventuali relazioni presenti nei dati è possibile intuirle nel grafico (GRAFICO. N.2)

IL TEST DI DURBIN WATSON

Così la lettura dei correlogrammi talora può risultare ardua. Un modo veloce, affidabile e quantitativo per testare l’ipotesi che esista all’interno di una serie storica correlazione fra i suoi termini, cioè i termini non siano indipendenti, è somministrare alla serie il test di Durbin Watson ([8] 18-20), la cui statistica è espressa dalla formula:

d =∑ (e_i – e_i-1)² /∑ ei²

La sommatoria al numeratore inizia dal 2° termine (i=2) e coinvolge ni termini . La statistica d varia da 0 a 4 e quando l’ipotesi nulla è vera (autocorrelazione assente) d dovrebbe essere vicino a 2. Il test permette di decidere di respingere l’ipotesi nulla, di accettarla o essere inconclusivo. Utilizzando la tabella opportuna (allegata a queste note) si ottengono i valori critici di dl e du che servono per la decisione: all’interno dell’intervallo dl-du, la situazione è incerta; a sinistra di dl , si respinge l’ipotesi nulla. Vedremo in seguito come si calcola d con R e come si usa la tabella.

Il programma CORR, scritto in Qbasic, riportato in nota, permette il calcolo dei coefficienti di autocorrelazione con l’errore (un qualsiasi programma di grafica permetterà di costruire il correlogramma) e il calcolo della statistica di D. W. Abbiamo già visto (vedere programminosul correlogramma) come operare anche con il linguaggio R.

13 – APPENDICE2

APPENDICE2

Programmi in Qbasic e tabelle

PROGRAMMA CORR (coefficienti di autocorrelazione, il test di Durbin Watson, il test di Lin Mudholkar, Analisi spettrale per il periodogramma

GRAF. N.9

14 – APPENDICE3

APPENDIX3

TABELLE DEI RISULTATI

15 – APPENDICE4

APPENDIX4

ANALISI, CON IL LINGUAGGIO R, DELLA SERIE STORICA TRIMESTRALE RIVISITATA E AMPLIATA CON PERIODOGRAMMI E RISULTATI

period_det_trim3

DA CAMBIARE:

> rm(list=ls(all=TRUE))
> #SCRIPTS IN R
>
> library(graphics)
> library(tseries)

‘tseries’ version: 0.10-32

‘tseries’ is a package for time series analysis and computational
finance.

See ‘library(help=”tseries”)’ for details.

> library(stats)
> #library(UsingR)
> library(lattice)
> library(lmtest)
Carico il pacchetto richiesto: zoo

Attaching package: ‘zoo’

The following objects are masked from ‘package:base’:

as.Date, as.Date.numeric

>
> w=c(0.033,0.043,0.051,0.059,0.061,0.063,0.053,0.036,0.046,0.056,0.063,0.048,0.053,0.043,
+ 0.066,0.053,0.082,0.06,0.08,0.076,0.056,0.036,0.05,0.053,0.056,0.058,0.061,0.063,0.065,
+ 0.068,0.0815,0.095,0.079,0.063,0.069,0.074,
+ 0.08,0.0765,0.073,0.0695,0.066,0.093,0.083,
+ 0.073,0.063,0.074,0.067,0.06,0.086,0.08,0.073,0.067,0.089,0.064,0.087,0.079,0.07,0.065,0.06,.063)
>
> par(ask=T)
>
> par(mfrow=c(1,3))
>
> trim=matrix(w,ncol=3,byrow=T)
>
>
> medietrim=rowMeans(trim)
>
> medietrim
[1] 0.04233333 0.06100000 0.04500000 0.05566667 0.05400000 0.06500000
[7] 0.07066667 0.04633333 0.05833333 0.06533333 0.08516667 0.06866667
[13] 0.07650000 0.07616667 0.07300000 0.06700000 0.07966667 0.07333333
[19] 0.07866667 0.06266667
>
> # FIG.1
> ts.plot(medietrim,type=”l”,main=”FIG.1″) #finchè non lo sostituisco posso usare abline
Aspetto per confermare cambio pagina…
>
> w1=c(1:20)
> regtrim=lm(medietrim~w1)
> abline(regtrim)
>
> summary(regtrim)

Call:
lm(formula = medietrim ~ w1)

Residuals:
Min 1Q Median 3Q Max
-0.015979 -0.005078 0.001069 0.006031 0.019235

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0503921 0.0041790 12.058 4.67e-10 ***
w1 0.0014127 0.0003489 4.049 0.000752 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.008996 on 18 degrees of freedom
Multiple R-squared: 0.4767, Adjusted R-squared: 0.4476
F-statistic: 16.4 on 1 and 18 DF, p-value: 0.0007524

>
> val_pred_w=predict(regtrim) #calcolo i 20 valori predetti dalla prima regressione
> length(val_pred_w)
[1] 20
>
>
> detrend_trim=medietrim-val_pred_w
> detrend_trim
1 2 3 4 5
-0.0094714286 0.0077825815 -0.0096300752 -0.0003760652 -0.0034553885
6 7 8 9 10
0.0061319549 0.0103859649 -0.0153600251 -0.0047726817 0.0008146617
11 12 13 14 15
0.0192353383 0.0013226817 0.0077433584 0.0059973684 0.0014180451
16 17 18 19 20
-0.0059946115 0.0052593985 -0.0024865915 0.0014340852 -0.0159785714
>
> #FIG.2
> plot(detrend_trim,type=”l”, main=”FIG.2″)
>
>
> detrend_trim
1 2 3 4 5
-0.0094714286 0.0077825815 -0.0096300752 -0.0003760652 -0.0034553885
6 7 8 9 10
0.0061319549 0.0103859649 -0.0153600251 -0.0047726817 0.0008146617
11 12 13 14 15
0.0192353383 0.0013226817 0.0077433584 0.0059973684 0.0014180451
16 17 18 19 20
-0.0059946115 0.0052593985 -0.0024865915 0.0014340852 -0.0159785714
>
> trim1=matrix(detrend_trim,ncol=4,byrow=T)
> medietrim1=colMeans(trim1)
> medietrim1_5anni=rep(medietrim1,5)
>
> #FIG.3
> plot(medietrim1_5anni,type=”l”,main=”FIG.3″)
>
> medietrim1_5anni
[1] -0.0009393484 0.0036479950 0.0045686717 -0.0072773183 -0.0009393484
[6] 0.0036479950 0.0045686717 -0.0072773183 -0.0009393484 0.0036479950
[11] 0.0045686717 -0.0072773183 -0.0009393484 0.0036479950 0.0045686717
[16] -0.0072773183 -0.0009393484 0.0036479950 0.0045686717 -0.0072773183
>
> par(mfrow=c(2,2))
>
> #FIG.4
> acf(medietrim1_5anni,main=”FIG.4″)
Aspetto per confermare cambio pagina…
>
> valAdjtrim=medietrim-medietrim1_5anni #trend_ random
>
>
> fitadj_trim=lm(valAdjtrim~w1)
>
> fitadj_trim

Call:
lm(formula = valAdjtrim ~ w1)

Coefficients:
(Intercept) w1
0.049678 0.001481

>
> summary(fitadj_trim)

Call:
lm(formula = valAdjtrim ~ w1)

Residuals:
Min 1Q Median 3Q Max
-0.0136886 -0.0044597 -0.0006167 0.0058313 0.0146327

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.049678 0.003486 14.251 3.03e-11 ***
w1 0.001481 0.000291 5.088 7.67e-05 ***
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.007504 on 18 degrees of freedom
Multiple R-squared: 0.5899, Adjusted R-squared: 0.5671
F-statistic: 25.89 on 1 and 18 DF, p-value: 7.671e-05

>
> #FIG.5
> plot(valAdjtrim,type=”l”,main=”FIG.5″)
> abline(fitadj_trim)
>
> #ANALISI RESIDUI
>
>
> dwtest(fitadj_trim, alternative=”two.sided”)

Durbin-Watson test

data: fitadj_trim
DW = 1.9024, p-value = 0.6301
alternative hypothesis: true autocorrelation is not 0

> #forse potremo interpolare l’elemento 11
>
> #FIG.6
> res=resid(fitadj_trim)
> plot(res,type=”l”, main=”FIG.6″)
>
> #FIG.7
> acf(res, main=”FIG.7″)
>
> par(mfrow=c(2,2))
> #FIG.8-12
> plot(fitadj_trim)
Aspetto per confermare cambio pagina…
>
>
>

Far girare il precedente programma. Applicare a detrend_trim il periodogramma e trasformare in formula analitica l’oscillazione o le ascillazioni e provare a toglierla(toglierle) da medietrim (a da detrend _trim) per vedere se spariscono dal loro periodogramma i picchi rilevanti. E’ un buon metodo incrociato di testare il Periodogramma rivisitato.

16 – APPENDICE5

APPENDIX5

IL SENSO COMUNE, L’INSEGNAMENTO SCIENTIFICO ED I SAPERI PREPOSTI ALLE SCELTE – UN PRIMO APPROCCIO OPERATIVO ALL’ANALISI DI FOURIER COL SUPPORTO DEL COMPUTER del dott. Piero Pistoia

0 – LA PREMESSA

MATH_FOURIER_PREMESSA1- Piero Pistoia

BIBLIOGRAFIA DELLA PREMESSA

1 – L’ARTICOLO GUIDA

L’articolo sull’analisi di fourier su dati reali e simulati col Mathematica di Wolfram 4.2 dott. Piero Pistoia

artfouart-math in pdf

Seguirà la diretta trascrizione

2 – IL PROGRAMMA CON ESERCITAZIONI

Analisi di serie storiche reali e simulate dott. Piero Pistoia

ATTENZIONE! le linee di programma attive non sono incluse fra apici. Cambiando opportunamente le inclusioni di linee nei diversi segmenti del programma, si possono fa girare i diversi esempi, e proporne di nuovi.

A0-Esempio N.0

ANALISI DELL’ESEMPIO N° 0

Le linee attive di questo esempio sono state evidenziate

Si trascriva manualmente o con copia/incolla i seguenti scripts sulla consolle del MATHEMATICA DI WOLFRAM (vers. non superiore alla 6.0); si evidenzi e si batta shift-enter: si otterranno i risultati ed i grafici non inseriti.

"Si forniscono diversi vettori di dati sperimentali di esempio immessi 
    direttamente o tramite Table; per renderli attivi basta eliminare agli 
    estremi le virgolette.Se l'analisi diventa più complessa rispetto ad una 
ricerca di armoniche di Fourier a confronto con la serie iniziale, si può 
utilizzare il SEGMENTO DELLE REGRESSIONI (lineare e quadratica) per ottenere 
yg2 ed il SEGMENTO DELLE ARMONICHE RILEVANTI (yg3 e yg4) individuate in una 
prova precedente. Abbiamo da sostituire il nome di qualche vettore e aprire o 
chiudere (cancellando o inserendo virgolette) istruzioni nei diversi segmenti 
del programma secondo ciò che vogliamo fare. In yg1 c'è il vettore dati 
iniziale. In yg2 c'è il vettore detrendizzato. In yg3, quello delle armoniche 
rilevanti. In v, il vettore di Fourier fornito dall'analisi. Altri segmenti 
su cui intervenire: IL GRAFICO ygf dove va inserita la variabile (ygi) da 
confrontare con Fourier (v); il segmento di IMPOSIZIONE NUMERO ARMONICHE m; 
il segmento di SCELTA VARIABILI DA SOTTOPORRE A FOURIER (ygi); il segmento 
per cambiare la variabile nell'ERRORE STANDARD. In ogni esempio si accenna 
alle modifiche specifiche da apportare ai diversi segmenti";


"ESEMPIO N.0";
"Esempio illustrativo riportato alle pagine 3-4 dell'art.: imporre il numero \
di armoniche m=1 oppure 2 nel segmento relativo e confrontare il grafico ygf \
che gestisce la variabile yg1 dei dati seguenti, con quello di v (ygf1); \
controllare infine i risultati con i dati del testo";

yt=N[{103.585, 99.768, 97.968, 99.725, 101.379, 99.595, 96.376, 96.469, \
100.693, 104.443}]

"ESEMPIO N.1"
"Si sottopongono a Fourier i dati tabellati seguenti(yg1). Si confrontano yg1 \
(tramite ygf) e v di Fourier(tramite ygf1); calcolo automatico di m";
 "yt=N[Table[100+4 Sin[2 t/21 2 Pi-Pi/2]+3 Sin[4 t/21 2 Pi+0]+6 Sin[5 t/21 2 \
Pi-1.745], {t,21}]]"

"Si detrendizza yg1 seguente ottenendo yg2 (si liberino le istruzioni del \
segmento TREND), che poniamo come variabile in ygf (si inserisca nella sua \
espressione); si sottopone yg2 a Fourier (v) nel segmento "SCELTA VETTORE \
DATI"; confrontiamo ygf1 (grafico di v) e ygf; inserire variabile yg2 \
nell'espressione errore"  
"yt=N[Table[100+4 Sin[2 t/21 2 Pi-Pi/2]+3 Sin[4 t/21 2 Pi+0]+6 Sin[5 t/21 2 \
Pi-1.745]+0.5 t + (Random[]-1/2),{t,21}]]";

"ESEMPIO N.2";
"Si utilizza il vettore originale yg1 e si confronta con v di Fourier (ygf \
con ygf1), come nell'esempio N.1, prima parte; m automatico. Esempio \
interessante per controllare come Fourier legge i dati"
"yt=Table[N[Sin[2 Pi 30 t/256]+.05t+(Random[]-1/2)],{t,256}]"

"ESEMPIO N.3";
"Come l'esempio N.2. Ci insegna come Fourier <sente> i coseni"
"yt=N[Table[100+4 Cos[2 t/21 2 Pi-Pi/2]+3 Cos[4 t/21 2 Pi+0]+6 Cos[5 t/21 2 \
Pi-1.745],{t,21}]]";

"ESEMPIO N.4";
"Come il N.2. Ci assicura del funzionamento del programma"
"yt= N[Table[100+3 Sin[2 Pi 2 t/21+ Pi/2],{t,1,21}]]";
"I dati successivi sono stati campionati da Makridakis combinando l'esempio \
precedente ed un random (pag. 402, [])";
"yt={106.578,92.597,99.899,97.132,93.121,95.081,102.807,106.944,100.443,95.\
546,103.836,107.576,104.658,91.562,91.661,97.984,111.195,100.127,94.815,105.\
009,110.425}";

"ESEMPIO N.5"
"Prima parte.
Si detrendizza il vettore dati yg1, liberando, nel segmento TREND, il calcolo \
dei coefficienti B0 e B1 della retta interpolante, trovando yg2 che \
inseriremo in ygf nel segmento GRAFICO DA CONFRONTARE CON FOURIER. Calcolo \
automatico di m. Nel segmento SCELTA VETTORE PER FOURIER, poniamo yg2 in yt e \
nella formula dell'ERRORE STANDARD. Si fa girare il programma una prima volta \
e si osservano quali sono le armoniche rilevanti. Di esse si ricopiano i  \
parametri trovati (numero armonica, ampiezza, fase), con i quali  si \
tabellano le 4 armoniche rilevanti, trascrivendole nel segmento ARMONICHE \
RILEVANTI.
Seconda parte.
Nel segmento ARMONICHE RILEVANTI si tabellano le espressioni di queste 4 \
armoniche, si sommano i relativi vettori in yg3. Si liberano queste 4 \
armoniche e il loro vettore somma yg3. Si pone poi la variabile yg3 in ygf \
per confrontare yg3 con v (risultato di Fourier su yg2). Calcolo automatico \
di m. Si sceglie per Fourier la variabile yt=yg2. Nel segmento dell'ERRORE si \
pone yg3 e si rilancia il programma una seconda volta. E' un modo per \
cogliere le uniformità periodiche all'interno di dati storici"

"yt=N[{0.0330,0.0430,.0510,.0590,.0610,.0630,.053,.036,.0460,.0560,.0630,.\
0480,.0530,.0430,.0660,.053,.0820,.0600,.0800,.0760,.0560,
.0360,.0500,.053,.0560,.0580,.0610,.0630,.0650,.0680,.0815,.095,
.0790,.0630,.0690,.0740,.0800,.0765,.0730,.0695,.0660,.0930,.0830,
.0730,.0630,.0740,.0670,.06,.0860,.0800,.0730,.0670,.0890,.0640,
.0870,.079,.0700,.0650,.0600,.0630}]"

"Le successive righe sempre attive"
yg1=yt
n=Length[yt];

"SEGMENTO DELLE REGRESSIONI"

"f[x_]:=Fit[yt,{1,x,x^2},x]"
"f[x_]:=Fit[yt,{1,x},x]"

"yt1=N[Table[f[t],{t,60}]]?"
"La precedente istruzione dà problemi"

"Trovo l'ordinata all'origine e la pendenza"
"B0=f[x]/.x\[Rule]0"
"f1=f[x]/.x\[Rule]1"
"B1=f1-B0"
"B2=B0+B1 t"

"Un secondo modo di trovare B0 e B1";

"xt=Table[i, {i, 1, n}]";
"a=xt yt";
"Sxy=Apply[Plus, xt yt]";
"Sx=Apply[Plus, xt]";
"Sy=Apply[Plus, yt]";
"xq=xt^2";
"Sxq=Apply[Plus, xq]";
"yq=yt^2";
"qSx=Sx^2";
"B1=(n Sxy-Sx Sy)/(n Sxq-qSx)";
"B0=Sy/n-B1 Sx/n";
"B2=B0+B1 t";

"Tabello la retta"

"yt1=N[Table[B2,{t,n}]]"
"yt1=Flatten[yt1]"
"In yt1 ci sono i dati relativi alla retta di regressione"
"In yg2 c'è il vettore detrendizzato dei dati iniziali"
"yg2=yt-yt1"

"SEGMENTO DELLE ARMONICHE RILEVANTI"

"y4=Table[N[.004(Sin[.1333 Pi t+6.266])],{t,60}]";
"y5=Table[N[.007(Sin[.1667 Pi t+4.782])],{t,60}]";
"y8=Table[N[.004(Sin[.2667 Pi t+4.712])],{t,60}]";
"y9=Table[N[.004(Sin[.3000 Pi t+3.770])],{t,60}]";

"yg3=N[y4+y5+y8+y9]";

"In yg3 c'è il vettore dati di tutte le armoniche considerate rilevanti da \
precedente analisi. Se il programma passa da questo punto,
    ha senso misurare per es. la differenza con il vettore di tutte le \
armoniche di Fourier sui dati detrendizzati yg2";

"yg4= N[yg3+yt1]";

"In yg4 c'è il vettore di tutte le componenti considerate rilevanti compreso \
il trend. Ha senso un confronto fra i dati iniziali Yg1 o v (vettore di \
Fourier) e Yg4 "

" IL GRAFICO ygf E' DA CONFRONTARE CON QUELLO DI FOURIER ygf1"
" La variabile nel ListPlot successivo rappresenta il vettore da confrontare \
con la combinazione di armoniche di Fourier applicato ad un vettore dati. yg \
rappresenta il grafico di tale vettore"
"In ygi (i=1,2...) ci va il vettore da confrontare con v"

ygf=ListPlot[yg1,PlotJoined\[Rule]True,PlotRange\[Rule]Automatic,
    				   GridLines\[Rule]{Automatic,Automatic},
    AxesLabel\[Rule]{"Tempo","Dati \
(unità)"},PlotLabel\[Rule]FontForm["DOMINIO  DEL TEMPO",{"Times",12}]]

"CALCOLO AUTOMATICO DEL NUMERO ARMONICHE"
ny=Length[yg1]
n=ny;m=Mod[n,2]
If[m>0,  m=(n-1)/2, m=n/2-1]
"IMPOSIZIONE MANUALE NUMERO ARMONICHE"
m=1
"m=2"

"SCELTA VETTORE DATI DA SOTTOPORRE A FOURIER"
"IN yt CI SONO I DATI CHE VOGLIO ANALIZZARE CON FOURIER E L'ANALISI E' POSTA \
IN v"
"Se voglio analizzare con Fourier i dati iniziali:"
yt=yg1
"Se voglio analizzare i dati detrendizzati:"
"yt=yg2"
"Se voglio analizzare i dati relativi alle armoniche considerate rilevanti:"
"yt=yg3"
"Se voglio analizzare i dati di tutte le componenti rilevanti:"
"yt=yg4"

"VALORI DEL PARAMETRO ak="

"Calcolo gli ak con il comando Sum, sommando cioè gli n prodotti yt * la \
funzione coseno, per t=1 a n; faccio questo per ogni valore di k (da k=0 a \
n/2)tramite Table"

a1=Table [Sum[yt[[t]] Cos[2 Pi k t/n],{t,1,n}],{k,0,m}];
a=2*a1/n;

"Divido per due il primo elemento, per ottenere ao=media; Sopprimo poi il \
primo elemento"
a0=a[[1]]/2
a=Delete[a,1]
a=Chop[%]

"VALORI DEL PARAMETRO bk="

"Calcolo ora bk con la funzione seno con lo stesso procedimento di ak"
b1=Table[Sum[yt[[t]] Sin[2 Pi i t/n],{t,1,n}],{i,1,m}];
b=2 b1/n
b=Chop[%]
"Mentre ao/2 rappresenta la media, bo è sempre nullo"
b0=0

"AMPIEZZE ="

"Con ak e bk calcolo le ampiezze e le fasi dell'f(t) iniziale; Individuo il 
vettore dei numeri da mettere sulle ascisse nel dominio della frequenza 
(i/n o n/i) e con i vettori xi e yi 
costruisco la lista {xi,yi}; disegno infine i plots"
ro=Sqrt[a^2+b^2]
ro=N[Chop[%]]
ro=Flatten[ro]


Theta={}
i=1
While[i<m+1,
    f2=Abs[a[[i]]/b[[i]]];
    f2=180/Pi ArcTan[f2];
    If[b[[i]]>0 && a[[i]]>0 , Theta=N[Append[Theta,f2]]];
    If[b[[i]]<0 && a[[i]]>0, Theta=N[Append[Theta,180-f2]]];
    If[b[[i]]<0 && a[[i]]<0, Theta=N[Append[Theta,180+f2]]];If[b[[i]]>0 && a[[
    i]]<0, Theta=N[Append[Theta,360-f2]]];
    If [(a[[i]]==0 && b[[i]]==0),Theta=N[Append[Theta,0]]]; 
     If[((
    b[[i]]<0 || b[[i]]>0) && a[[i]]\[Equal]0),Theta=N[Append[Theta,0]]];
    
     If[b[[i]]\[Equal]0 && a[[i]]>0 ,Theta=N[Append[Theta,90]]];
    If[b[[i]]\[Equal]0 && a[[i]]<0, Theta=N[Append[Theta,-90+360]]]; i++];

"FASE ="

Theta=Theta

"Theta=N[ArcTan[a,b]*180/Pi]"

"RISULTATI DI FOURIER"
v=Table[a0+Sum[(a[[k]] Cos[2 Pi k t/n]+b[[k]] Sin[2Pi  k \
t/n]),{k,1,m}],{t,1,n}];

"GRAFICO RISULTATI DI FOURIER (ygf1)"
ygf1=ListPlot[v,PlotJoined\[Rule]False,GridLines\[Rule]{Automatic,Automatic},
    PlotLabel\[Rule]FontForm["GRAFICI  DI CONTROLLO",{"Times",12}]]

"CONFRONTO"
ygf2=Show[ygf,ygf1,PlotRange\[Rule]{Automatic,Automatic}]

"Calcolo l'ERRORE STANDARD DELLA STIMA"

ESS=Sqrt[Apply[Plus,(yg1-v)^2]/(n-2)]

"x=N[Table[i,{i,1,m}]]";
"c1=x";
Length[x];
Length[ro];
"For[i=1,i<m,i++,j=i*2;c=c1;yi=ro[[i]];
  c=Insert[c,yi,j];c1=c]";
"d1=Partition[c,2]";
Needs["Graphics`Graphics`"]
BarChart[ro]
ListPlot[ro, PlotJoined\[Rule]True,PlotRange\[Rule]All, 
  GridLines\[Rule]{Automatic,Automatic},AxesOrigin\[Rule]{0,
          0},AxesLabel\[Rule]{"Cicli in n dati", "Ampiezza \
"},PlotLabel\[Rule]FontForm["DOMINIO  DELLA FREQUENZA",{"Times",12}]]
"c1=x";
"For[i=1, i<m,i++,j=i*2;c=c1;yi=Theta[[i]];
  c=Insert[c,yi,j];c1=c]";
"d2=Partition[c,2]";
ListPlot[Theta, PlotJoined\[Rule]True,PlotRange\[Rule]All, \
GridLines\[Rule]{Automatic,Automatic},AxesOrigin\[Rule]{0,0},
  AxesLabel\[Rule]{"Frequenza","Fase"}]

———————————————————————————–

A1-Esempio N.1

————————————————————————

A2-Esempio N.2

RISULTATI ESEMPIO 2

A5-Esempio N.5

Serie detrendizzata delle concentrazioni As

ANALISI DEI DATI REALI DELL’ESEMPIO N° 5

L’IDEA E’ QUESTA:

– SUI SESSANTA DATI DELLA CONCENTRAZIONE ARSENICO (yt, GRAF. N.1) IN ALCUNE SORGENTI DELLA CARLINA (PROV. SIENA), SI FA UNA REGRESSIONE LINEARE ED I SUOI 60 VALORI PREDETTI SI SOTTRAGGONO DA yt, OTTENENDO LA SERIE DETRENDIZZATA.

– QUEST’ULTIMA SI SOTTOPONE AL PERIODOGRAMMA CHE, IN USCITA, PERMETTE DI CALCOLARE LE SUE COMPONENTI ARMONICHE.

– SOMMANDO LE COMPONENTI ARMONICHE RILEVANTI PIU’ I VALORI DEL TREND E SOTTRAENDO TALE SOMMA DALLA SERIE ORIGINALE yt, SI OTTERRA’ LA “STIMA DELL’ERRORE STANDARD” CHE DA’ UN’IDEA DELLA BONTA’ DEL PROCESSO.

Si trascriva manualmente i seguenti scripts sulla consolle del MATHEMATICA DI WOLFRAM (vers. non superiore alla 6.0); si evidenzi e si batta shift-enter: si otterranno i risultati e grafici riportati alla fine di questo programma (si noti in particolare il grafico ampiezza-numero armoniche eseguito sulla serie detrendizzata, dove è evidente il picco all’armonica n°5)

——————————————————————–

RISULTATI DEL PROGRAMMA ESEMPIO N.5 (conc. As detrend)

A4-Esempio N.4

ANALISI DELL’ESEMPIO N° 4 CON RISULTATI E GRAFICI (DATI SIMULATI)

A6-Esempio N.6

Oscillazione mensile ozono a Montecerboli (Pomarance,Pi); 2007-2011

RISULTATI GRAFICI OZONO

———————————————————————————-

ESEMPIO N° 5 CHE USA LE ARMONICHE RILEVANTI MESSE IN FORMULA IN UNA PRE-PROVA

FOUART-articolo-Piero Pistoia-in pdf

—————————————

four_art1 da correggere

fuor_art19 da correggere

piero-pistoia-curriculumok-1-35 Download

ALCUNE LEZIONI DI FISICA RELATIVISTICA, a più voci; dott. prof. Rosa-Clot, dott. prof. F. de Michele, dott. prof. G. Cellai, dott. P. Pistoia; post aperto

Immagine | Posted on settembre 13, 2013 by pierfrancesco1952

Testo rivisitato da “il Sillabario”, n. 2 1996

demic (2)

demic2

Testo rivisitato da ‘Il Sillabario’, n. 3 1996

demic3

Testo rivisitato da ‘Il Sillabario’, n. 4 1997

figura22

Testo rivisitato da ‘Il Sillabario’, n. 1 1998

figura24

figura25

IL PARADOSSO DEI GEMELLI?

Dott. Prof. Marco Rosa-Clot

Fisico Teorico, Università di Firenze

“Sono convinto che i filosofi hanno sempre avuto un effetto dannoso sul progresso del pensiero scientifico poiché hanno sottratto molti concetti fondamentali al dominio dell’empirismo, nel quale si trovavano sotto il nostro controllo, e li hanno portati alle intangibili altezze dell’“a priori “.

Questa frase polemica e di sapore vagamente oscurantista apre il famoso libro di Einstein “Il significato della relatività” in cui viene esposta in modo conciso e compiuto, la teoria della relatività galileiana, speciale e generale (il lettore non si faccia illusioni: il libro è un capolavoro di chiarezza ma richiede approfondite conoscenze di geometria differenziale ed è tutt’altro che accessibile ai non specialisti).

Sorvoliamo sulla polemica, evitiamo di richiamare l’importanza per la storia del pensiero umano della speculazione filosofica, e umilmente seguiamo la lezione empirista.

Saliamo su un aereo, controlliamo l’orologio. Partiamo da Roma e facciamo rotta equatoriale verso Tokyo. Io passando da Bombay e voi da NewYork. A Tokyo prendiamo un caffè e poi continuiamo il nostro viaggio (ognuno nella sua direzione) per poi ritrovarci a Roma allo stesso punto a circa due giorni dalla partenza.

Controlliamo gli orologi: il mio orologio (ho viaggiato verso est) segna un tempo maggiore del vostro. Vi posso assicurare che i due orologi sono identici, che funzionano benissimo, non c’è trucco. Se partendo avevamo la stessa età ora voi siete in realtà un po’ più giovani di me. Mica di tanto si capisce; controllando bene si tratta di soli 300 nanosecondi, cioè 0,3 milionesimi di secondo; ma siete più giovani! Questo è il punto.

Quello che ho descritto è in effetti l’esperimento di Hafele e Keating (due fisici americani) del 1971. I due aerei scelti per l’esperimento hanno volato per circa 50 ore e i due orologi erano due orologi atomici identici in grado di apprezzare il miliardesimo di secondo (il nanosecondo).

La teoria della relatività prevedeva in questo caso una differenza di tempi di 315 ±30 nanosecondi (miliardesimi di secondo), il risultato sperimentale trovato fu di 332±12 ns. Un successo straordinario dell’analisi teorica di Einstein di più di mezzo secolo prima. Un risultato giudicato dai contemporanei prima manifestamente falso e poi paradossale: il paradosso dei due gemelli.

All’epoca fu infatti proposto un “gedenken experiment” (un esperimento pensato): uno dei due gemelli intraprende un viaggio spaziale a velocità prossima a quella della luce e quando ritorna trova il fratello molto più vecchio di lui: il tempo e passato in modo diverso per i due soggetti.

Hafele e Keating hanno realizzato questo esperimento utilizzando i mezzi di trasporto disponibili e migliorando enormemente il sistema di misura del tempo: non si guardano i capelli bianchi di un uomo ma si contano le oscillazioni degli atomi di cesio di un orologio atomico.

Ma perché parlare di paradosso?

E’ paradossale che una trottola in rapida rotazione non cada e si mantenga in equilibrio sulla sua punta? Dipende dai punti di vista ma soprattutto dall’abitudine. Fin da bambini abbiamo visto trottole girare e ora ci sembra del tutto naturale che ciò avvenga. Inoltre le leggi della meccanica del corpo rigido spiegano benissimo questo fenomeno in tutti i suoi dettagli.

E’ paradossale che un aereo voli? Forse, ma a partire dagli studi di Leonardo e dalle sue osservazioni sul volo degli uccelli lo è un po’ meno, e oggi è certamente considerato un fatto quanto meno ovvio; anzi è paradossale che un aereo cada.

Continuiamo a seguire umilmente la lezione empirista e poniamoci una prima domanda: cosa è il tempo? (dal punto di vista fisico si intende, non soggettivo o meteorologico od altro).

La fisica considera il tempo in modo empirico come una grandezza continua, misurabile con orologi, e che scorre in una sola direzione.

L’individuazione di un evento avviene assegnandone le coordinate spaziali e l’istante temporale in cui si verifica. La principale differenza tra posizione e tempo sta nella possibilità di muoversi lungo le coordinate in ogni direzione mentre il tempo è per sua natura unico e percorribile solo in un senso.

La fisica assegna anche leggi di trasformazione delle coordinate che sono deducibili da osservazioni sperimentali. Per esempio l’osservazione empirica comune ci insegna che la posizione di un viaggiatore su un treno in movimento con velocità v rispetto a un amico fermo in stazione sono date da x’ = x_o + vt dove x_o è la sua posizione all’istante t=0 (trasformazione della relatività galileiana), mentre il tempo per i due amici è lo stesso: t’ = t.

La fisica relativistica, a partire dall’osservazione che la velocità della luce nel vuoto è invariante a prescindere dal sistema di riferimento in cui viene misurata, arriva ad altre relazioni: le trasformazioni di Lorentz.

Certo è paradossale affermare che la velocità della luce è la stessa sia che il raggio luminoso parta da un treno in corsa che dall’osservatore fermo. Per la bottiglia di gazzosa lanciata dal finestrino non è certo la stessa cosa: in un caso il signore in stazione la lascia cadere correttamente nel cestino dei rifiuti, nell’altro il passeggero sul treno in corsa la lascia cadere dal finestrino e il risultato può essere disastroso.

Tuttavia i fotoni non sono bottiglie di gazzosa e potremmo dire che sarebbe piuttosto paradossale trattarli alla stessa stregua.

Allora seguiamo ancora la lezione dell’empirismo ed accettiamo che c è costante. Paradossale ma vero, quindi non paradossale. Se prendiamo la parola nel suo etimo (al di là dell’opinione) c = costante in ogni sistema di riferimento è una realtà fisica e quando ci si abitua a questo, per definizione non è più paradossale.

L’implicazione delle trasformazioni di Lorentz sull’intervallo temporale sono semplici:

e ricordando che dx = vdt

che per velocità v piccole rispetto a c si può scrivere

Questa formuletta merita di essere illustrata in un grafico.

Supponiamo di studiare due diversi percorsi nello spazio tempo (vedi fig. 1). In un primo caso (cammino a) il soggetto a sta fermo nella posizione x=x_o

e si trova dopo un tempo Dt nella stessa posizione senza mai muoversi. Nel secondo caso (cammino b) il soggetto b si allontana dalla posizione originaria per poi tornarci. Nel far questo il suo tempo cambia secondo la legge:

enunciata sopra e quindi quando torna al punto B il suo tempo risulta minore! la linea retta tra due punti nello spazio tempo della relatività risulta essere la più lunga possibile rispetto a qualsiasi altra congiungente!

Figura 1: Rappresentazione schematica del percorso dei due gemelli che vanno dal punto A (di coordinata xo) al punto B (stessa coordinata spaziale) lungo due diversi percorsi. Percorso a : il gemello 1 sta fermo e lascia passare il tempo da t_o a t₁. Percorso b: il gemello 2 si allontana da x_o per poi ritornare a x_o e ritrovarsi con il gemello 1 al punto B all’istante t₁.

Paradossale! ma vero e inoltre osservato (quindi non paradossale).

Si noti che il tempo proprio dei due osservatori non viene alterato; gli orologi atomici non rallentano o accelerano e (ciascuno nel suo sistema) soddisfano immutati le stesse leggi della fisica atomica e dell’elettromagnetismo. Cambia la distanza di tempo relativa. Inizialmente nulla, essa aumenta progressivamente fino a diventare 330 ns alla fine del viaggio.

Per comprendere meglio il fenomeno serviamoci di una analogia: due esploratori all’equatore si trovano alla distanza di 100 Km e si mettono entrambi incammino verso Nord (si noti muovendosi “parallelamente” e su un percorso rettilineo perpendicolare all’equatore stesso). Dopo 100 Km misurano la loro distanza e scoprono che si e’ ridotta di 31 cm. Se continuassero nel loro percorso vedrebbero la loro distanza ridursi ancora sempre più rapidamente fino a diventare zero nel punto di incontro al polo.

La risposta a questa osservazione può essere un sorrisetto di sufficienza: grazie! Sappiamo tutti che la geometria della sfera e’ tale che due meridiani si avvicinano e poi si incontrano (due archi di cerchio massimo, cioè due parallele). Abbiamo solo scoperto che le leggi di trasformazione delle coordinate non sono quelle del piano euclideo.

Torniamo all’esperimento di Hafele e Keating. In un caso la velocità dell’aereo si somma a quella di rotazione della terra (viaggio orario verso ovest) nell’altro caso si sottrae. e da cui:

Δτ₁ = dt [1+(v_T+v_a)²/c²]^1/2; Δτ₁=Δ t v_Tv_a/(2c²)] e

Δτ₂ = dt [1 + (v_{T –}v_a)²/(2c²)]; Δτ₁ – Δτ₂ =4Δ t v_Tv_a/(2c²)

Ma v_T= ωR dove ω è a velocità di rotazione terrestre (ω = 2π/ N_s dove N_s e’ il numero di secondi in un giorno: N_s = 8600 sece R è il raggio equatoriale e Δtv_a=2πR . Quindi Δτ₁ – Δτ₂ =4πωR²/c², circa uguale a 400ns.

Quindi Utilizzando il percorso effettivamente fatto dagli aerei (non seguivano orbite esattamente equatoriali) si trova il risultato citato sopra.

Se queste poche righe hanno lasciato pensare che la frase di Einstein sui filosofi sia da me condivisa chiedo venia al paziente lettore. Spero invece che il discorso sull’empirismo sia accettato nella sua globalità.

Certo la relatività non ci mette a disposizione un metodo per ringiovanire (il tempo scandito dagli orologi atomici scorre inesorabile nei due sistemi di riferimento) ma sicuramente possiamo abbreviare i viaggi spaziali.

Da questo punto di vista l’ignoranza della relatività da parte dell’equipaggio della Enterprise è sconfortante. Questa benedetta astronave si ostina a viaggiare a velocità superiore a quella della luce e ad usare una fisica non relativistica. Orbene, la galassia ha un diametro di 100mila anni luce. Che me ne faccio di una astronave che viaggia 100 volte più veloce della luce e ci mette 1000 anni a raggiungere i Klingoni in capo alla galassia.

Ben altra lezione ci viene dal mondo reale. Arrivano regolarmente sulla terra raggi cosmici con energia di milioni di TeV (tera electronvolt). Un protone con una energia di un milione di TeV (10¹⁸ ev) ha un velocità molto vicina a quella della luce (0.9999999999999999995*c : ci sono 18 cifre 9 dopo lo zero). Ma quello che più interessa è che il rapporto tra il suo tempo e quello di un osservatore fermo è dato da:

che è uguale dt/10⁹.

Quindi in poco più di mezz’ora (del suo tempo proprio) il protone attraversa la galassia e in 10 anni l’intero universo. Povero Star Trek! E questa è fisica!

(Marco Rosa-Clot, fisico Teorico)

(Rivisitato da Il Sillabario, n.4, 1997, XI)

PER VEDERE IL CURRICULUM DI MARCO ROSA-CLOT CLICCARE SU:

mrcsh-it-1

______________________________

Vedere anche “Un possibile racconto sulla relazione fra massa ed energia” di Piero Pistoia; nell’intenzione, a taglio più didattico argomentativo.

PROLOGO ALL’ARTICOLO scritto da Piero Pistoia

In via di sviluppo; rivisitato e corretto da Il Sillabario n. 4 1995; da esso in particolare riprese le immagini.

Alcune argomentazioni su dubbi!

L’ARGOMENTAZIONE SVILUPPATA IN QUESTO RACCONTO CERCA DI SEMPLIFICARE IL PERCORSO CONCETTUALE SEGUITO NEL TESTO “PHYSICS FOR THE INQUIRING MIND” BY ERIC M. ROGERS, Princerton University press, Cap. 31. Tale testo al tempo fece epoca. Il capitolo 31 sulla Relatività fu poi tradotto anche in italiano per il “The Project Physics Course” della Zanichelli, Unità 4 e Unità 5, 1982. Questa traduzione fu inserita nella Prima Lettura, pagg. 5/114-5/141.

AFFERMAZIONE DI ROGERS NEL CUORE DELL’ARGOMENTAZIONE

“…Then ε, watching ε’ at work, sees that ε’ uses a clock that runs slowly (but they agree on normal meter sticks in the y-directions). So ε sees that when ε’ said he misured 3 meters travel in 1 sec, it was ‘really’ 3 meters in more-than 1-second as ε would misure it by his clock…” by Rogers pag. 486

___________________________RIQUADRO_______________________

CAPITOLI

2 – NOZIONI NECESSARIE DI FISICA ELEMENTARE

3 – NOZIONI NECESSARIE DI RELATIVITA’ RISTRETTA

4 – RELAZIONE FRA MASSA ‘A RIPOSO’ E MASSA IN MOVIMENTO: UN ESPERIMENTO “PENSATO” ALLA GALILEO

5 – LA RELAZIONE FRA MASSA ED ENERGIA

6 – NOTE

7 – IL DUBBIO

____________________________________________________________

CLICCANDO SOPRA GLI SCRITTI POCO LEGGIBILI SI INGRANDISCONO

CENNI DI NOZIONI NECESSARIE DI RELATIVITA’ RISTRETTA

I Postulati della Relatività Ristretta di Einstein affermano 1) Tutte le leggi fisiche sono le stesse in tutti i sistemi di riferimento inerziali (“spazi” che traslano reciprocamente di moto rettilineo uniforme). 2) la velocità della luce (nel vuoto) è la stessa per ogni osservatore in un sistema di riferimento inerziale, qualunque sia il moto relativo fra la sorgente luminosa e l’osservatore. Su questi postulati si “costruiscono”, senza grandi difficoltà matematiche (a parte qualche sottigliezza concettuale), le così dette Trasformazioni di Lorentz (quelle di Galileo riguardavano lo stesso argomento senza considerare il 2° postulato), che rappresentano le relazioni fra coordinate di uno stesso evento “lette” da due osservatori situati in due “zone di spazio” che si muovono relativamente di moto rettilineo uniforme con velocità V. Senza entrare nel merito, queste trasformazioni permettono di affermare fra l’altro che a) Ogni osservatore di un sistema inerziale pensa di essere in quiete e vede gli oggetti sull’altro sistema scorciarsi nella direzione del moto di un fattore 1/R=√(1-V²/c² ) se R=(1-V²/c²)^-1/2. R è anche circa uguale a: 1+1/2*V²/c² . Se V è minore di c (oggetti-massa), R è maggiore di 1; in buona approssimazione è 1 se V è molto minore di c (V<<c); √(1-V²/c² ) < 1. b) Ogni osservatore che pensa di essere in quiete (es., Oa), vede rallentare l’orologio dell’altro sistema (Ob) ancora di un fattore R. Per Oa rallentano anche le vibrazioni degli atomi e quindi anche gli orologi atomici, il battito del cuore, il metabolismo degli organismi viventi, che probabilmente condiziona tutto il processo vitale (il ciclo vitale degli organismi aumenta insieme alla speranza di vita; si invecchia più lentamente [ha senso qui la relazione Δtb = Δta * √(1-V²/c² )]. Ad ogni intervallo fra ticks successivi corrispondente ad un secondo letto nell’orologio dell’osservatore che pensa di essere in quiete, corrisponde più di un secondo nell’orologio di Ob (per ogni secondo → 1 sec*R; 3 sec in Oa, 3*R sec in Ob, sempre registrati da Oa ). In termini di pendolo, se i due osservatori hanno un pendolo che batte il secondo (oscillazione completa in un secondo misurata da ogni osservatore all’interno del proprio sistema), se Oa (in quiete) guarda il pendolo di Ob, vede che, quando il suo pendolo termina l’oscillazione completa (1 sec), l’altro (OB) ha ancora da terminarla. Che cosa accade ad R se V si avvicina a c? E se V supera c? E delle misure delle dimensioni degli oggetti ? (l=lo/R, vedere (i) e (ii) nella figura sotto) e del tempo? (t=to*R? vedere (iii) nella figura sotto o t=to/R?); ancora da approfondire!.

Come cambiano le misure predette dalla relatività

L’immagine sopra riportata con scritti in inglese si trova nel cap. 31 pag. 485 del testo “Physics for inquiring mind” di Eric M. Rogers; in italiano si trova invece nelle ‘Letture’ pag, 5/127 del testo “The project Physics Course, Unita’ 5 e Unita’ 6” Zanichelli editore e noi l’abbiamo presa in prestito.

La Figura sotto rappresenta invece un esperimento costruito nella mente, di fatto scarsamente praticabile, ma che pensiamo possa facilitare l’apprendimento del concetto (ipotesi: le due masse rimarranno uguali? Certamente! almeno il tipo di atomi e il loro numero rimarranno gli stessi). Centinaia sono stati gli scritti sulla relatività di Einstein dopo la sua pubblicazione all’inizio del XX° secolo e altrettanti verranno pubblicati nel corso del nuovo secolo, con i loro obiettivi, i loro percorsi rilevanti, i loro stratagemmi, le loro ‘fisiologie’ intendo. Nel nostro caso ci sono due osservatori in due “spazi” paralleli, che si muovono relativamente in verso opposto di moto rettilineo uniforme con velocità relativa V. Ciascun osservatore possiede un oggetto-massa identico (stesso contenuto di materia) posto in quiete su un piano privo di attrito. Si appoggi ai due oggetti (chi e come non si sa!) un sistema ‘molla compressa-corda’ privo di massa nel momento di incontro, quando i due spazi si trovano di fronte lungo Y e la molla termina l’azione proprio quando gli orologi dei due sistemi segnano zero secondi (sic!). Per la sincronizzazione degli orologi, posti ai nodi di strutture spaziali ‘a tubi innocenti’ ed altro, si rimanda all’articolo di Giorgio Cellai in questo blog. Sono uguali e opposti gli impulsi nei due sistemi e, per come è stata la spinta, per ogni osservatore all’interno del proprio spazio, appena caduta la molla, i due oggetti si muovono lungo la direzione dell’asse y in versi opposti di moto uniforme con uguali quantità di moto. Per la conservazione della quantità di moto vettoriale infatti, sia il vettore M*Va sia il vettore di verso opposto M*Vb continueranno a ‘guardare’ nella direzione dell’asse Y. Per la fisica classica le due velocità dovranno essere le stesse! Ma misuriamole tenendo conto delle trasformazioni relativistiche accennate! Da notare che, se, per es., l’osservatore A pensa di essere fermo, vede muovere l’oggetto in B lungo la diagonale di lati V e vb (!), il metro lungo X si contrae, ma noi siamo interessati solo al movimento lungo y. Se due masse Mb e Ma interagiscono sotto lo stesso impulso, in un sistema isolato, come già accennato, la Quantità di Moto totale è costante nel tempo. Tenendo conto delle condizioni iniziali (per t=0, vb1=va1=0) otteniamo Ma*va = Mb*vb e se, per l’osservatore A per qualche ragione, vb=va/R, vb diminuisce di R, per cui Mb=Ma*va/vb aumenta di R. E viceversa per l’osservatore B. Se partiamo con due masse uguali , Mb=Ma, otteniamo che Mb diventa maggiore di Ma a causa del movimento (ancora da rifletterci)._____________________________RIQUADRO___________________

Per qualsiasi valore di V anche per V/c<<1:

M-Mo = Mo*R – Mo dove R=1+1/2*V^2/c^2 ; se

M-Mo = Mo*(R-1) allora M-Mo = 1/2 * Mo*V^2/c^2 =Er/c^2

ΔM =Er/c^2

Se V<< c, fornendo energia cinetica (tramite lavoro di una forza , urto…) o energia di qualsiasi altro tipo (es., calore), la sua massa , in conseguenza di ciò, aumenta di Er/c^2 e viceversa. (Da chiarire ulteriormente)

Attenzione: è la V, velocità relativa dei due spazi, che fa rallentare gli orologi, non le velocità delle due masse, indicate con Va e Vb ovvero va e vb o altro! R=1+1/2*V^2/c^2

__________________________________________________________

Piero Pistoia

N.B. – I DUBBI SU ALCUNI PASSAGGI CONCETTUALI SONO STATI DISCUSSI CON L’ING. RODOLFO MARCONCINI E COMUNICATI ANCHE AL PROF. GIORGIO CELLAI.

IL DUBBIO: Dai principi della Teoria è possibile derivare logicamente in ogni caso la seguene relazione?

Δtb = Δta / √(1-V²/c² ) –> Δtb aumenta in questo modo in ogni condizione?

FORSE! LA SOLUZIONE DEL

DUBBIO_ rel1

ancora in pdf

LORENTZ_RELATIVITA’OK1

CURRICULUM DI PIERO PISTOIA:

cliccare su:

piero-pistoia-curriculumok (#)

LA POESIA di Guido Gozzano ed altro, Commenti dei docenti di Lisa Fedeli, Nara Pistolesi, Piero Pistoia, Gabriella Scarciglia, Francesco Gheradini; post aperto a più voci; da commentare la poesia aggiunta”Cocotte”

Immagine | Posted on settembre 11, 2013 by pierfrancesco1952

Testi rivisitati da ‘Il Sillabario’, n. 2 1999

Da commentare la poesia “Cocotte” riportata nel link seguente:

COCOTTE – E’ DA QUESTA POESIA DI G. GOZZANO CHE NASCE LA MITICA FRASE “NON AMO CHE LE ROSE CHE NON COLSI” _ IL MONDO DI ORSOSOGNANTE

Sono inseriti due intermezzi: “L’assenza di fondamenti” di Varela e l'<<anyThing goes>> di Feyerabend.

Segue una pittura di Gabriella Scarciglia:

goz2

SE VUOI LEGGERE PIU’ CHIARAMENTE IL TESTO DELLA POESIA E IL BREVE PENSIERO DI VARELA (‘Assenza di fondamenti’) IN PDF, CLICCA SU:

gozzano0002

::::::::::::::::::::::::::::::::::::::::::::::::::

COMMENTO DI LISA FEDELI

:::::::::::::::::::::::::::::::::::::::::::::::

COMMENTO DI PIERO PISTOIA – SCARCIGLIA

Curriculum di piero pistoia:

PIERO PISTOIA CURRICULUMOK

ESPERIMENTO DI INTERPRETAZIONE DI UNA POESIA

PER VEDERE IL COMMENTO IN PDF DI PISTOIA-SCARCIGLIA IN MODO PIU’ CHIARO, CLICCARE SU:

gozzano_pistoia

altrimenti:

goz5

N.B. – I tre riferimenti nel precedente commento rimandano al Sillabario cartaceo da cui sono stati enucleati, rivisitati e trasferiti in questo blog, cercando, per es., con la le parole “Enantiodromia” e “Fabbri”.

:::::::::::::::::::::::::::::::::::::::::::::::

COMMENTO GHERARDINI

PER VEDERE IL COMMENTO DI GHERARDINI e il breve ‘anything goes’ di Feyerabend in pdf, in modo più chiaro, CLICCARE SU:

gozzano_gherardini

gozza4

:::::::::::::::::::::::::::::::::::::::::::::::::::

Se vuoi leggere il commento della prof.ssa Nara Pistolesi clicca qui sotto:

GUIDO_GOZZANO_COMMENTO_NARA_PISTOLESI_prima_versione_in_pdf

GOZZANO_La_via_del rifugio_N_PISTOLESI_seconda_versione_in_doc

GOZZANO_La_via_del rifugio_N_PISTOLESI_seconda_versione_in_pdf

LA POESIA “TRAVERSANDO LA MAREMMA TOSCANA “, di Giosuè Carducci; commento a più voci (“pittura di Gabriella Scarciglia”)

Immagine | Posted on settembre 11, 2013 by pierfrancesco1952

Testi rivisitati da ‘Il Sillabario’, n. 3 1997

ESISTE UN METODO DI INVESTIGAZIONE ALTERNATIVO ALLA SCIENZA? es. il sacro, il magico, l’arte, medicina alternativa…, a cura del dott. P. Pistoia; post aperto ad altri svariati interventi

Immagine | Posted on settembre 5, 2013 by pierfrancesco1952

Curriculum di piero pistoia :

piero-pistoia-curriculumok (#)

NOTA BENE

Per comprendere un “oggetto” complesso multidimensionale è necessario “osservarlo” da diversi punti di vista indipendenti (uno dei criteri di questo blog). Così l’oggetto culturale “Religione“, a più dimensioni, verrà ‘letto’ in questo blog, da scritti più o meno ortodossi e difformi. Per trovare questi scritti, cercare con il tag, per es., “Religione”.

MOLTI DEGLI SCRITTI E LE FOTO DI QUESTO POST SONO STATI TRASFERITI DALL’EX-INSERTO CARTACEO, IL SILLABARIO, DELLA COMUNITA’ DI POMARANCE.

Ragione, senso dell’arte e del sacro, di Piero Pistoia. Intermezzo: poesia “La conchiglia” di Fidanzi e pittura di Cangio “Galli”
Ricerca di un metodo di conoscenza alternativo di Piero Pistoia
Valore cognitivo del pensiero magico di Cristina Ghilli
Aspetti antropologici del pensiero magico di Cristina Ghilli
I riflessi della cultura magica nel mondo occidentale moderno di Cristina Ghilli. Intermezzo: il miracolo di don Serafino Falvo, il carismatico,
Il miracolo di don Marco Fabbri, il teologo.
Il miracolo di Antonio Zani
Cose dell’Universo, dott. Piero Pistoia

Come ultimo intervento presentiamo anche il pensiero dei ‘Testimoni di Geova’ riportato sulla Torre di Guardia’, 1° Ottobre 2010, dove si argomenta con precisi riferimenti ad un Testo Sacro, la Bibbia (il link è ancora da attivare)

Poesia e scienza
scansione0006

Ragione, senso dell’arte e del sacro

Testo rivisitato da il ‘Sillabario’ n. 3 1996
figura4

Ricerca di un metodo di conoscenza alternativo

Testo rivisitato da il ‘Sillabario’ n. 2 1997

alternativ

pistoching0003

Valore cognitivo del pensiero magico

Testo rivisitato da il ‘Sillabario’ n. 1 1995

ghilli

Aspetti antropologici del pensiero magico

Testo rivisitato da il ‘Sillabario’ n. 4 1996; 1-2 1997

ghil2

PARTE SECONDA

cristighil0002

PARTE TERZA

crist0002

I riflessi della cultura magica

Testo rivisitato da il ‘Sillabario’ n. 1 1996
figura35

PARTE SECONDA

Testo rivisitato da il ‘Sillabario’ n. 2 1996

cristo0001

crist0001

Il miracolo di M- Fabbri

Testo rivisitato da il ‘Sillabario’ n. 1-2 1996
fab

fab1

Il miracolo di A. Zani

Testo rivisitato da il ‘Sillabario’ n. 2-3 1999

zani

zani1

zani2

zani3

Cose dell’universo

Testo rivisitato da il ‘Sillabario’ n. 2 1999

gozza1

Direttore culturale del vecchio SILLABARIO

RIPORTIAMO, INFINE, COME UNA DELLE ‘DIMENSIONI’ CULTURALI DEL NOSTRO POST ANCHE IL PENSIERO DEI ‘TESTIMONI DI GEOVA’

Cliccare su

PREGHIERA E MIRACOLO

	pierfrancesco1952 su ALCUNI SCRITTI DEL POETA_SCRIT…
	abdensarly su ALCUNI SCRITTI DEL POETA_SCRIT…
	abdensarly su ALCUNI SCRITTI DEL POETA_SCRIT…
	paolo fidanzi su DAL FILM “SPARTACUS” LA POESIA…
	acutamente su UNA ‘CALDA’ POESIA…