Archivi tag: dott. prof. Giorgio Cellai
SCALA MUSICALE “UNIVERSALE”; dott. prof. Giorgio Cellai
Il seguente articolo rappresenta il quarto articolo dopo Induzione Matematica, Successioni sui numeri reali, Progressioni sui reali, costituenti nell’insieme un modulo di insegnamento. Si può leggere in successione l’intero modulo in questo blog cercando BREVI LEZIONI
Per leggere questo scritto in pdf, cliccare su:
PARLEREMO DI UN ESPERIMENTO DIDATTICO PER CONTROLLARE SE OGNI OGGETTO DELL’UNIVERSO POSSA AVERE LA STESSA MASSA GRAVITAZIONALE ED INERZIALE: rivisitazione, secondo il nostro intendimento, dell’esperimento condotto dall’accademico prof. Placido D’Agostino dell’università di Messina; a cura del dott. prof. Giorgio Cellai e dott. Piero Pistoia, ambedue di ruolo ordinario in fisica.
Articolo in via di costruzione….da modificare ampliare e correggere.
CURRICULUM DI PIERO PISTOIA :
piero-pistoia-curriculumok (#)
Per leggere l’articolo in pdf cliccare sul link:
Oppure continuare a leggerlo di seguito.
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
PROLOGO
capire non sanno
come.
discorde in sè, si accordi…
corda d’arco e di lira,
che agli opposti si tende
in armonia.
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
PREMESSA PER IL CALCOLO DELLA MASSA INERZIALE
Il concetto di massa inerziale ‘gioca’ sui palcoscenici dove si sprigionano cambiamenti di velocità fra oggetti, in particolare in teatri dove avvengono urti, quasi che gli oggetti dell’Universo posseggano intrinseche proprietà di opporsi a questi cambiamenti. Per altri ricercatori (Mach, Einstein) il concetto di inerzia acquista significati diversi. Per noi, che vogliamo studiare e quantificare questo concetto, sarà invece necessario guardare in questi ambiti, dove masse interagenti scambiano fra loro energie e velocità, onde fare le nostre osservazioni utilizzando opportuni linguaggi. Utilizzeremo così processi che coinvolgono variazioni di quantità di moto e di energie cinetiche.
Interessante è rivisitare, usando la mente, come in qualche modo tentava di fare Semplicio nel contraddittorio con i colleghi di dialogo (Galileo e Sagredo ovvero Salviati), precisandone alcuni aspetti, l’esperimento proposto dal prof. Placido D’Agostino, dell’Istituto di Fisica dell’Università di Messina, pubblicato nella rivista “La fisica nella scuola”, ottobre-dicembre del lontano 1982, usando una apparecchiatura di maggiore precisione (rotaia a cuscinetto d’aria), rispetto a quelle, al tempo, secondo noi, statisticamente usate più spesso, in dotazione dei laboratori della Scuola Superiore, con utilizzo anche di un cronometro che aveva al max la precisione solo di un centesimo di secondo, dotato di interruttori a contatto spostabili lungo la rotaia.
Ad uno degli scriventi, cercando di riordinare alla meglio studio, tappezzato, pavimento e pareti, di miriadi di libri e riviste aperti, migliaia di fotocopie in parte spillate o incollate in enormi blocchi, fogli di appunti e di aforismi (fra cui spiccava “L’ORDINE E’ LA VIRTU’ DEI MEDIOCRI”)…, gli è capitato in mano una rivistina, aperta alla pagina 143, dove in alto a destra appariva la scritta DIDATTICA ed a sinistra PLACIDO D’AGOSTINO Istituto di Fisica dell’Università Messina” e sotto un titolo interessante in neretto “L’urto elastico usato come verifica dell’uguaglianza fra massa gravitazionale e massa inerzia; nella pagina successiva appariva in alto in caratteri piccoli il titolo ed il numero della rivista “La fisica nella Scuola,XV, 4” e a destra una tabella con valori di misure di grandezze con errori assoluti certamente piccoli: nulli addirittura sui rapporti fra masse gravitazionali, circa 1 millimetro sugli intervalli di spazio e sugli intervalli corrispondenti di tempo errori fino al millesimo di secondo, da destare meraviglia a fronte dei ricordi che aveva relativi a misure fatte quando era docente di Fisica e Laboratorio al biennio dell’ITI, un Istituto Tecnico di una provincia lontana da una città media.
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Per leggere direttamente l’articolo dell’accademico P. D’Agostino in pdf, cliccare sul link:
(E’ consentita la riproduzione fotostatica delle pagine della rivista)
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
In particolare, in una prima veloce lettura, ci ha colpito il risultato finale rappresentato dalla media delle differenze fra i rapporti fra massa gravitazione e quelli fra massa inerziale, infatti per questa media di tali differenze riportata era 5.512*10^(-4), con errore assoluto sulla quarta cifra significativa, errore relativo (0,001/5.512); percentuale 0.018% ! Su tale risultato l’autore afferma : <<Data la natura prettamente didattica e dimostrativa di questa esperienza, i risultati ottenuti si ritengono soddisfacenti>>. Comunque se ci farà voglia proveremo a ricalcolarlo.
Chi vuol vedere come si calcola direttamente dalla scrittura di una misura il suo errore percentuale, cliccare sul link: dagostino0001
Il dott. prof. Giorgio Cellai, docente di ruolo in fisica al Liceo Scientifico, contribuisce con una argomentazione critica sul calcolo degli errori nell’articolo in oggetto, e sulla loro interpretazione.
Vedere di seguito il link:
Interessante confrontare l’errore direttamente “ricavato dalla scrittura” della misura della media delle differenze fra rapporti delle due masse, con l’argomentazione accennata da Cellai su tale valore.
ALCUNI PASSAGGI IMPLICITI DA RENDERE TRASPARENTI AL LETTORE MEDIO
Non esiste nell’articolo alcuna descrizione né disegno della apparecchiatura, né come si ponga il cronometro digitale ad alta precisione con relativi contatti mobili per on/stop; ci si limita a dire, almeno così ho capito, che si tratta di una rotaia ad aria per rendere minimi gli attriti, che saranno usate per le varie prove, come si ricava dalla tabella, 10 coppie di oggetti già tarati a corredo dell’apparecchiatura, di massa m1 e m2 variabile, i cui valori formino rapporti che cambiano da 1.2 a 5.0 (vedere tabella). Per le masse dei due oggetti si precisa che m1<m2, e che, mentre l’oggetto m1 si muove di moto rettilineo uniforme con velocità U1 nota, quello m2 è posto, ad ogni prova, fermo in un punto della rotaia tale che: <<…dopo l’urto, le due masse m1 e m2 (i due oggetti di massa m1 e m2) raggiungono (raggiungano) le estremità della rotaia nello stesso tempo>>. Credo che si voglia dire che ad ogni prova con rapporti di massa diversi il contatto-interruttore on venga attivato all’istante dell’urto, mentre, in qualche modo, il contatto stop verrebbe attivato quando i due oggetti di massa m1 con velocità -V1 e m2 con V2 maggiore, toccheranno rispettivamente, per es. l’estremo S1 a sinistra e l’altro l’estremo a destra, nello stesso istante. Ciò implicherebbe che prima di ognuna delle 10 prove con masse diverse, cambiando rapporto fra le masse. dovremmo sapere già dove poggiare sulla rotaia l’oggetto di massa2 ?
Comunque con le precedenti semplificazioni possiamo scrivere, anche noi:
S1=-V1*t ed S2=V2*t e dividendo membra a membro: S1/S2 = -V1/V2
Considerando che un segmento lungo L=230 cm rappresenti la lunghezza della rotaia orizzontale, con un verso a destra. Dopo l’urto l’oggetto m1, che proviene da sinistra, si muoverà verso sinistra rimbalzando con velocità -V1 e quello m2, verso destra con velocità V2 minore (m1<m2), e per ogni rapporto, in tutti i casi, a partire da un dato punto segnato su L più vicino all’estremo destro, i due oggetti raggiungeranno gli estremi della rotaia nello stesso istante.
|
|———————–x————–*——-(L- x)—-| |
—————>
t=x/V1; t=(L-x)/V2 —->x/V1=(L-x)/V2—->V2*x = V1*(L-x)—->V2*x = V1*L-V1*x
x =V1*L/(V2+V1)
Nell’esperimento, sembrerebbe che la diretta proporzionalità fra spazio e velocità e la costanza della quantità di moto scelta prima dell’urto (m1*U1), in tutte le prove, potessero essere la causa dell’uguaglianza di tutte le coppie dei tempi (da approfondire).
Per posizionare m2 è necessario misurare x in anticipo, quindi conoscere L e le due velocità V1 e V2. Si dimostrerà, come segue, che le due velocità sono funzioni delle due masse e della velocità di spinta U1, grandezze già conosciute all’inizio di ogni prova (processo discutibile, vedere dopo)
Applicando i principi della conservazione della quantità di moto e dell’energia cinetica al nostro caso di urto elastico possiamo ricavare V1 e V2 in funzione delle due velocità, della velocità iniziale e di m1 ed m2. Proviamo a risolvere prima il caso più generale con due velocità iniziali U1 e U2 (velocità iniziale di m2) fino ad un certo punto; poi, come vedremo, dalle due equazioni trovate eliminiamo U2 continuando fino al calcolo di V1 e V2 nello specifico nostro caso!
CASO TEORICO PIU’ GENERALE DI URTO ELASTICO NEL QUALE ANCHE U2 SIA DIVERSA DA ZERO
Ora, trattiamo in teoria il caso che, nelle stesse condizioni precedenti, anche la m2 abbia una velocità prima dell’urto, che chiamiamo U2. Otterremo poi la misura degli spazi percorsi nel caso semplificato, azzerando, nelle formule ottenute, U2=0. Il calcolo degli spazi S1 ed S2 è importante perché, in tempi uguali, S1/S2=-V1/V2 e nello studio dell’urto elastico le velocità di rimbalzo, V1 e V2, sono legate alle masse inerziali ed alle velocità iniziali.
Due oggetti di massa diversa m1 ed m2 con velocità U1 e U2 costanti prima dell’urto si scontrano lungo una triettoria rettilinea. Devo trovare V1 e V2 dopo l’urto. Si tratta di due incognite quindi dovrò usare due equazioni. Userò il teorema della conservazione della quantità di moto ed il teorema del conservazione dell’energia cinetica.
Prima equazione → m1U1+ m2U2 = m1V1+ m2V2 *
Seconda equazione → 1/2m1U1^2 + ½ m2U2^2 =1/2m1V1^2+1/2m2V2^2
Rielaboro le due equazioni: tolgo intanto ½ da ogni termine della seconda; porto i termini con m1 sulla sinistra e quelli con m2 sulla destra raccogliendo i due fattori.
Prima equazione → m1(U1-V1) = m2(V2-U2)
Seconda equazione → m1(U1^2-U1^2) =m2(V2^2-U2^2)
Semplifico membro a membro:
U1+V1 =U2 + V2
Con questa equazione e con quella con l’asterisco imposto un sistema a due incognite da cui ricavo le due velocità incognite del rimbalzo elastico
U1 + V1= U2 + V2
m1U1+ m2U2 = m1V1+ m2V2
CASO DELL’ ESPERIMENTO IN OGGETTO
Nel caso del nostro esperimento U2=0, per cui le due equazioni del sistema diventano:
U1 + V1= V2
m1U1 = m1V1+ m2V2
Prima sostituzione
Ricavo dalla prima: V2=U1+V1 e la sostituisco nella seconda:
m1U1 = m1V1+m2U1+m2V1 porto ora nel primo membro il termine con U1 e raccolgo a fattor comune U1 e V1 ottenendo:
U1(m1-m2) = V1(m1+m2) da cui ricavo la prima incognita V1, mentre U1, velocità iniziale di m1, era stata misurata uguale per tutti rapporti U1=(13.7+/-0.3) cm/s) prima.
V1 = (m1-m2)*U1/(m1+m2) (1)
Seconda Sostituzione
Ricavo ora sempre dalla prima: V1=V2-U1 e la sostituisco nella seconda:
m1U1 = m1(V2-U1)+m2V2; cioè: m1U1 = m1V2-m1U1+m2V2
U1(m1+m1) = V2(m1+m2) di qui si ricava la seconda incognita V2
V2 = 2m1*U1/(m1+m2) (2)
All’inizio di ognuna delle 10 prove sembrerebbe di sapere ora piazzare l’oggetto di massa m2 in un punto della rotaia opportuno (individuato da x), avendo calcolato V1 e V2 e avendo misurato da prima U1, la velocità con cui si crea l’urto!
In effetti sorge il dubbio, anche se le due velocità sono state ricavate sul piano teorico, sulla sostenibilità di questa misura di x, perché di fatto le masse sono in questo caso le inerziali, sotto misura, per cui può essere che l’ ipotesi più plausibile (Cellai), per porre m2 in un punto della rotaia, sia procedere ‘per tentativi ed errori’, operazione praticabile sulla nostra apparecchiatura, anche se forse a maggiore entropia. A questo punto si dovrebbe ‘ripulire’ lo scritto da questo ipotetico giro vizioso, prima di proporlo al pubblico? Ma noi, nel dubbio non lo faremo! Praticamente è assente sull’articolo di prof. D’Agostino la sua opinione.
Si potrebbe anche pensare che si possa dimostrare il seguente teorema: se x funziona, allora i due tipi di massa saranno uguali. Cioè attribuendo per ipotesi ad m1 ed m2 inerziali lo stesso valore delle masse gravitazionali corrispondenti, se i due mobili raggiungessero contemporaneamente gli estremi della rotaia, allora verrebbe confermata l’ipotesi stessa. Sarebbe da approfondire e da provare.
D’altra parte è in questa ottica che epistemologi come Antiseri, Medawar ed altri hanno accusato l’articolo scientifico di “frode”. Nel senso che l’articolo scientifico che si legge non fa riferimento al ‘travaglio’ (nel senso della maieutica socratica) della sua costruzione (come anche esemplificato, almeno nel nostro intendimento nel post di questo blog richiamabile con “strani coni”); prima di presentarlo esso viene infatti ripulito e appianato, eliminando i vari sbagli, i ritorni e i punti interrogativi.
Comunque sbagliare e correggersi spesso sono artifici rilevanti dell’apprendimento!
Per arrivare poi alla espressione che lega il rapporto delle due masse inerziali al rapporto degli spazi (S1/S2), il percorso è banale (si fa il rapporto V1/V2 e si uguaglia a -S1/S2, ricavando poi m1/m2).
m1/m2 = 2S1/S2 + 1
Vedere i passaggi nel link:………………DAGOSTINI10001
EPILOGO
Comunque, nel complesso, ci è sembrato un lavoro che ha richiesto un numero esorbitante di prove sperimentali; se abbiamo ben capito almeno 500! (+ altre 10 per il calcolo delle differenze dei rapporti fra masse gravitazionali ed inerziali per fornire il risultato finale: 5.512*10^-4). Si tratta certamente di un corposo lavoro, molto impegnativo e degno di rispetto che, “costretto” in due paginette, non poteva che diventare, almeno per alcuni aspetti, implicito e forse anche po’ criptico (mancanza del disegno della apparecchiatura sperimentale, del calcolo esplicito degli errori, esplicitazione dei percorsi…), a danno della trasparenza per una lettura semplice nelle classi; ma, secondo noi, proprio per queste caratteristiche diventa stimolo alla curiosità, al dibattito ed alla argomentazione critica sui contenuti, aspetti non secondari per l’apprendimento e l’auto-aggiornamento. Non è forse vero che è proprio per questi aspetti che noi abbiamo potuto leggerlo e commentarlo, forse con più attenzione di altri, pur lontano dalla nostra epoca? In conclusione ci auguriamo allora che questa nostra rivisitazione possa servire a stimolare studenti e insegnanti di oggi a ricercare questo lontano, ma ancora rilevante ed attuale, articolo per leggerlo con attenzione (e se possibile, criticarlo) con le loro argomentazioni critiche più ‘affilate’; è così che la conoscenza diventa biologia! Noi, nel leggere questo articolo della Fisica nella Scuola, abbiamo rinverdito un ‘sacco’ di conoscenze!
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Se, in questo blog, da CERCA battiamo il tag “massa gravitazionale ed inerziale“, possiamo leggere altri quattro posts che parlano di queste rilevanti e problematiche grandezze fisiche.
CONCETTO DI TEMPO: Post aperto a vari interventi (dott. prof. Marco Rosa-Clot, dott. Piero Pistoia, dott. ing. Michele Franchi ….,post aperto
Curriculum di piero pistoia:
piero-pistoia-curriculumok (#)
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
L’argomento proposto, da trattare da più punti di vista (scientifico, filosofico, epistemologico, matematico ecc.) oltre al fascino che emana non trascurabile in situazioni di apprendimento, toccando alcune strutture nevralgiche della conoscenza scientifica attuale, è ricco di riferimenti, sottigliezze ed implicazioni anche per la programmazione curricolare, portando all’attenzione degli insegnanti spunti focali di riflessione e discussione (anche sul metodo) nell’ambito delle discipline scientifiche e filosofiche.
LA GRAVITA’, LA TERMODINAMICA ED IL TEMPO
PUO’ L’ORDINE NASCERE DAL CASO?
Chi ha paura del II Principio della Termodinamica?
Dott. Prof. Marco Rosa-Clot
(Professore ordinario di Fisica, Università di Firenze)
SE VUOI LEGGERE L’ARTICOLO DI MARCO ROSA-CLOT CLICCA SU: RosaClot_tempo
PER VEDERE IL CURRICULUM DI ROSA-CLOT CLICCARE SU:
_________________________________________________________
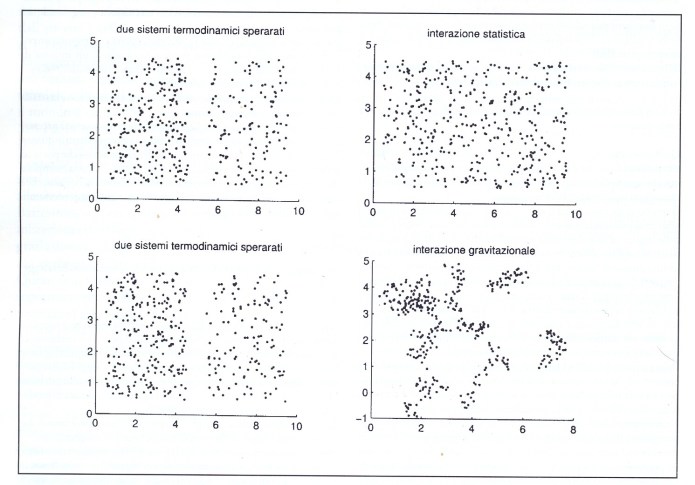
ATTENZIONE! I lettori curiosi, meravigliati da questi articoli, sono in attesa di ricevere (come promesso) da parte del prof. Rosa-Clot informazioni sul programma che permetta di veder girare su tutti i personal computers una simulazione in cui nubi di gas e particelle, pur isolate, evolvono <clusterizzando> (Fig.1)!? I PROMOTORI DEL BLOG
———————————————————————————————
LA FRECCIA DEL TEMPO
Uno dei concetti più densi coglibili nel divenire delle cose
del dott. Piero Pistoia
Versione rivisitata da: ‘Didattica delle scienze’ n.220. Maggio 2002; ‘Didattica delle Scienze’ n.221. Ottobre 2002 e da ‘Il Sillabario’ n.2, 1998.
PER VISIONARE L’ARTICOLO: cliccare su FRECCIA DEL TEMPO2
CURRICULUM DI PIERO PISTOIA CLICCARE SU:
.
______________________________________
SEGUONO DUE BANALI ROUTINES (a: nt=60, n=300 e b: nt=6, n=30) DA COPIARE SULLA CONSOLLE DEL LINGUAGGIO R PER TRACCIARE I CORRISPETTIVI GRAFICI RELATIVI ALLA FRECCIA DEL TEMPO di Piero Pistoia
PRIMA ROUTINE BOZZA
nt=60 # numero molecole nel box di sinistra al tempo zero
n=300 # numero dei passaggi
nc=runif(n, min=0, max=1) # n numeri pseudo-casuali compresi fra 0 e 1
ns=c()
ns=ns[1:n]=0 # azzero gli elementi del vettore ns che registrerà il numero delle presenze nel box di sinistra
ns[1]=nt
for(i in 1:(n-1)){ n1=ns[i]-1/nt # inizia l’algoritmo di MERSENNE TWISTER
if(nc[i]<=n1) ns[i+1]=ns[i]-1 else ns[i+1]=ns[i]+1
}
plot(ns)
PRIMA ROUTINE DEFINITIVA
#COPIA SULLA CONSOLLE DI R
library(graphics)
nt=60
n=300
nc=runif(n,min=0,max=1)
ns=c()
ns=ns[1:nt]=0
ns[1]=nt
for(i in 1:(n-1)){n1=ns[i]/nt
if(nc[i]<=n1) ns[i+1]=ns[i]-1 else ns[i+1]=ns[i]+1
}
x=c(1:n)
par(ask=T)
plot(x,ns,type='l')
# elimino ora circa il 10% degli elementi iniziali che falsano la media e gli errori
# calcolo poi gli errori
v=n/10
ns1=ns[v:n]
x1=x[v:n]
plot(x,ns,type='l',xlim=c(v,n), ylim=c(1,nt))
media_ns1=sum(ns1)/n
media_ns1
errqm_ns1=sqrt(sum((media_ns1-ns1)^2)/n)
errqm_ns1
errel_ns1=errqm_ns1/media_ns1
errel_ns1
# FINE COPIA
RISULTATI DELLA PRIMA ROUTINE
> rm(list=ls(all=TRUE))
> library(graphics)
>
> nt=60
> n=300
> nc=runif(n,min=0,max=1)
> ns=c()
> ns=ns[1:nt]=0
> ns[1]=nt
> for(i in 1:(n-1)){n1=ns[i]/nt
+ if(nc[i]<=n1) ns[i+1]=ns[i]-1 else ns[i+1]=ns[i]+1
+ }
> x=c(1:n)
> par(ask=T)
> plot(x,ns,type='l')
Aspetto per confermare cambio pagina...
>
> # elimino ora circa il 10% degli elementi iniziali che falsano la media e gli errori
> # calcolo poi gli errori
> v=n/10
>
> ns1=ns[v:n]
> x1=x[v:n]
> plot(x,ns,type='l',xlim=c(v,n), ylim=c(1,nt))
Aspetto per confermare cambio pagina...
>
> media_ns1=sum(ns1)/n
> media_ns1
[1] 29.29333
> errqm_ns1=sqrt(sum((media_ns1-ns1)^2)/n)
> errqm_ns1
[1] 4.520068
> errel_ns1=errqm_ns1/media_ns1
> errel_ns1
[1] 0.1543036
> # errore relativo 15 %
FINE RISULTATI PRIMA ROUTINE
SECONDA ROUTINE SENZA IL CALCOLO DEGLI ERRORI (si lascia il loro calcolo al lettore)
library(graphics)
nt=6 # numero molecole nel box di sinistra al tempo zero
n=30 # numero dei passaggi
nc=runif(n, min=0, max=1) # n numeri pseudo-casuali compresi fra 0 e 1
ns=c()
ns=ns[1:n]=0 # azzero gli elementi del vettore ns che registrerà il numero delle presenze nel box di sinistra
ns[1]=nt
for(i in 1:(n-1)){ n1=ns[i]-1/nt
if(nc[i]<=n1) ns[i+1]=ns[i]-1 else ns[i+1]=ns[i]+1
}
ns # 30 valori
x=c(1:30)
plot(x,ns, type=”l”)
—————————————————————————–
IL PROGRAMMA OCTAVE (MATLAB FREE) E LA FRECCIA DEL TEMPO
dott. ing. Michele Franchi, co-fondatore e direttore tecnico di PITOM snc (http://www.pitom.eu)
Attenzione! Nella nuova versione possibile selezionare quanti passaggi iniziali non considerare nei calcoli statistici. Si consiglia di non considerare i primi 100 passaggi. Si consiglia inoltre di non far visualizzare l’animazione nel caso di un elevato numero di iterazioni e/o molecole. L’animazione fa si che la simulazione rallenti moltissimo già nel caso di 200 iterazioni e 10 molecole.
Usiamo il programma Octave per ‘costruire’ il grafico della Freccia del Tempo di Boltzmann.
ISTRUZIONI
1) Installare Octave, scaricandolo gratuitamente da Internet.
2) Ricopiare gli scripts che seguono, anche con copia-incolla, per es. nel Blocco Note e memorizzarli poi col nome ‘frecciaDelTempo.m’ ed ‘animationPlot.m’ in una directory aperta nel proprio PC, per es. in C 
octaveScript.
SCRIPTS DELLA FRECCIA DEL TEMPO IN OCTAVE ‘ File “frecciaDelTempo.m”
clc clear all disp('############################# ') disp('# [START] Freccia Del Tempo # ') disp('############################# ') disp('') disp('') % INIZIALIZZAZIONE VARIABILI n = 0; % [Ingresso] Numero di iterazioni da calcolare nd = 0; % [Ingresso] Numero iniziale di molecole nel box DX nt = 0; % Numero totale di molecole n1 = 0; % Probabilità di attraversamento di una molecola da SX a DX media = 0; % Media del numero di molecole nel box SX devStd = 0; % Deviazione standard del numero di molecole nel box SX err = 0; % Coefficiente di variazione del numero di molecole nel box SX stat_start = 0; % Campione iniziale da cui calcolare le statistiche aux = 1; % Variabile ausiliaria di sistema while (aux == 1) n = input ("Quante iterazioni vuoi calcolare (N)? [200...4000]\n"); aux = 0; if (n > 4000) disp('') disp('[WARNING] Attenzione il dato inserito risulta maggiore di 4000') disp('Reinserirlo...') aux = 1; else if (n < 200) disp('') disp('[WARNING] Attenzione il dato inserito risulta minore di 200') disp('Reinserirlo...') aux = 1; else disp('OK!') end end disp('') end ns = zeros(1,n); %[Ingresso] Numero iniziale di molecole nel box SX aux = 1; while (aux == 1) stat_start = input (strcat("Quanti campioni iniziali vuoi escludere dalle statistiche? [1...",num2str(n),"]\n")); aux = 0; if (1 > stat_start) disp('') disp('[WARNING] Attenzione il dato inserito risulta minore di 1') disp('Reinserirlo...') aux = 1; else if (n < stat_start) disp('') disp(strcat("[WARNING] Attenzione il dato inserito risulta maggiore di (",num2str(n),")")) disp('Reinserirlo...') aux = 1; else disp('OK!') end end disp('') end aux = 1; while (aux == 1) ns(1) = input ("Quante molecole ci sono inizialmente nel box di sinistra?\n"); aux = 0; if (ns(1)<0) disp('') disp('[WARNING] Il numero di molecole deve essere maggiore o uguale a 0...') aux = 1; else disp('OK!') end disp('') end aux = 1; while (aux == 1) nd = input ("Quante molecole ci sono inizialmente nel box di destra?\n"); aux = 0; if (nd<0) disp('') disp('[WARNING] Il numero di molecole deve essere maggiore o uguale a 0...') aux = 1; else disp('OK!') end disp('') end aux = 1; while (aux == 1) enable_animation = input ("[Sconsigliato per un numero elevato di iterazioni e/o molecole]\nVuoi vedere l'animazione [s/n]?\n","s"); aux = 0; enable_animation = strtrim(enable_animation); if~(strncmpi(enable_animation,"s",1)||strncmpi(enable_animation,"n",1)) disp('') disp('[WARNING] Non ho capito...') aux = 1; else disp('OK!') end disp('') end % Calcolo molecole totali nt = ns(1) + nd; disp('') disp('@@@@@@@@@@@@@@@@@@@@@@@@@') disp('@ INIZIO LA SIMULAZIONE @') disp('@ ATTENDERE! @') % Per ogni iterazione... for i = 1:(n) % Calcolo probabilità attraversamento molecola SX -> DX n1 = ns(i)/nt; % Se non siamo nell'ultima iterazione... if (i < n) % ...se la probabilità calcolata è... % ...minore o uguale di un numero randomico uniformemente distribuito... % ...nell'intervallo (0,1) [Mersenne Twister algorithm with a period of 2^19937-1]... if (rand <= n1) % ...avviene il passaggio di una molecola da SX a DX ns(i+1) = ns(i)-1; % ...altrimenti... else % ...avviene il passaggio di una molecola da DX a SX ns(i+1) = ns(i)+1; end end end % Calcolo la media del numero di molecole a SX a partire dal campione "stat_start" media = mean(ns(stat_start:n)); % Calcolo la deviazione standard del numero di molecole a SX a partire dal campione "stat_start" devStd = std(ns(stat_start:n)); % Calcolo il coefficiente di variazione del numero di molecole nel box SX er = devStd/media; disp('@ SIMULAZIONE TERMINATA @') disp('@@@@@@@@@@@@@@@@@@@@@@@@@') disp('') disp("Risultati statistici relativi al numero di molecole nel box SX:") disp(strcat("Media:\n",num2str(media))); disp(strcat("Deviazione standard:\n",num2str(devStd))); disp(strcat("Coefficiente di variazione:\n",num2str(er))); % GRAFICI if(strncmpi(enable_animation,"s",1)) animationPlot(ns,n,nt) end figure plot(1:n,ns) titlePlot = strcat("SIMULAZIONE DI BOLTZMAN\nmedia = ",sprintf("%6.3f", media),";",... " devStd = ",sprintf("%6.3f", devStd),";",... " er = ",sprintf("%6.3f", er),";\n",... " ns = ",num2str(ns(1)),";",... " nd = ",num2str(nd),";",... " passaggi = ",num2str(n)); title(titlePlot) ylabel ("N. molecole box SX"); xlabel ("Iterazioni (i)"); drawnow; % SALVATAGGIO SU FILE currentDateTime = strftime ("%Y-%m-%d_%H-%M-%S", localtime (time ())); currentParameters = strcat ("_Prameters_",num2str(ns(1)),"_",num2str(nd),"_",num2str(n)); filename = strcat(currentDateTime,currentParameters,".csv"); % Salvo nella cartella di lavoro un file con i valori del vettore ns nella prima colonna % Il nome del file è del tipo "aaaa-mm-gg_hh-mm-ss_Parameters_ns(1)_nd_n.csv" dove: % aaaa-mm-gg_hh:mm:ss --> sono la data e l'ora di creazione del file % ns(1) --> è il numero iniziale di molecole nel box SX % nd --> è il numero iniziale di molecole nel box DX % n --> è il numero di iterazioni scelto dlmwrite (filename, ns', ';') disp('') disp('') disp('########################### ') disp('# [END] Freccia Del Tempo #') disp('########################### ') disp('') disp('')File “animationPlot.m”
function animationPlot (ns_array,n_step,nt) figure box_width = 10; box_height = 10; box_X_points = 0:1:box_width; box_Y_points = 0:1:box_height; plot(box_X_points,box_height*ones(box_width+1,1),'-k','LineWidth',4); hold on plot(box_X_points,0*ones(box_width+1,1),'-k','LineWidth',4); hold on plot(box_width*ones(box_width+1,1),box_Y_points,'-k','LineWidth',4); hold on plot(0*ones(box_width+1,1),box_Y_points,'-k','LineWidth',4); hold on plot((box_width/2)*ones(2,1),[box_height, (box_height/2)+1],'-k','LineWidth',4); hold on plot((box_width/2)*ones(2,1),[0, (box_height/2)-1],'-k','LineWidth',4); hanlder_mol = zeros(nt,1); handler_title = 0; for step = 1:n_step num_mol_SX = ns_array(step); num_mol_DX = nt - num_mol_SX; if(step > 1) delete(handler_title); end handler_title = title(strcat("N. SX: ",num2str(num_mol_SX)," N. STEP: ",num2str(step), " N. DX: ",num2str(num_mol_DX))); for i = 1:nt hold on if(step == 1) if(i <= num_mol_SX) hanlder_mol(i) = plot(((box_width/2)-1)*rand() + 0.5,(box_height-1)*rand() + 0.5,'or','MarkerEdgeColor','r'); else hanlder_mol(i) = plot((box_width/2) + ((box_width/2)-1)*rand() + 0.5,(box_height-1)*rand() + 0.5,'ob','MarkerEdgeColor','b'); end else if(i <= num_mol_SX) set(hanlder_mol(i),'XData',((box_width/2)-1)*rand() + 0.5,'YData',(box_height-1)*rand() + 0.5,... 'MarkerEdgeColor','r'); else set(hanlder_mol(i),'XData',(box_width/2) + ((box_width/2)-1)*rand() + 0.5,'YData',(box_height-1)*rand() + 0.5,... 'MarkerEdgeColor','b'); end end end drawnow; end endfunction3) Lanciare Octave 3.1) Impostare come directory di lavoro quella contenente lo script con il comando (es. digitare nella shell di Octave ‘cd c:\octaveScript’) 3.2) Lanciare lo script scrivendo nella shell il nome del file (‘frecciaDelTempo’) 3.3) Inserire i dati richiesti 3.4) Nella directory di lavoro impostata verrà creato un file con formato del nome “aaaa-mm-gg hh:mm:ss media_devStd_er%_ns(1)_nd_n.csv” dove: aaaa-mm-gg hh:mm:ss –> sono la data e l’ora di creazione del file ns(1) –> è il numero iniziale di molecole nel box SX nd –> è il numero iniziale di molecole nel box DX n –> è il numero di iterazioni. Questo file conterrà nella prima colonna il numero di molecole presenti nel box di sinistra ad ogni iterazione. Il file è in formato csv ed utilizza il ‘;’ come separatore. ATTENZIONE: IN OCTAVE I NOMI SONO CASE SENSITIVE, OVVERO SI FA DISTINZIONE TRA LETTERE MAIUSCOLE E MINUSCOLE. ATTENZIONE: SI RACCOMANDA DI UTILIZZARE CARTELLE CON PERCORSI SENZA SPAZI O CARATTERI PARTICOLARI. Dopo un certo tempo (quindi alla fine delle immissioni attendere!) che varia con il numero dei passaggi scelto apparirà il grafico del numero delle molecole di sinistra col tempo. Da continuare Dobbiamo aggiungere a questo post altri articoli sul concetto di tempo!
Testi rivisitati da ‘Il Sillabario’ già incontrati sul blog
Testo rivisitato da il ‘Sillabario’ n.
Il sillabario 2013 