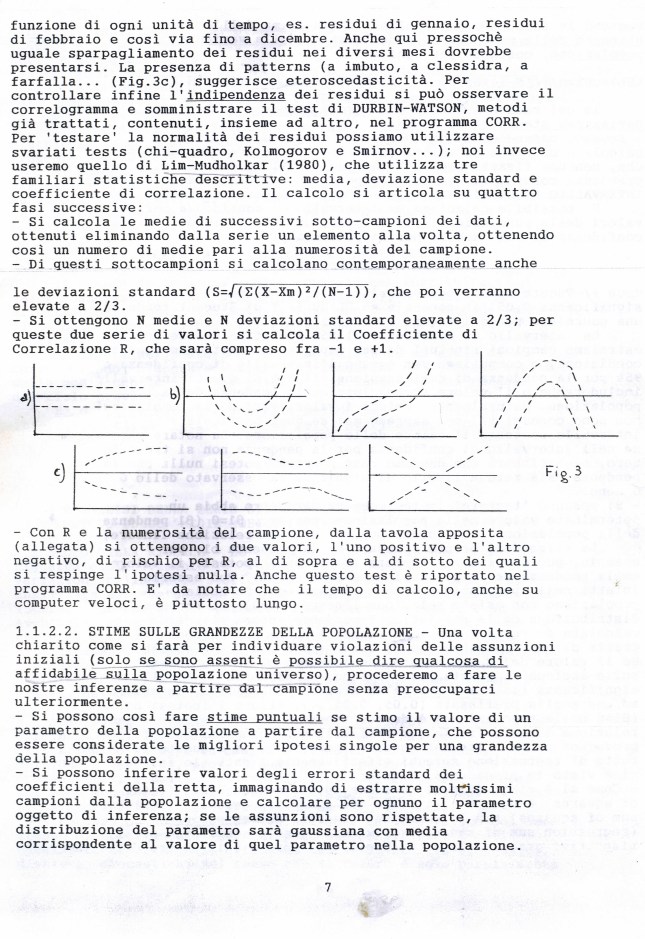
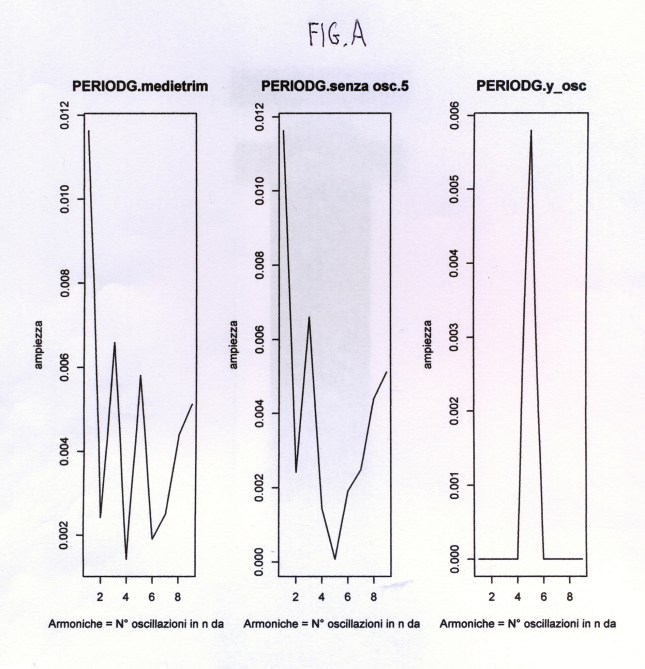
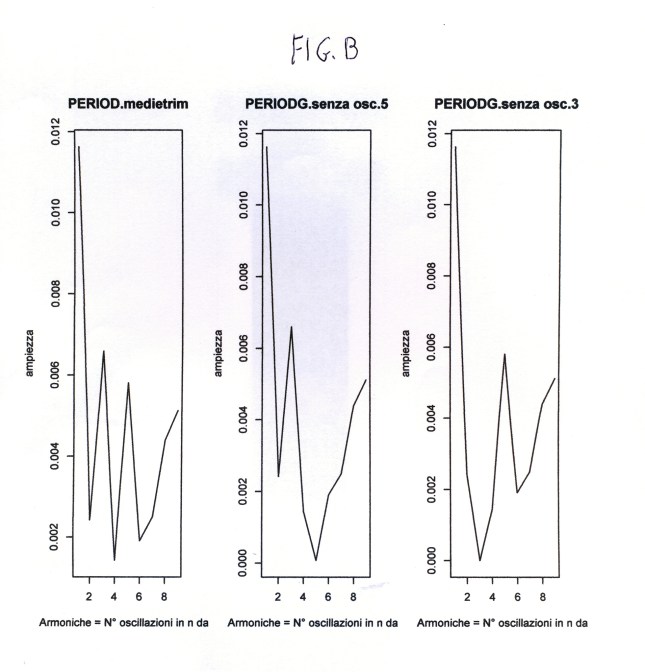
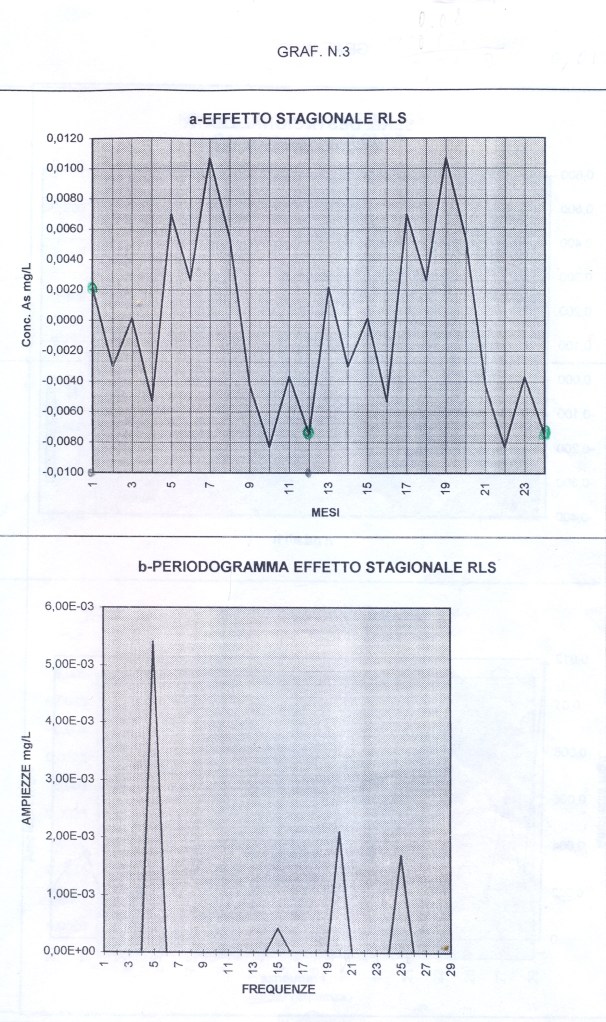
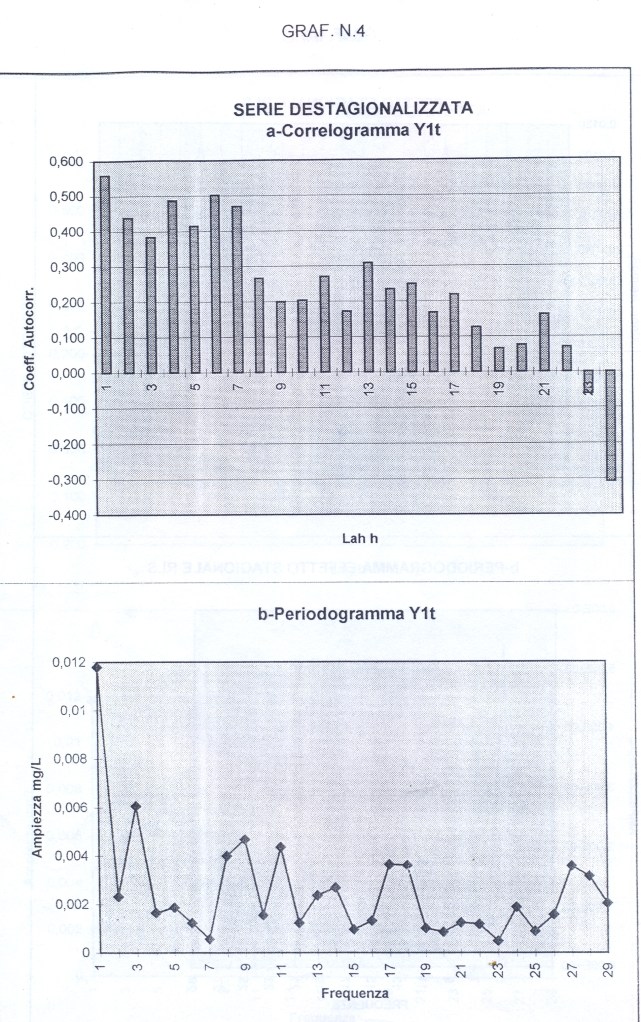
Questo progetto è piaciuto al blog Agenda19892010 come comunicato il 2-6-2015 da WordPress all’Amministratore con una e-mail. E’ piaciuto anche al blog Briciolanellatte come comunicato il 9-6-2015 da WordPress all’Amministratore con una mail.
_________________________________________________________
piero-pistoia-curriculumok (#)
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
PREMESSA
ATTENZIONE: QUALORA, IN QUESTO ARTICOLO PUBBLICATO SU INTERNET, ALCUNE FOTO (non sappiamo il perché!) NON APPAIANO, LASCIANDO SPAZI BIANCHI, O APPAIONO, MA A BASSA RISOLUZIONE, BASTA CLICCARE SU ESSI PER FAR APPARIRE LE FOTO INGRANDITE E CHIARE! PER TORNARE INDIETRO ANNULLARE IL CARICAMENTO DELLA FOTO.
N.B. – SE NON PRECISATO ALTRIMENTI, TUTTE LE FOTO, PROGETTI, SCRITTI, ARGOMENTAZIONI E COMMENTI SONO DEL COORDINATORE PIERO PISTOIA
CURRICULUM DI PIERO PISTOIA:
piero-pistoia-curriculumok (#)
CHI E’ L’AUTORE (traccia): Curriculum di Piero Pistoia
Piero Pistoia, diplomato negli anni ’50 presso il Liceo Classico Galileo Galilei di Pisa, è dottore in Scienze Geologiche con 110/110 e lode, discutendo una tesi di geofisica e, da borsista, ha lavorato e pubblicato presso l’Istituto di Geologia Nucleare di Pisa, misurando le età degli “strani” graniti associati alle ofioliti (1) e studiando i serbatoi di gas e vapori della zona di Larderello. Successivamente ha scritto una cinquantina di articoli pubblicati a stampa, a taglio didattico-epistemologico, di cui circa la metà retribuiti secondo legge, dagli editori Loescher, Torino, (rivista “La Ricerca”), La Scuola di Brescia (“Didattica delle Scienze”), a controllo accademico ed altri, affrontando svariati problemi su temi scientifici: dall’astrofisica all’informatica, dall’antropologia culturale all’evoluzione dell’uomo, dalla fisica alla matematica applicata e alla statistica con il supporto di migliaia di linee di svariati programmi in linguaggi come Mathematica di Wolfram, R, SPSS, dalla geologia applicata al Neoautoctono toscano, dall’origine dell’Appennino alla storia delle ofioliti, alle mineralizzazioni delle antiche cave in Val di Cecina (in particolare su calcedonio, opale e magnesite) ecc.. En passant, ha scritto qualcosa anche sul rapporto Scienza e Poesia, sul perché la Poesia ‘vera’ ha vita infinita (per mere ragioni logiche o perché coglie l’archetipo evolutivo profondo dell’umanità?); ha scritto alcuni commenti a poesie riprese da antologie scolastiche e, infine decine di ‘tentativi’ poetici senza pretese. Molti di tali lavori sono stati riportati su questo blog. (2)
NOTE
(1) L’età dei graniti delle Argille Scagliose, associati alle ofioliti, al tempo alla base della falda in movimento, corroborò sia l’ipotesi che esse fossero ‘strappate’ dal basamento ercinico durante i complessi eventi che costruirono la catena appenninica, sia, indirettamente, rafforzò la teoria a falde si ricoprimento nell’orogenesi appenninica. Fu escluso così che il granito associato alle ofioliti derivasse, almeno non in tutti i casi, da una cristallizzazione frazionata (serie di Bowen) da un magma basico od ultrabasico.
(2) Piero Pistoia ha superato concorsi abilitativi nazionali, al tempo fortemente selettivi (cioè non frequentò mai i famigerati Corsi Abilitanti, fortemente voluti dai sindacati dei docenti!), per l’insegnamento, in particolare, nella Scuola Superiore per le seguenti discipline: Scienze Naturali, Chimica, Geografia, Merceologia, Agraria, FISICA e MATEMATICA. Le due ultime materie sono maiuscole per indicare che Piero Pistoia in esse, in tempi diversi, fu nominato in ruolo, scegliendo poi la FISICA, che insegnò praticamente per tutta la sua vita operativa.
Pochi anni prima che l’ITIS di Pomarance fosse aggregato al Commerciale di Volterra, il dott. prof. Piero Pistoia fu nominato Preside Incaricato dal Provveditorato agli studi di Pisa, ottenendo il massimo dei voti sulla attività svolta.
Così la parte scritta di questo Post, nel bene e nel male, è a cura di Piero Pistoia che auspica critiche, suggerimenti, correzioni, integrazioni.
NEL MALE CI SI CORREGGE! SE E DOVE SI CORREGGE, SPECIALMENTE LI’, SI IMPARA!
COL TEMPO FORSE FAREMO DEGLI INDICI E DEI RIMANDI INIZIALI PER MUOVERCI NON IN MANIERA SERIALE ALL’INTERNO DEL POST
Procederemo al solito discutendo e argomentando non tanto per ‘comunicare’ quanto per ‘costruire’ insieme questo tipo di conoscenza come suggerisce Foerster. L’obbiettivo è esclusivamente didattico-culturale, per cui questo materiale può essere utilizzato da tutti gratuitamente nel modo che scegliamo (eccetto i disegnetti schematici trasferiti dai testi di riferimento); in particolare, auspichiamo venga scoperto e utilizzato in qualche modo dalla Scuola.
I TRE CURATORI ‘COSTRUISCONO’ IN TEMPO REALE PER CUI NON GARANTISCONO CHE I CONCETTI, SEMPRE IN VIA DI APPROFONDIMENTO E MODIFICA, POSSANO ESSERE DEFINITIVI E CORRETTI
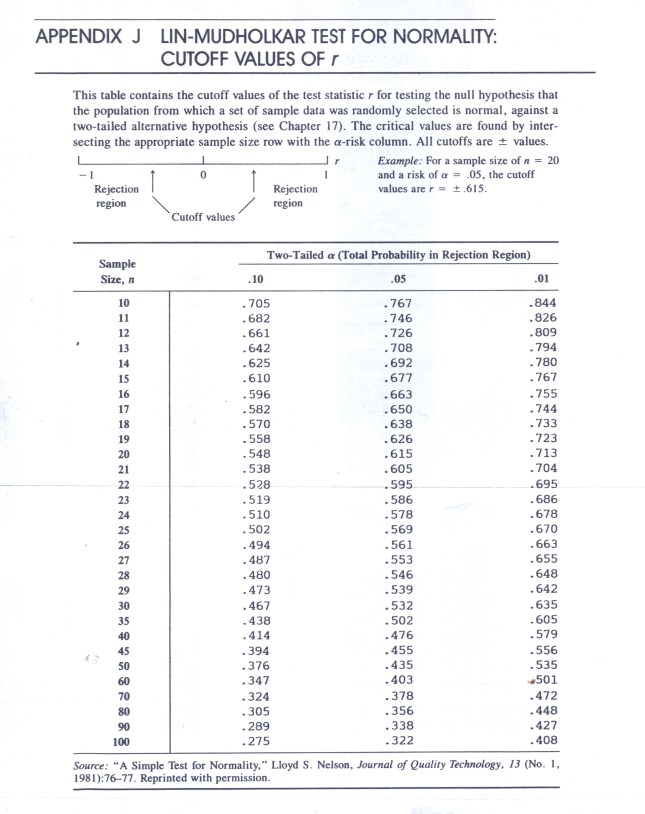
I TESTI QUALIFICATI DI RIFERIMENTO PER QUESTO LAVORO SONO PRINCIPALMENTE I SEGUENTI (consigliamo i lettori di procurarseli per i riferimenti, l’approfondimento di questo post e la qualificazione delle biblioteche personali!) :
EUGENIO BARONI “GUIDA BOTANICA D’ITALIA” Ed. CAPPELLI
PIETRO ZANGHERI “FLORA ITALICA Vol. I-II-III” Ed. CEDAM
SANDRO PIGNATTI “FLORA D’ITALIA Vol. I-II-III” Ed. EDAGRICOLE
EDUARD THOMMEN “ATLAS DE POCHE DE LA FLORE SUISSE” EDITIONS BIRKHAUSER BALE.
Si allegano anche foto di qualche pagina ripresa da un interessante libro, con schizzi originali affiancanti lo scritto sintetico e rilevante, a firma di due ricercatrici dell’Istituto Botanico dell’ Università di Pisa, A.M. Pagni e G. Corsi, stampato da Arti Grafiche Pacini Mariotti, Pisa che ringraziamo.
VENGONO ANCHE CONSULTATE DUE GROSSE ENCICLOPEDIE SUL REGNO VEGETALE, L’UNA EDITA DA VALLARDI E L’ALTRA DA RIZZOLI; E SVARIATI ALTRI TESTI SECONDARI DI DIVERSE CASE EDITRICI CHE NOMINEREMO QUANDO NECESSARIO.
A questi testi si farà continuamente riferimento esplicito e si spera che Autori ed Editori permetteranno di trasferire qualche disegno schematico di chiarimento dai loro testi a questo post, il cui unico obiettivo è e rimarrà solo quello di ‘costruire’ e comunicare didatticamente cultura, per quanto ci riesce, sempre del tutto gratis. Questo blog non ha alcun fine di lucro ed è auto-finanziato. Comunque siamo disponibili nell’immediato a qualsiasi intervento su questo post su avvertimento (al limite, se necessario, anche a sopprimerlo!)
_______________________________________________________
UNA DEDICA NECESSARIA (NDC: Piero Pistoia)
La mia idea di scegliere un percorso botanico accessibile alle Scuole fu discussa in una serie di incontri sul rapporto Scuola/Natura con un genuino naturalista empatico e poeta locale, il maestro Giuseppe Zanella, che dedicò tutta la vita a studiare i comportamenti di animali e vegetali con grande intuito, sensibilità e rispetto per la Natura e l’Universo. Fece numerose pubblicazioni per importanti case editrici e articoli per note enciclopedie. Stavamo per iniziare in concreto il lavoro, quando sfortunatamente si ammalò irreversibilmente. Di questo personaggio, secondo me, di rilevante spessore, mi rimane un grande e affettuoso ricordo di amicizia e di stima e mi sento di dedicare questo nostro lavoro floristico alla Sua memoria.
Dott. PIERO PISTOIA, coordinatore.
_________________________________________
POST SPERIMENTALE IN VIA DI COSTRUZIONE – Intanto iniziamo con un primo tentativo di percorso. Sul percorso mensilmente si osserveranno, si fotograferanno e descriveranno per la classificazione le nuove piantine ‘che vediamo’ e ad ‘ogni giro’ cercheremo anche di descrivere alcune di ‘quelle di base’. Possibilmente su ogni piantina verrà attivata una discussione anche tornando indietro. Chiaramente il ciclo mensile copre 12 mesi, ma… ogni anno si rinnova, per cui questo post rimarrà aperto all’infinito, naturalmente finché gli autori non si stancheranno!
LA CARTINA DEL PERCORSO

 Il podere da cui inizia (o finisce) la vicinale Sant’Anna (nel senso che è riportata l’indicazione ufficiale) si chiama P. Poggio Bartolino, subito prima della deviazione Podernuovo-Poggio Bianco.
Il podere da cui inizia (o finisce) la vicinale Sant’Anna (nel senso che è riportata l’indicazione ufficiale) si chiama P. Poggio Bartolino, subito prima della deviazione Podernuovo-Poggio Bianco.
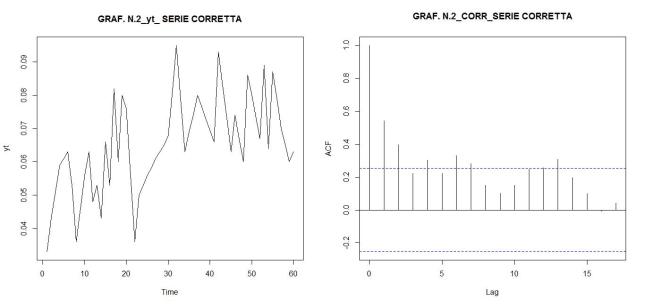
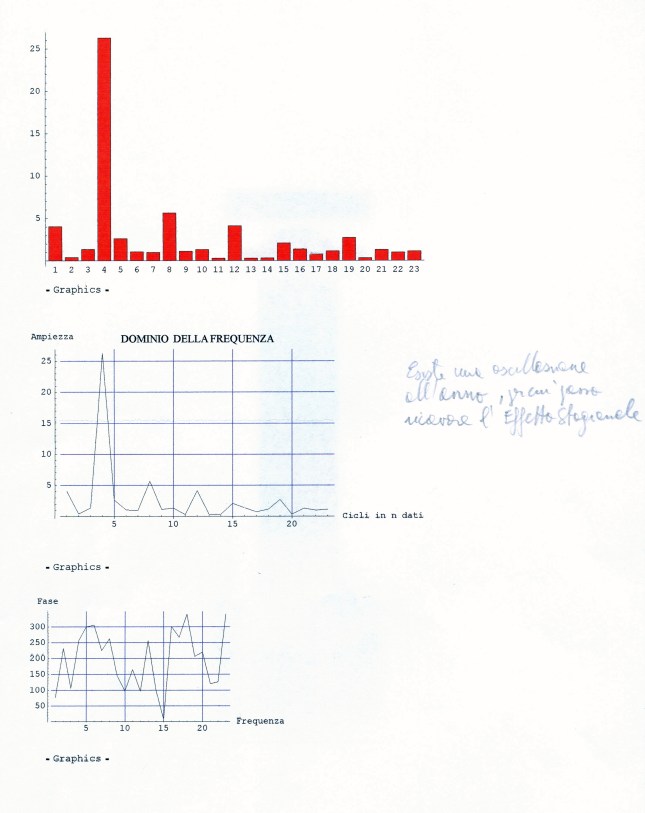
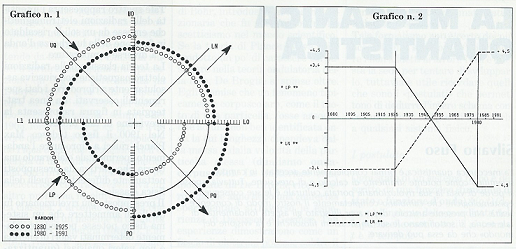
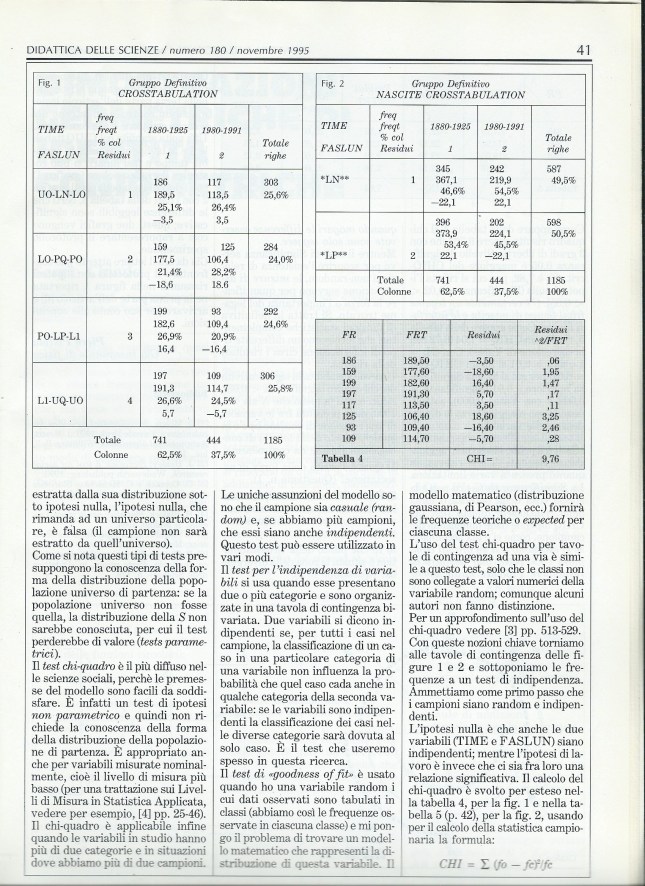
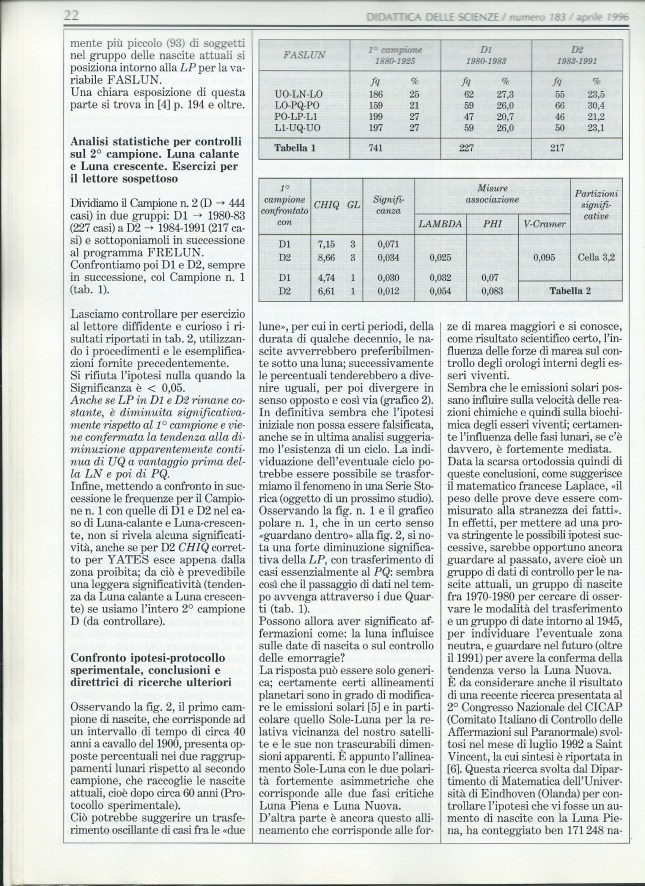
Un’erbaccia spontanea abbondante in settembre-ottobre 2015 è stata oggetto di discussione sulla sua classificazione: Erigeron bonariensis o Conyza bonariensis (=Erigeron linifolium)? Per anticipare o rivedere le argomentazioni del coordinatore P. Pistoia, cliccare sulla parola ‘calda’ di seguito (in effetti sembra che Erigeron bonariensis non appaia nei testi consultati).
ERIGERON o CONYZA?
_______________________________________
Per vedere altri schemi per la sua classificazione, controllare il anche link ‘Althea cannabina’ nella PARTE QUARTA, per un confronto con Malva alcea.
ALCUNE FOTO IN ANTEPRIMA
(Le foto di Cristina Moratti sono riportate anche sul blog “La carrozza del Gambini”)
Quattro Foto di due piantine (Orchidea apifera, Erba vajola) del percorso sperimentale eseguite da Cristina Moratti
 Ophrys apifera (fioritura maggio)
Ophrys apifera (fioritura maggio)
Cristina ha fotografato l’orchidea vicino al P. San Domenico
La Borraginacea Cerinthe maior, è stata classificata da Angelo Bianchi, Erborista. Si notano sulle foglie tracce di strutture ghiandolari.
La Cerinthe si poteva vedere, poco tempo fa, nel tratto, a sinistra del percorso, in cui la strada vicinale di Sant’Anna, dopo breve salita oltre il P. Il Ponso, piega scendendo verso Poggio Bartolino; sarebbe stata presente dalla primavera all’autunno, come accadde lo scorso anno.
In effetti a fine Maggio 2015 la stazione a Cerinthe è stata soppressa; era nata sul percorso del trattore. La rivedremo il prossimo anno? O forse prima?
————————————————-
LA ROSASEA FILIPENDULA (SPIRAEA) exapetala
Due Foto di una piantina (Filipendula) del percorso sperimentale, di Cristina Moratti e Piero Pistoia rispettivamente

Si tratta della Rosacea Filipendula (Spiraea) exapetala, classificata da Piero Pistoia; la piantina era diffusa praticamente lungo tutto il percorso, in particolare davanti a Poggio Bartolino (prima del taglio dei margini); fioritura nella seconda metà di Maggio; da giugno sembra scomparsa sono rimaste solo le tracce delle foglie basali.
Quella che segue è la foto di Cristina Moratti di una Crucifera (Brassicacaea) del genere Alyssum caratteristica delle ofioliti (A. bertolonii), che fa parte di una interessante stazione floristica fotografata (una ventina di pianticelle che vivono o vivono anche sulle ofioliti) e classificata e commentata dalla stessa Cristina sul blog “La carrozza del Gambini”. Questa pianticella viene riportata in questo percorso sperimentale perché mi sembra che fosse quella che in autunno del 2014 stranamente faceva, se ben mi ricordo, bella vista sul lato destro della strada Sant’Anna una decina di metri prima che deviasse scendendo verso Poggio Bartolino ed alcune anche davanti allo stesso podere Sant’Anna. L’ipotesi, se fosse stato un Alisso, fu che qualche cercatore di funghi del posto calpestando gli ofioliti (leggere su questo blog il post a più voci sulla ‘strana storia’ di queste rocce) della macchia di Monterufoli abbia riportato semi su questa bancata argillosa a ciottoli silicei del Neoautoctono (se vuoi approfondire cerca ‘Neoutoctono’ su questo blog)! Attualmente nel percorso non ho notato pianticelle simili a quella che nel ricordo mi sembrava un Alyssum; vedremo in autunno se ricrescerà, in modo da poter controllare! Sarebbe interessante comunque che Cristina, agganciando una mappa topografica, da fornire nel suo blog, ad una strada percorribile con la macchina, descrivesse il posto di questa stazione con una tolleranza di qualche metro, in maniera che possa essere resa visitabile ad hoc. Per es., una scolaresca nelle ore di lezione della mattinata potrebbe, come obbiettivo didattico specifico, visitarla in qualche ora e tornare a lezione.
DIGRESSIONE PER ASSIMILARE LE IDEE E CORREGGERE QUELLE CHE CREANO FAILLANCE
Digressione sulle piante delle ofioliti e in particolare sull’Alissum. La proposta sarebbe di costruire un articolo scritto in Word o con Open Office dal titolo per es. “Osservazione, descrizione e classificazione delle piantine endemiche delle Ofioliti”. Dopo il titolo si potrebbe inserire dal menù del word processor scelto una o più foto di insieme. …..Successivamente si inserisce nel testo, per es., la foto dell’Alissum, e si scrivono nel testo sotto quali sono le caratteristiche importanti per la classificazione inserendo ogni volta le loro foto (forma delle foglie, distribuzione sul caule, foto del fiore singolo ecc.) e questo in successione per ogni piantina. E’ un lavoro lungo da fare a ‘pezzi’ aggiornando con calma!
PREMESSA a cura del dott. Piero Pistoia
L’idea è di scegliere un percorso di circa un’ora andata e ritorno (consistente con l’utilizzo anche da parte delle scolaresche) che “apra” alla campagna, meglio se già utilizzato dai cittadini per passeggiate, footing, ecc.. Immaginiamo di dividerlo in tratti con riferimenti topologici riconoscibili e che abbiano significato per le pianticelle della flora spontanea che qui vivono (almeno finchè il Comune non deciderà di tagliare l’erba ai margini della strada). L’idea si basa anche sull’ipotesi che le piantine, anche se tagliate, abbiano una probabilità superiore a quella fornita dal caso di ricrescere circa nella stessa zona. Come primo tentativo, abbiamo scelto una successione di tratti che partendo dall’inizio di via Mazzolari, zona verde davanti alla proprietà Scarciglia (stazione floristica a Salvia sclarea ed altro; si vedano, per es. al recinto, i cartelli alle varie piante della macchia mediterranea), attraverso via del Poderino, scende a via dei Filosofi e, verso sud-est, incrocia la strada chiusa che porta a sud verso il Podere Sant’Anna, il P. San Vittore e il P. Il Ponso e, oltre il poggetto, scende verso sud-est fino a Poggio Bartolino dove ha termine la vicinale Sant’Anna e poi ancora verso sud nella strada sterrata che porta al bivio per il Podere Il Mirto e a Poggio Bianco (vedere la carta topografica riportata di questi posti).
Durante la costruzione, introdurremo, quando si rendono disponibili, le foto delle diverse pianticelle mese per mese da riordinare di volta in volta, attribuendole ai diversi tratti di strada.
Le seguenti due sezioni della carta topografica del paese di Pomarance (scala originale 1=5000) che contengono il percorso descritto evidenziato in giallo, sono state integrate con i nomi dei tratti di strada, che compongono il percorso stesso ed altro (individuazione scuole, edifici rilevanti, riferimenti alla posizione floristica ecc.). Per la carta topografica e per la gentilezza e disponibilità dimostrate dobbiamo ringraziare il tecnico dell’Ufficio del Comune, la geometra Signora Cabiria Pineschi Gazzarri. Da notare come la carta non sia aggiornata; è poco evidenziato, per es., scendendo per la vicinale Sant’Anna, a circa un centinaio di metri dall’incrocio con Via dei Filosofi, sulla destra lo stradello per il P. San Pietro (da aggiungere).
LA CARTINA DEL PERCORSO
Il podere da cui inizia la vicinale Sant’Anna (nel senso che è riportata l’indicazione ufficiale) si chiama P. Poggio Bartolino, subito prima della deviazione Podernuovo-Poggio Bianco.
Le foto immesse non sono ottimali, ma non sono definitive; ne cercheremo di migliori.
DIARIO FLORISTICO DA AGGIORNARE NEL CORSO DEL MESE DI MAGGIO 2015
DIARIO FLORISTICO AGGIORNATO GIORNO PER GIORNO NEL CORSO DEL MESE DI GIUGNO 2015
ALLA FOTO DI UN ELEMENTO EMBLEMATICO DI OGNI SPECIE (O GENERE) VERRA’ AGGIUNTA UNA BREVE SCHEDA TRASFERIBILE, UTILE PER LA SUA IDENTIFICAZIONE
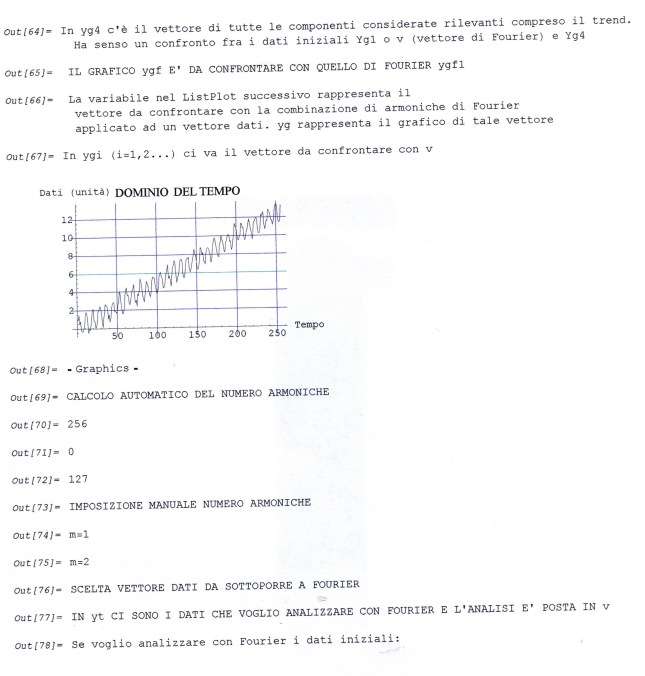
TUTTE LE FOTO, CHE NON RIPORTANO IL NOME DI UN AUTORE, SONO STATE SCATTATE DA PIERO PISTOIA
– rara la salvia selvatica
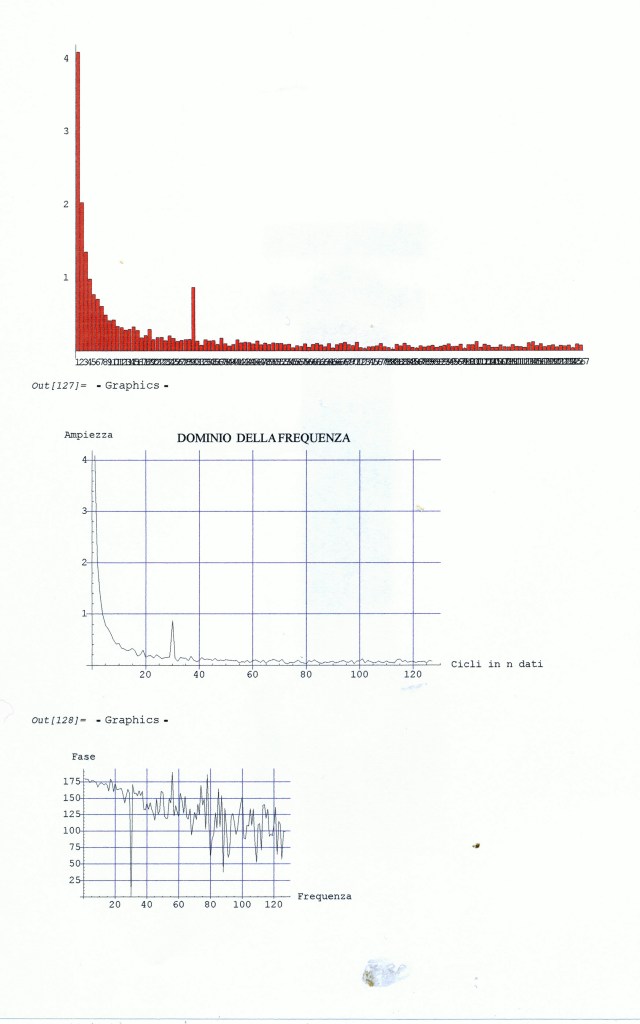
– A partire da giugno della Filipendula rimangono praticamente solo le foglie
LA GENTIANACAEA CHLORA perfoliata
– Primi di giugno fioritura della Chlora perfoliata oltre il cartello per podere Il Mirto, scendendo verso Poggio Bianco a metà del tratto; da fare foto. Sull’argine destro, a scendere, dinanzi al P. Sant’Anna.
Non individuata ancora la Gentianacea Erytraea centaurium, vista in estate un anno fa.
L’HIPERICUM perforatum
– si mantiene fiorito ancora Hipericum perforatum

IL PROBLEMA DELLA SCROPHULARIACAEA VERBASCUM blattaria
– fiorito da poco un verbasco (?), unico stelo glabro con foglie a triangolo isoscele a lati leggermente curvi e seghettati (?); più grandi ed ovali-ellittiche debolmente picciolate (non inserite direttamente sul ramo, ma tramite un corto peduncolo) quelle basali, sempre più piccole e sessili (inserite direttamente sul ramo) quelle superiori (foglie cauline) tendenti ad abbracciare il caule con la parte inferiore; Verbascum blattaria? Il famoso Verbasco delle falene? Fare foto e classificare; questi individui sono visibili nel tratto verso Poggio Bianco dopo il cartello per il P. Mirto, a sinistra prima dello stradello che scende a destra nel campo. Sembra esista un solo esemplare, la settimana scorsa (10-6), in questo tratto, ne vidi 4 o 5. Oggi 18 giugno, questo esemplare è stato tagliato, mentre è visibile un’altra piantina col fiore qualche metro sotto il tasso barbasso (vedere sotto) scendendo, a sinistra, sulla stessa sterrata (vedere foto). Sembra siano appena nati altri esemplari in questi giorni in cima al poggetto sopra il P. Il Ponso, sulla sinistra salendo. Oggi (18) uno di essi ha messo il fiore.
 Si notano in basso foglioline pentafille forse di Potentilla
Si notano in basso foglioline pentafille forse di Potentilla
La foto che segue riporta un individuo di V. blattaria (?) del poggetto; si notano alcuni esemplari di Papaver rheas
La foto che segue è stata scattata l’anno scorso sullo stesso percorso e circa lo stesso periodo; assomiglia alla precedente?
Uno sguardo al futuro…….
Abbiamo fotografato, dopo anni (2 giugno 2019) ancora piantine di Verbascum blattaria nel nostro percorso, scendendo, davanti alla proprietà Sant’Anna….
LA SCROPHULARIACAEA VERBASCUM thapsus
Di seguito in vegetazione un ‘individuo’ di Verbascum thapsus (con cartello in perallum) appare sempre sulla deviazione per Poggio Bianco a sinistra scendendo, a metà tratto.

Verbascum tapsus scendendo nella sterrata qualche metro dopo l’entrata nel campo sul poggio a sinistra.

Si nota la Chlora in fondo a destra della foto vicino ad un iperico; guardando lungo la strada si intravedono appena la cima e le foglie inferiori del tasso barbasso (ingrandire) e il ‘passello’ che devia sopra poggio.
Un altro esemplare fu presente per un paio d’anni passati sull’argine destro scendendo lungo la strada Sant’Anna, qualche decina di metri dopo la recinzione dell’uliveta sulla sinistra e qualche decina di metri prima del bivio per il P. Ponsino.
SU E GIU’ NEL TEMPO: uno sguardo nel futuro…
SI AGGIUNGONO FOTO DEL BARBASSO APPARSO DUE O TRE ANNI DOPO LA SUA TOTALE SCOMPARSA DALLA PASSEGGIATA (avvenuta circa nel 2017), PRATICAMENTE NELLO STESSO POSTO, scattate da Piero Pistoia.
SIAMO AL 3 FEBBRAIO 2019 e abbiamo scattato la seguente foto, scendendo verso il Ponsino a destra a metà argine:
CHI SA SE A PRIMAVERA-ESTATE DEL 2019 lo vedremo fiorito!
RIPORTIAMO ALTRE FOTO DI V. thapsus scattate intorno al 20 Aprile 2019 a seguire, scendendo verso il Ponsino sempre a destra sull’argine.
LE DUE SUCCESSIVE FOTO SONO STATE SCATTATE IL 13-05-2019 sullo stessa stessa pianta
La stessa pianta il 20 maggio 2019
Il 20-Giugno-2019, un mese dopo, il tasso precedente è ormai fiorito ed ha raggiunto almeno due metri di altezza come dalla foto successiva:
Mentre, tornati qualche giorno dopo il 20 maggio 2019, poco oltre il bivio per Il Ponsino sempre sulla sinistra della strada scendendo, l’erba qui è stata tagliata…. e la piantina che segue nata al bordo della strada è stata soppressa.

Vicino alla precedente rimangono, sotto strada, altre tre piantine che in estate speriamo di vederle invece fiorite, ma, prevedo, sarà improbabile; vedremo….
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Oggi, 24, giugno, 2019, subito dopo il Solstizio estivo, ho fotografato di nuovo le piantine del thapsus, davanti al P. Ponsino, sotto strada, due lontane si intravedono presso la quercia:
Le stesse due piantine che si intravedono vicine alla quercia precedenti, sono individuate nella foto scattata da Pier Francesco Bianchi il 27-06-2019
Seguono le foto che ho scattato sull’argine destro scendendo subito prima del Ponsino il 24- giugno-2019:
Nella precedente si intravede a destra il podere e lontano l’ingresso al podere.
Seguono ancora foto di Pier Francesco Bianchi del thapsus sull’argine e foto scattata dall’ingresso al podere, verso l’argine.
Si intravede il thapsus lontano sull’argine, e la casa e l’ingresso subito a sinistra.
Ancora una memoria dal futuro: siamo a giugno 2019
Chi volesse leggere questa breve memoria in pdf, cliccare sotto:
VERBASCUM thapsus,INTERVENTI MINIMALI E PROBLEMI PLANETARI – breve memoria
Altrimenti continuare a leggere:
VERBASCUM thapsus e la BIODIVERSITA’: breve memoria
PROPONGO UN PROCESSO MINIMALE PER LO PIU’ CULTURALE PER ARGINARE LA SCOMPARSA DI SPECIE SULLA SUPERFICIE DELLA TERRA
Intervento a mosaico in ogni zona, che favorirebbe anche la consapevolezza culturale del problema della estinzione delle specie e della Biodiversità (l’ONU attualmente ha valutato che otto milioni di specie sono a rischio)
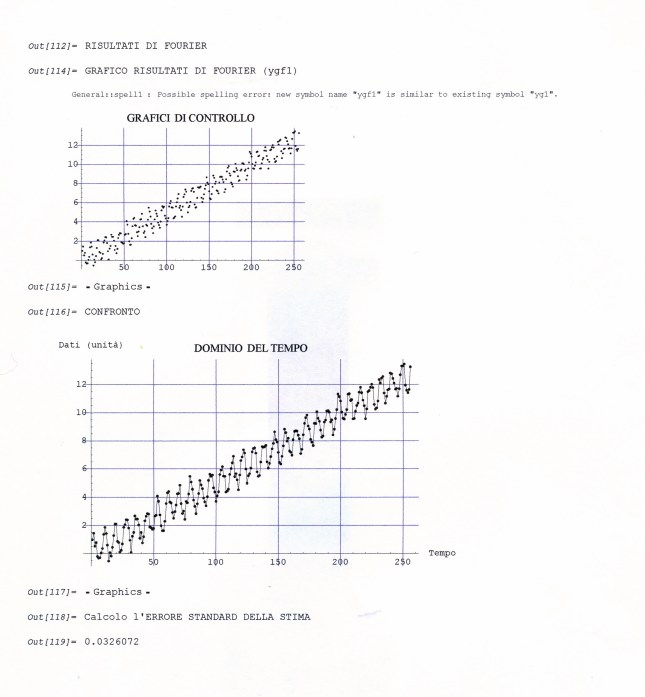
Noi abbiamo seguito per più di due anni un percorso floristico in una zona più periferica del paese (lungo la vicinale Sant’Anna di Pomarance), scansionando i suoi margini mensilmente. I processi ed i risultati di questo ‘diario’ sono riportati in sette posts nel Blog ‘ilsillabario2013’.
Due o tre anni fa apparve una piantina, unica in tutto il percorso, di Verbascum thapsus, a cui avevano tagliato l’alto butto fiorifero (si trovava sull’argine destro, scendendo lungo la vicinale Sant’Anna, vicino al viottolo del Podere ‘Il Ponsino’). Esistevano, invece, allora come oggi, altre specie del genere Verbascum (il sinuatum, il blattaria…)
Andammo ad avvertire le guardie comunali per salvarla dai periodici tagli dell’erba. Questo intervento permise alla piantina lo sviluppo di due altri butti fioriferi, che raggiunsero la maturazione dei loro semi.
Dopo anni è riapparsa oggi (grosso modo nello stesso posto), una fiorente piantina di thapsus, e, giorni dopo, sono apparse altre piantine nei dintorni.
Siamo allora tornati presso l’ufficio delle guardie comunali ad avvertire della loro presenza. Se l’avvertimento verrà accolto, si moltiplicherà esponenzialmente il numero di piantine di questa specie, insieme alle molteplicità di microrganismi ed organismi al contorno, utili per la reciproca sopravvivenza, in una zona dove il thapsus era completamente assente.
Dal Comune ci hanno informato che ultimamente il responsabile del taglio dell’erba in questa sezione di strada è l’abitante del podere Il Ponsino; interpellato il 25-05-2019, ci ha assicurato che la piantina tabellata verrà risparmiata.
Un piccolissimo gesto moltiplicato all’infinito prima o poi fa la differenza, come insegna l’analisi matematica (come la raccolta di una bottiglia di plastica abbandonata sul corso di un fiume, in un bosco …, o donare un tozzo di pane e formaggio, di vangelica memoria, ad uno che bussa alla tua porta…, o regalare una scatola di antibiotici ad una madre per il suo piccolo ammalato …, o sforzarsi di non utilizzare oggetti che scaricano in atmosfera concentrati di elementi che distruggono la protezione del pianeta, ed altri gesti minimali che al limite potrebbero davvero risolvere gli immensi problemi planetari, oltre naturalmente a maturare, in termini educativi, la consapevolezza morale verso i bisogni degli altri umani ed del pianeta).
pieropistoia
Le seguenti foto sono state scattate il primo settembre 2019 da Pier Francesco Bianchi dove si vede la precedenta piantina di V. tapsus in piena maturazione, in particolare quella grande sull’argine destro scendendo, subito prima dell’accesso al podere Ponsino; ma anche le altre tre salvate davanti all’accesso stesso e subito dopo sulla sinistra sono maturate.
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

Murex
LA COMPOSITA ACHILLEA millefolium
– continua la piena fioritura dell’Achillea millefolium, via del Poderino, davanti al cancello chiuso dello stadio con cartello in perallum (vedere foto) e davanti al P. San Vittore, prima della salita sulla vicinale Sant’Anna verso il Ponso insieme alle piante da giardino; ora ‘domina’ in altezza (vedere foto). Qualche piantina a sinistra sulla salita.
… ora ‘domina’ in altezza…
CONFRONTO DELLE FOGLIE DI ACHILLEA E FILIPENDULA
Dal 20-04-2019, al 25-05, vari anni dopo la fioritura dell’Achillea delle foto precedenti, sono state riprese altre foto ‘in crescita’ nel fossetto davanti allo stesso podere San Vittore:
LA BORRAGINACAEA BORRAGO officinalis
-Sta sparendo la Borrago officinalis (vedere foto); presente da Maggio nel prato subito sotto strada di via del Poderino, ora tagliato e lungo la vicinale Sant’Anna scendendo, a destra lungo l’argine dove esisteva prima il Tasso Barbasso; l’argine è stato da poco ripulito. Appare un residuo (presenza di un indicatore in peralluman) una decina di metri dopo il bivio per il P. Il Ponsino.
Della Filipendula praticamente è cessata la fioritura e si vedono molte foglie basali e qualche raro fiore (diffusa nel percorso), si notano ceppi di Antemis cotha, la Nigella damascena sta fruttificando (grosse capsule con ancora qualche fiore), ridotte le pervinche (davanti cartello per P. Mirto), la Verbena che appena è iniziata a fiorire (prima settimana), Ombrellifere, in particolare una specie, appena fiorite (10-6) diffuse nel percorso, in particolare all’inizio strada sterrata davanti al cartello per P. Mirto), e, ancora, Echium vulgare, le Campanule (diffuse), i finocchi selvatici (diffusi), i cardi (in particolare il Cardo dei lanaioli, Dipsacus fullonum, lungo la strada sterrata), la Cichoria entibo (diffusa velocemente), le Malve (diffuse), Composite che iniziano con un unico stelo breve rigido con grosso capolino e foglie lanceolate spesse e un po’ pelose e seghettate stanno crescendo (da classificare: vedere la classificazione di C. Moratti nel mese di settembre), le Potentille gialle (in cima al poggetto), le Plantago con le specie maior e minor (diffuse), l’infestante Inula viscosa, l’Artemisia con le specie absinthium officinalis. Il giorno 18-6 davanti al P. Sant’Anna lungo la vicinale a ridosso dell’argine si notano varie e fresche piantine anche fiorite della labiata Camedrio (Teucrium camedris), la scarpata non è stata ancora tagliata, lo sarà fra breve! Il 19-6, lungo il tratto Via dei Filosofi, inizia la crescita di un terzo Verbasco, con rosetta a foglie larghe e pelose che tendono ad ondulare al bordo (vedere dopo la classificazione). DA CONTINUARE.
LA COMPOSITA ANTEMIS chota

Fiore di Nigella damascena con fiori della Potentilla gialla (in uno dei quali si notano anche i sepali del calice)
IL PROBLEMA DELL’OMBRELLIFERA DI LUGLIO
…Ombrellifere (Umbelliferae, o Apiaceae) da poco fiorite…
Fusti eretti con steli non cavi (da controllare meglio), striati longitudinamente, leggermente spinati al tatto, sezione forse pentagonale (o triangolare?), 5 pedicelli fioriferi esterni più lunghi e 4 interni più brevi, forse uguali a due a due. Pianta ramificata di aspetto ‘delicato’ ed aperto. L’infiorescenza è composta da ombrelle di 9 peduncoli e da brevi ombrellette di una decina di fiori bianchi con alcuni piccoli petali (da precisarne numero e forma). La forma delle foglie è desumible dalle foto riportate. Per i frutti aspetteremo la maturazione. Oggi ( 18-6) sono maturati alcuni frutti, una decina o meno per ognuno dei peduncoli.
L’OMBRELLIFERA TORILIS arvensis

Da classificare! Piero Pistoia ipotizza che l’Ombrellifera del genere Tòrilis sembrerebbe probabile rispetto alle griglie disponibili: foglie pennato_divise; ombrelle convesse senza involucro a 4-12 raggi con peduncoli oltre 5 mm; fiori terminali a fusti e rami; frutta (acheni) ad aculei uncinati diffusi sui due semifrutti; forse la specie è Tòrilis arvensis.
Cinque peduncoli fioriferi dell’ombrella esterni più lunghi e quattro interni più brevi, forma di una foglia intermedia.
LA VERBENA officinalis
La foto che precede è una Verbena prima di fiorire (prima settimana)
La foto che segue è …..la Verbena che appena inizia a fiorire…(si intravedono Cardi)
–

Potentilla gialla (Potentilla reptans) con 5 petali e 10 sepali, dei quali 5 appaiono da sopra del fiore
LA POTENTILLA gialla
Fiore di N. damascena con fiori di Potentilla
L’ARTEMISIA absinthium
IL PROBLEMA DELLA COMPOSITA D’AGOSTO DA CLASSIFICARE


…Composite che iniziano con un unico stelo breve rigido con grosso capolino e foglie lanceolate spesse e un po’ pelose e seghettate….
….e, ancora, la Borraginacaea Echium vulgare (erba viperina)…


Non abbiamo incontrato ancora la Borraginacaea Anchusa
Seguono le foto del Cardo dei lanaioli (Dipsacus fullonum)

Le grandi foglie opposte, che si saldano alla base, formano una coppa che raccoglie una piccola riserva di acqua piovano o di rugiada condensata
——————————————–
SEGUONO LE FOTO DEL Camedrio
—————————————–
L’Iperico perforato
DIARIO FLORISTICO AGGIORNATO AD OGNI VISITA NEL CORSO DEL MESE DI LUGLIO 2015
Tutte le foto, se non sono nominati altri autori, sono di Piero Pistoia
Le Foto sotto della Pianticella X in fioritura in Luglio sono proposte per fare le osservazioni (sempre con ipotesi) insieme ai lettori, se ci sono, altrimenti fra noi, per classificarla. La sua stazione floristica si trova a destra, scendendo lungo la Vicinale di S. Anna, prima di una decina di metri dal bivio per il Ponsino. Fa vistosa presenza (oggi 22-luglio) sull’argine sinistro al bordo della ‘recinzione con riparo’ dell’uliveta, con altezze max fino a quasi 2 metri. Altra nuova piantina è la Silene, piccoli steli spesso affastellati, in Luglio in fiore, che crescono insieme all’Achillea ‘cartellata’ in Giugno, oggi con semi, presso il cancello chiuso da tempo del campo sportivo in via del Poderino. Ne vedremo le caratteristiche classificative. Rimangono ancora alcune pianticelle di Verbascum Blattaria sul poggio dopo il P. Ponso e davanti al P. S. Domenico (controllare le caratteristiche di classificazione); molto diffusa è ancora la Cicoria, l’altro Verbasco con foglie pelose larghe ondulate alla base (vedere foto rosetta di base) e con caule ramoso (quasi, a colpo d’occhio, a candelabro ebreo spaziale), ancora non nominato, ma presente anche a giugno, come vedremo. Il Verbascum tapsus, cartellato e nominato a giugno, si si sta spengendo con la siccità, insieme ad altre pianticelle di giugno morte o sofferenti (Plantago minor, il Camedrio, la Potentilla, l’Iperico, la Nigella, l’ombrellifera ‘Terentis’, la Chlora, il Camedrio che nel contempo era apparso anche sull’argine presso il bivio per il P. San Pietro,…); una pioggia a fine luglio potrebbe migliorare la situazione. In luglio una nuova Ombrellifera da studiare. Vedremo. Una nuova Asteracea, che somiglia al fiordaliso, è apparsa in luglio ed è visibile, scendendo lungo la sterrata per qualche centinaio di metri dopo un primo cartello per il P. Il Mirto, posto su una quercia a sinistra subito dopo P. Poggio Bartolino, distante 5-6 metri dal tasso barbasso ormai seccato sulla sinistra, ad una decina di metri dal ‘passello’ verso l’argine sempre a sinistra per il poggio; ancora da osservare e studiare. In giugno era apparsa sull’argine a sinistra una pianticella analoga subito prima del cancello del P. Poggio Bianco, al bivio per P. Il Mirto. Al podere Ponsino è apparsa improvvisa la pianta-fiore dell’Agave da ammirare!
ALTHEA cannabina
ALTHEA cannabina
IL PROBLEMA DI UNA MALVACEA IN LUGLIO: L’ANTHEA cannabina

Tavola delle caratteristiche da noi osservate della Piantina X: le altezze delle piantine raggiungono oltre 1.5 metri; foglie alterne palminervie (da un centro alla periferia), sopra più lucide, stipolate; le foglie inferiori sono sub-orbicolari, le superiori 1-2 pennato-partite (polimorfismo fogliare); fiori con calicetto esterno più piccolo; calice interno più grande i cui sepali, sembra, andranno a costituire la capsula dei semi; i 5 petali, piuttosto larghi, tendenzialmente separati (corolla dialipetala), con unghia breve rispetto al lembo terminante piatto e crenato, sono alternanti alle punte del calice; nella capsula del seme, i semi singoli sono ‘agganciati’ a ‘ciambella (fig. 1789) Da aggiungere la descrizione dei colori del fiore, degli stami e dell’ovario.
DIGRESSIONE SULLE FOGLIE PALMINERVIE
La foglia si dice palmata o palminervia quando ha la forma di una mano a dita aperte e le nervature sono disposte come le dita a partire da un punto che può essere l’inserzione del picciolo. Le palminervie si dicono incise o lobate secondo la profondità e ampiezza delle divisioni.
Palmato-fise: incise fino a metà della distanza margine picciolo;
Palmato-partite :incise fino a 3/4;
Palmato-sette: incise fino all’inserzione del picciolo;
Palmato-lobate: sono foglie con bordi arrotondati, allargate alla base, incide fino a metà.
VEDERE GLI SCHIZZI numerati sotto NEL TESTO: Eduard Thommen “Atlas de poche de la flore suisse”, 1961, Editions Birkhauser Bale. Ringraziamo l’autore e l’editore se ci permettono di vederli in questo blog di frontiera fra scolastico ed extra scolastico, dove, senza fini di lucro, si tentano nuove vie di ‘costruire’ conoscenza, almeno nella nostra intenzione.
1789 Malva alcea con struttura a ‘ciambella’, come tutte le Malvaceae, dei semi all’interno della capsula.
1790 Malva moschata.
1991 Malva silvestris.
L’ESPERTO, L’ERBORISTA ANGELO BIANCHI, HA SUGGERITO IL NOME PROBABILE DELLA FAMIGLIA E FORSE DEL GENERE:
Famiglia: MALVACEAE
Genere: MALVA, ma vedremo meglio
I DUE DISEGNI CHE SEGUONO si possono vedere usando il numero nel testo: Pietro Zangheri “Flora Italica II”, pag. 77, CEDAM-PADOVA.
Questo blog è senza alcun fine di lucro, e tenta di sperimentare vie anche nuove per ‘costruire’ conoscenza.
2808: Anthaea cannabina (Malva canapina); calicetto con 7 punte e calice con 5 punte
2806: foglia medio-superiore della Althaea cannabina che ha foglie verdi lucide sopra e più pallide sotto, le inferiori sono palmato-partite a 5 lacinie, le medie e superiori palmato-sette (2806), antere rosso porporina; cocche (mericarpi glabr i) rugose sul dorso.
IL DISEGNO dell’ Altea cannabina è visibile nel TESTO: Sandro Pignatti “Flora d’Italia vol. II”, Edagricole , alla trattazione della FAM. 90: Malvaceae (pag. 92).
Si lascia al lettore interessato l’onere di confrontare le caratteristiche osservate riportate nelle nostre foto e/o rilevate da lui stesso sul campo direttamente, con quelle riportate nei testi di filtro da noi nominati od altri a sua disposizione, onde ipotizzare una plausibile specie per la piantina X.
Foto delle piantine X; sullo sfondo il sentiero per il Ponsino
——————————————————–
L’Ombrellifera di luglio (da classificare)
 Foglie della Umbellifera di luglio; siamo in Attesa di fotografarne il seme
Foglie della Umbellifera di luglio; siamo in Attesa di fotografarne il seme
VERRA’ CLASSIFICA A SETTEMBRE DA CRISTINA
————————————————————-
SCROPHULARIACAEA VERBASCUM sinuatum
VERBASCO DIFFUSO IN LUGLIO
(vedere foto precedente)
———————————————————————–
L’esperto botanico, l’Erborista Angelo Bianchi ha classificato la nuova asteracea di luglio, prima individuata e segnata lungo il percorso e sotto fotografata, come Centaurea jacea (detta fiordaliso stoppione). La seguiremo anche in agosto e ne vedremo le caratteristiche. Sembra ci siano due sottospecie della C. jacea secondo la larghezza delle foglie: l’una max 1 mm e l’altra 6-7 mm (Cristina).

Centaurea jàcea (fiordaliso stoppione). Esisterebbero (Cristina) almeno due subspecie in funzione di foglie strette e larghe.
________________________________________________________________________
INTERMEZZO SULLA C. jacaea
Il 18-0tt. spedii a Cristina Anna una e-mail di cui trascrivo una parte riguardante la jacea:
<<…ti allego qualche foto di due piantine, raccolte a distanza di pochi dm, che ho colto nella Macchia di Monterufoli ieri; probabilmente si tratta di una Composita e forse del genere Centauraea; per la specie si tratta di un’unica specie (per es., C. jacaea) o di due specie diverse? L’una ha foglie a lacinie (largh. max circa 1 mm); l’altra ha foglie lanceolate ruvide al tatto e leggermente spatolate (Largh. max 6-7 mm); circa uguali in lunghezza; forse stesso stadio di fioritura…>>. Ecco le foto:
Fine intermezzo
_________________________________________________________________________
IL PERCORSO E LE PIANTINE DI AGOSTO
ABBIAMO TENTATO GIA’ DI DESCRIVERE IL PERCORSO BOTANICO DI AGOSTO, MA CON SORPRESA LO SCRITTO E’ SCOMPARSO PER DUE VOLTE: PROVIAMO ANCORA UNA VOLTA!
In agosto si sono alternate settimane molto piovose ed altre di un caldo afoso. Questo ha permesso la ricrescita di alcune piantine scomparse o regredite in luglio e rifiorite a fine Agosto (per es., l’Iperico, la Plantago, alcune composite, ecc.). Altre sono esplose diffondendosi ovunque come la Verbena, i Finocchi, il Verbascum sinuatum. E’ fiorita un’altra Centaurea jacea verso il poggetto del Ponso, a sinistra salendo dal P. San Vittore. Lungo la strada dei Filosofi sta diffondendosi la Scrofulariacaea Linaria vulgare di agosto. (Vedere foto sotto). Da studiarne i particolari.
La Scrofulariacaea Linaria vulgare di Agosto
La Scrofulariacaea Linaria
————————————————–
Davanti al P. San Vittore è presente un denso cespuglio spinoso forse di Cirsium, una nuova pianticella di agosto (vedere foto sotto). Da studiarne i particolari.
L’Achillea millefolium di San Vittore ha i semi. mentre quella di via del Poderino, presso il cancello dello stadio, è stata tagliata insieme alla Silene e il cartello in peralluman è sparito! Ci auguriamo che non venga gettato in discarica, ma che serva al suo possessore per attivare la sua curiosità per questo mondo povero della botanica spontanea. Sarebbe la sua migliore fine, perchè è lo scopo per cui è stato costruito!
PROBLEMA DEL CIRSIUM DI AGOSTO

L’Astreacaea Cirsium (?) del P. San Vittore; ipotesi sul genere e sulla specie (TT di Popper) di P. Pistoia: pannonicum o monspessulanum; da controllare (EE di Popper). Si confronti intanto con i disegni numerati sotto in E. Thommen (opera citata).
Disegnivisibili in Eduard Thommen (opera citata)
2835 – Cirsium monspessulanum
2836 – Cirsium pannonicum
In effetti le foglie non sono decorrenti al fusto e la ‘radice’ stolonica con semplici radicette! Forse l’ìpotesi non è corroborata! Vedremo tentativi successivi di ipotesi.
E’ stato interpellato il nostro erborista Angelo Bianchi, che ha avvallato l’ipotesi del genere (Cirsium) ed ha proposto come specie, C. arvense.
L’involucro a ‘bicchiere’, le foglie pennatofide, la presenza di una infiorescenza aspetti notabili nei disegni forse potrebbero suggerire che la nostra pianticella possa essere una varietà del C. arvense. Una investigazione su un fiore singolo (presenza di 5 lacinie nella corolla), chiarirebbe intanto la questione del genere. Si apre una discussione.
DISCUSSIONE APERTA SULLA NOSTRA SPECIE DEL Cirsium
Piero Pistoia – In effetti, specialmente la parte alta della pianticella. che ad occhio presenta lunghi steli dei capolini, terminali e solitari, e piccole e regolari foglie quasi intere (più oblungo-lanceolate) leggermente spinose, praticamente senza infiorescenze…, rendono il nostro Cirsium , almeno in apparenza, più elegante e meno selvatico del C. arvense di riferimento (vedere disegni); ciò si conferma anche osservando lo stesso involucro non a forma di bicchiere di vino (tozzo a pareti verticali o quasi), ma piccolo e delicatamente allungato mentre si restringe verso l’alto. Forse si può concludere che il nostro Cirsium arvense sia una varietà della specie standard. Insomma la nostra pianticella ha svariate caratteristiche appartenenti alla zona di intersezione fra diverse specie di Cirsium e ciò mi porterebbe a formulare un’ipotesi fortemente azzardata, ma per questo profondamente scientifica (alta falsificabilità), cioè che si tratti di una nuova varietà.
Altri disegni da controllare in:
Eduard Thommen (opera citata)
2833 – Cirsium arvense
2834 – Cirsium palustre
…. e in Pietro Zangheri (opera citata)
5469 – Cirsium arvense; fiore singolo con ovario e pappo
5470 – Cirsium arvense; cima fiorita e foglie chiaramente pennatofide (incise fino a metà distanza bordo-asse
————————————————-
CONFRONTARE I DISEGNI PRECEDENTI CON LE FOTO DEL CIRSIUM CHE SEGUONO (ESEGUITE DA P. PISTOIA)

Foto delle blattee dell’involucro (dim. L. da 2-3 a 10-11) del Cirsium; la punta scura sembra che continui in un dorsale nera. Alla lente danno l’impressione visiva di un aglio stretto visto dal dorso.
INTANTO SIAMO ARRIVATI AI PRIMI DI SETTEMBRE.
Gli ultimi temporali hanno modificato qualcosa nel percorso. Fra il P. Sant’Anna e P. San Vittore, in particolare presso il ‘pelago’ del P. San Vittore è esplosa la comunità della pianticella che abbiamo classificato come Centaurea jacea, che fa bella vista al bordo del piccolo laghetto del podere.
Si stanno diffondendo rapidamente le gialle Linarie, mentre sta regredendo la fioritura del Verbasco a ‘candelabro’ e l’altra Scrofulariacaea Echium. Si iniziano a vedere i piccoli capolini gialli della Composita, già diffusa, Inula viscosa. Altre piccole composite hanno invaso il percorso da classificare. Sporadicamente è ricresciuto qualche Verbascum blattaria con un solo fiore e qualche Iperico giallo stellato; occhieggia ancora qualche fiore di Cicoria insieme alle piante grigiastre con i suoi semi. L’Achillea, dove era rimasta, mostra i suoi frutti nerastri sporchi; si nota ancora qualche rara capsula di Nigella damascena. La piantina spinosa che abbiamo riferita al genere Cirsium si è estesa per qualche metro quadro dal bordo strada verso il campo proprio davanti al P. San Vittore e sta ancora fiorendo in attesa di un nostro studio più approfondito sul seme ed il pappo ed altro. Al poggio Il Ponso, verso il campo, si notano fioriture abbondanti di Calamintha nepeta (armai diffusa ovunque) e qualche pianta rimasta da tempo di Salvia selvatica. Qua e là, dove erano, si nota ancora qualche Verbascum Blattaria ormai con i semi. Diffusa è anche la Verbena officinalis, il finocchio e anche l’Althea, nello stesso posto qualcuna ancora in fiore. Continua la diffusione dell’Ombrellifera di agosto che ancora dobbiamo classificare, perché nessuno fin’ora si impegnato a farlo.
————————————————————
INIZIO PROPOSTA PER UNA TENDENZA A CAMBIARE ‘POLITICA’ NEL POST
Chi ha scritto fin’ora sul post, cercando di alimentare le discussioni ed ordinando le diverse informazioni e foto, ha problemi familiari e di tempo, per cui ha scambiato le seguenti email con la co-curatrice Cristina Anna Moratti, cercando di modificare la politica del post in corso.
PIERO P.-CR1-> contenuto inviato a Cristina per e-mail (DA RIPORTARE E CONTINUARE)
LA CLASSIFICAZIONE DELLA OMBRELLIFERA DI LUGLIO AGOSTO
Cristina Moratti, interpellata oggi (11-sett;11.30; oggetto: lavoro da svolgere sul percorso botanico), ha formulato un’ipotesi sull’Ombrellifera (Apiacea) di Luglio-Agosto ancora da classificare. Dovrebbe trattarsi di una Daucus carota non per le sue foglie molto variabili in questa specie*, ma per la presenza dei piccoli ‘fiorellini’ scuri al centro dell’infiorescenza, perché, afferma Cristina, ciò è tipico della carota selvatica, anzi è uno dei pochi segni che portano alla sua identificazione**. La pianta comunque, se stropicciata, profuma di carota. L’altra Asteracea con infiorescenza gialla, fotografata e descritta a giugno, ancora presente anche se rara, ma non ancora classificata, afferma ancora Cristina, potrebbe essere un Asteriscus spinosus (Pallenis spinosa).
CR-PIERO1 -> contenuto inviato da Cristina a Piero in risposta alla e-mail precedente (PIERO-CR1) (DA RIPORTARE E CONTINUARE)
*In effetti confrontare le foto delle foglie dell’Umbellifera nel ‘diario’ di luglio con la Carota selvatica riportata sui testi di riferimento….
**Altri segni potrebbero essere la radice a fittone anche se non molto sviluppata, la contrazione dell’ombrella a nido di uccello, il numero dei raggi dell’ombrella e dei fiori per ogni raggio, la forma del seme, la forma delle stesse foglie ed altro. Vedere per es., gli schemi da riprendere dai testi di riferimento (potrebbero essere aggiunti). Vedere anche le tre foto successive della D. carota un po’ appassita fotografata oggi.

D. carota: pianta terminale; rami, foglie e infiorescenze mature (ombrella completamente contratta). Sarebbe interessante riuscire a fare foto dei semi chiare. In molti casi la forma del seme è probabilmente l’elemento più decisivo nella classificazione.
Ci sono comunque oggi a settembre, altre composite ‘povere’, alcune molto diffuse, diverse dall’Inula viscosa ed altro da classificare! (vedere foto sotto). Basta seguire il percorso, osservare, formulare le ipotesi e seguire i processi di controllo.
PIERO-CR2 -> Su alcune foto seguenti aggiunte a settembre (il procedere descritto dall’aforisma sul gatto) DA RIPORTARE E CONTINUARE
LE SUCCESSIVE SETTE FOTO RIGUARDANO UNA DELLE PIANTINE PIU’ DIFFUSE NEL PERCORSO
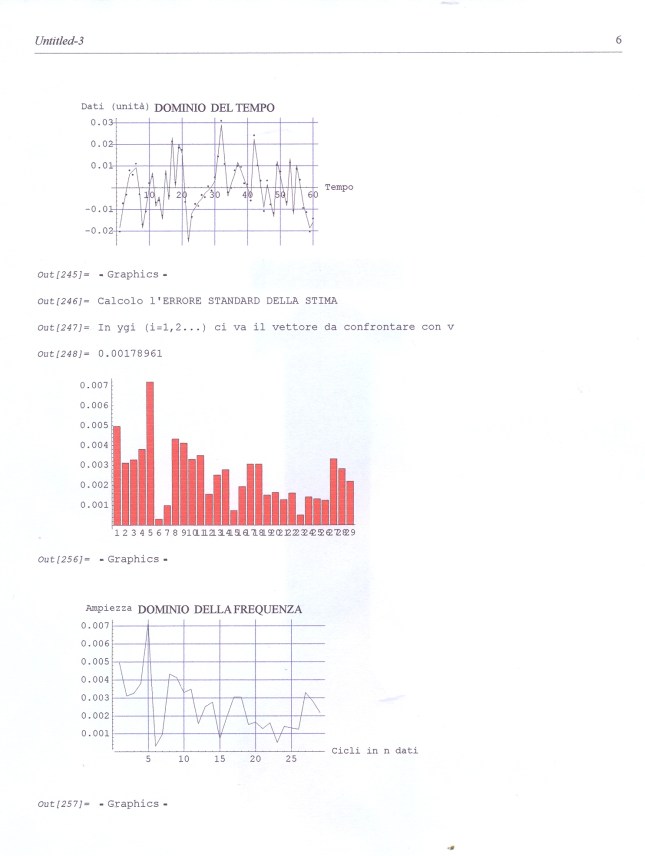
(La prima foto è di Cristina Anna Moratti)
———————————————–
Uguale alla precedente
CR-PIERO2 -> e-mail sulle precedenti foto ed altre in settembre (DA RIPORTARE E CONTINUARE)
PIERO-CR3-> e-mail sulla sintesi sulla proposta, motivata anche da ragioni teoriche, per il cambiamento di politica sul post. (DA RIPORTARE E CONTINUARE)
TERMINE DELLA PROPOSTA PER UNA TENDENZA A CAMBIARE ‘POLITICA’ NEL POST
——————————————————————-
ANCORA DA ORGANIZZARE LE FOTO DELLE E_MAIL DI CRISTINA
RIFLESSIONI CRITICHE E PERCORSI PER ACQUISIRE DIMESTICHEZZA EMPATIA ED EINFUNLUNG SULLE SPECIE PROPOSTE DA CRISTINA MORATTI
Cerchiamo di costruire le idee di questi ‘oggetti’ nella mente a partire dalle ipotesi di Cristina
Osserviamo intanto da vicino l’Inula viscosa o Cupularia viscosa (ceppica; da noi detta ceppita)
Da notare le cime a pannocchia densa di fiori gialli

Pianta perenne. suffruticosa con fusto eretto, legnoso alla base con foglie che si riducono salendo lungo il caule; capolini (1-1.5 cm) numerosi con pannocchia ricca.

Foglie più o meno vischiose e oblungo-lanceolate debolmente crenate sessili o semi-abbraccianti; fiori con una decina di ‘petali’ al capolino (cioè petali dei fiori periferici esterni raggianti a linguette lunghe rispetto all’involucro – da descrivere e del quale ora manca la foto); se strofinata emette un odore aromatico poco gradevole; da continuare (aggiungere qualche disegno schematico).
SCHEMI DELL’Inula viscosa (seme e pianta) visibile nel TESTO DI P. Zangheri (Cedam; opera citata) e NEL TESTO DI S. PIGNATTI (Edagricole, opera citata)
Osserviamo anche la Composita gialla con fiori giallo-dorati spesso associata all’Inula che presenta molti più ‘petali’ intorno al capolino, con foglie quasi della stessa forma forse più minute e più rugose. Fusto senza rosetta basale; le foglie cauline tendono ad abbracciare il fusto con due orecchiette più o meno sporgenti (da controllare). Pianta lanoso-biancastra o mollemente tomentosa; radice non fittosa. L’ipotesi di Cristina Moratti è “Pulicaria dysenterica“, detta Incensaria comune.
Segue la bella foto di Cristina Anna Moratti del capolino della P. dysenterica
VISIONARE LA Pulicaria dysenterica (5124) NELL TESTO DI P. ZANGHERI (Cedam, opera citata)
Pulicaria dysenterica
——————————————————-
Cristina Moratti ha classificato la piantina con infiorescenza a ‘bruco scorpioide’ come Heliantus europeus.
Eliotropio, Erba porraia; si incontra nel tratto mediano del percorso corrispondente a via dei Filosofi, scendendo sulla destra
Visionare i disegni schematici della pianticella precedente nei testi di P. Zangheri ed S. Pignatti (opera citata)
SI TRATTA di Borraginacea cenerino pubescente, a fusti eretti fino a 40 cm; infiorescenza scorpioide densa; fiore a calice partito, corolla imbutiforme bianca a cinque lobi; fiori sessili; acheni rugosi.
SEGUONO ALTRE FOTO DELL’ELIOTROPIO
Heliantus europeus

SEGUE ANCHE LA BELLA FOTO DI CRISTINA ANNA MORATTI DELLA BORRAGINACEA DEL GENERE HELIANTUS, SPECIE H. europeum ESEGUITA NEL PERCORSO A SETTEMBRE (particolare dell’infiorescenza).
———————————————————
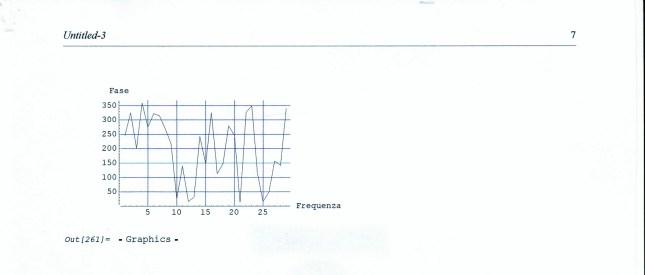
QUI L’OBBIETTIVO CONYZA o ERIGERON?
CONYZA o ERGERON?
SEMPRE DI CRISTINA sono le due foto successive della Composita molto diffusa da lei nominata Erigeron bonariensis
 Pianta alta con fiori, frutti e pappi. Penso che i fiori gialli non siano dati rilevanti (non appaiono mai in altre analoghe foto e neppure negli incontri (?) sul percorso).
Pianta alta con fiori, frutti e pappi. Penso che i fiori gialli non siano dati rilevanti (non appaiono mai in altre analoghe foto e neppure negli incontri (?) sul percorso).
_______________________________
COMMENTO DEL COORDINATORE Piero Pistoia (NDC)
Segue una foto di P. Pistoia di una specie dell’Erigeron (?) ripresa nel percorso: caule terminale con infiorescenza a pannocchia (?), fiore, frutto, foglia di base e foglia caulina. Altezze involucro 5 mm; max sezione involucro 3 mm; altezza fiore sopra involucro 1 mm.
Foto di una specie dell’Erigeron (affine al genere Aster e al genere Conyza) ripresa nel nostro percorso: caule terminale con infiorescenza a pannocchia (?) di numerossimi fiori, frutti bianco-piumosi, foglia di base e foglia caulina. Altezze involucro 5 mm; max sezione involucro 3 mm; altezza fiore sopra involucro 1 mm, spessore capolino 4-5 mm.
Foglie inferiori lanceolate con qualche seghettatura verso l’alto; divengono più piccole, sottili e strette a salire.
Erigeron è composta dalle parole greche er e géron, primavera e vecchio, forse ad indicare la rapida perdita delle corolle dei fiori e delle ligule del capolino quando ci sono e il precoce apparire al loro posto delle piumosità bianche dei pappi con i quali terminano i frutti; i capolini giallini più chiari al contorno, diventano in breve ciuffi candidi. Vedere foto. Man mano che si sale lungo la pannocchia aumentano i fiori trasformati in frutti; nella parte inferiore si notano ancora i fiori giallini del piccolo capolino. Il talamo sembra convesso.
VISIONARE i disegni schematici della Composita del genere Erigeron (da E. Thommen, (edit. Birkhauser Bale), opera citata) a partire dall’E. acer e lo schema di E. canadensis (2653 del testo sempre di Thommen)
Dall’osservare attentamente le foto, le piantine sul campo, partendo dall’ipotesi in prima istanza (Erigeron bonariensis), con i nostri testi di riferimento forse siamo in grado di formulare un’ipotesi di classificazione in seconda istanza, anche se abbastanza vicina alla prima.
- Altezza fusto 1-6 dm, striato (sezione diversa dalla circolare) con peli addensati che ha radice forse a fittone e termina in una pannocchia i cui ‘rami’ a tendenza corimbosa densi di fiori sono ‘rivolti’ verso il caule accentuando la forma a pannocchia della cima.
- Foglie inferiori lineari lanceolate, uninervie (un solo percorso centrale di alimentazione, una sola nervatura centrale) un po’ pelose; le superiori lineari strette.
- Capolini diametro 5 mm, con involucro (altezza circa 5 mm, max larghezza 2-3 mm) formato da squame in due serie. Altezza fiori sopra l’involucro 1 mm.
- Fiori periferici tubolari attinomorfi (alta simmetria), con 3-4 denti; assenza di ligule.
Seguono disegni schematici di riferimento per il raccontino precedente ripresi dai testi.
 FIORI ATTINOMORFI CIOE’ SIMMETRICI
FIORI ATTINOMORFI CIOE’ SIMMETRICI
Ipotesi in seconda istanza Conyza bonariensis (=Erigeron linifolius (foglie come quelle del lino), Erigeron crispus)
Saremmo onorati e soddisfatti comunque se un lettore interessato attivasse una propria argomentazione critica o una analisi personale dei dati forniti e di quelli da lui stesso recuperati da sue foto, da visite sul campo o dai nostri testi o da altri, o comunque dalle conoscenze a sua disposizione…., onde tentare di falsificare le ipotesi da noi proposte. In questo consiste il processo scientifico e in particolare l’obbiettivo più importante di questo blog! ed è questo il significato di “lavorare insieme per costruire conoscenza”
La piantina che appare nella foto dietro la bonariensis è in effetti un arbusto che Cristina ha classificato come Cornus sanguinaea, che sta per fiorire in questo autunno di nuovo (era fiorito anche a primavera) dopo svariate rasature.
FINE COMMENTO DEL COORDINATORE
Le due foto seguenti sono della composita ancora da classificare di Luglio-Agosto: Cristina Anna l’attribuisce alla specie “Asteriscus spinosus (Pallenis spinosa). Da commentare più in profondità (vedere in settembre)
DA OSSERVARE ANCHE LE FOTO DELLA SEGUENTE COMPOSITA ANCORA DA CLASSIFICARE ASSOCIATA ALL’INULA E ALLA PULICARIA
(Presso il poggetto del Ponso)

Fusto eretto (H fino a 60-70 cm). Foglie sessili diminuiscono in dimensioni procedendo verso l’alto; la forma fogliare, che ‘pensata intera’ avrebbe forma sub-ovale, varia da pennato setta vicino al caule a pennato fisa o seghettata.
Cristina Anna Moratti ha guardato le precedenti foto dell’Asteracaea da classificare; durante una sua visita al percorso in settembre, ha eseguito, sempre della stessa specie, anche le due belle foto dal vivo relative all’infiorescenza con capolini e della foglia che seguono e le ha classificate in prima istanza come appartenenti a Senecio jacobaea (Jacobaea vulgaris).
DA SINISTRA A DESTRA SEGUONO LE FOTO DI TRE CAPOLINI A CONFRONTO APPARTENENTI RISPETTIVAMENTE ALLE SPECIE CLASSIFICATE DELLA LINULA, DEL SENECIO E DELLA PULICARIA

Da notare i capolini di Linula che ha fiori mediamente più piccoli delle altre due specie. Simile è il numero delle ‘ligule’ del capolino (poco più di 10) nelle prime due specie; molto più alto nella terza, più raggiate e stellari.
SEGUE LA FOTO DELLE FOGLIE RIFERIBILI RISPETTIVAMENTE ALLE TRE PIANTINE A CUI SI FA RIFERIMENTO NELLA FOTO CHE PRECEDE
————————————————–
Durante la stessa visita Cristina Anna ha fotografato anche un’altra piantina di Asteracaea (le due foto dal vivo di un capolino e del gruppo di piantine) che ha classificato in prima istanza come appartenenti alla specie Cota tinctoria (Camomilla dei tintori). Manca il riferimento alla zona del ritrovamento, perchè non è diffusa come altre.
P. Pistoia ha eseguito la seguente foto delle foglie della Cota (uno dei pochi esemplari del percorso a settembre) raccolte nel tratto di Via dei Filosofi, scendendo sulla destra, a pochi metri dal bivio con la vicinale S. Anna
———————————————————-
LA NUOVA COMPOSITA DI FINE SETTEMBRE
Foto di piantina osservata lungo la vicinale Sant’Anna scendendo, sotto il grosso cipresso sulla sinistra all’ingresso del podere vecchio e proseguendo a sinistra, davanti al casolare nuovo dello stesso nome. Altre piantine si rinvengono oltre Poggio Bartolino sulla sterrata per Poggio Bianco. E’ stata raccolta e trasportata divenendo un po’ appassita.
Seguiranno foto dal vivo
Da osservare il fiore terminale sembra senza ligule o non ancora aperto.

Caule eretto, liscio, ramoso per lo più in alto, capolino molto piccolo apicale bianco-giallino (1-1.5 mm al di sopra della ‘copertura’ esterna (involucro) allungata, alta circa 6 mm e larga max 2 mm).

Parte finale della piantina; foglie lisce, semplici, uninervie, lanceolate avvolgenti un caule liscio (decorrenti per qualche cm), più piccole e strette verso l’alto; la radice appare a fittone. Altezza max circa 50-60 cm. Qui si sono aperti i fiori. Fiori periferici con piccole ligule bianche che si aprono solo parzialmente all’esterno (rimangono, almeno per ora, un po’ a guisa di ‘corona’); max ampiezza fiore composto fino a circa 7-8 mm.

Rametto fiorito con piccole ligule bianche, ora sembrano più aperte, che contornano un piccolo interno giallino (diametro capolino 8 mm circa).
SEGUONO FOTO DAL VIVO
Parte superiore pianta
Cristina ha classificato la piantina come un’Asteracaea, appartenente al genere Symphiotrycum squamatum (=Aster squamatus), nome comune: Astro Autunnale.
Confrontando le foto e la loro descrizione e le caratteristiche dell’Aster Squamatus, si conclude che l’ipotesi è corroborata (nel senso popperiano di ‘temporaneamente verificata’).
Riassumiamo la descrizione: fusto eretto che inizia da una radice a fittone e termina in un ramoso corimbo aperto; foglie inferiori lisce, semplici, uninervie, lanceolate avvolgenti un caule liscio, decorrenti per qualche cm (la_max per lu=1x circa 8 cm), più piccole e strette acute verso l’alto; foglie sui rami fiorali (1×8 mm), involucro stretto conico_cilindrico allungato con squame a lesina da calzolai in varie serie, nere in punta (aggiungere foto involucro); fiori ligulati piccoli bianchicci; capolino circa 7-8 mm.
————————————————-
Il Symphyotricum squamatum a confronto con Conyza (=Erigeron) bonariensis spesso associati strettamente in tratti del percorso (verso Poggio Bianco, dopo il cartello rimasto del Verbascum tapsus seccato, ultimo scorcio del percorso).
Da notare la forma degli involucri del fiore
INSERIAMO QUI UN LINK con la crucifera Lepidium graminifolium, nuova rosetta di Cerithe, Aster linòserys ed altro
SIAMO IN PIENO OTTOBRE……
IL PROBLEMA DELLA CRUCIFERA DI OTTOBRE
Ecco la prima nuova piantina da classificare; ad occhio sembrerebbe una Crucifera; forse un Erysimum? Vedremo. Sta diffondendosi rapidamente; l’abbiamo raccolta presso il podere Ponsino, ma l’abbiamo notata anche in altri punti del percorso. Seguono foto dal vivo.
Dopo una periodo di riflessione la precedente Brassicacea (=Crucifera) presso il Ponsino viene classificata da Cristina Anna come Lepidium graminifolium e si apre la discussione; di questa piantina seguono anche le tre foto di Cristina… e…:
…e… altre tre di P. Pistoia:
——————————————–
MA ECCO UNA PIACEVOLE SORPRESA: il 9-ottobre Cristina Anna ha notato nuove e numerose rosette di base della ‘ghiandolosa’ Cerinthe proprio dove le piante di inizio estate già adulte furono distrutte dal trattore (oggi forse potranno arrivare a rilasciare i semi, col diminuire del lavoro dei campi). Seguono tre foto di Cristina:
———————————————————-
Sempre ai primi di ottobre sempre Cristina ha fotografato la Cariofillacea Dianthus carthusianorum nei dintorni del P. Ponso (da precisare)
…e il più diffuso Cyclamen hederifolium (per vedere la scheda tecnica di quest’ultimo scritta sempre da Cristina, cercare nel sito ‘La Carrozza del Gambini’) e …
e…. (per risolvere l’enigma dell’Alyssum), la nuova e interessante Composita Galatella (=Aster) linòsyris (Astro spillo d’oro); foto riprese sull’argine vicino Podere S. Anna.
IL PROBLEMA DELL’ALYSSUM E DELLA GALATELLA
Osservando attentamente le foto dell’Astro spillo d’oro e visitando le piantine sul campo è probabile che nel mese di giugno fosse falso il mio ricordo dell’Alyssum; in effetti quella piantina gialla che intravidi nel 2014 durante il footing è facile invece che fosse la linòsyris! Ecco risolto l’enigma dell’Alyssum trapiantato nel Neoautoctono!
Foto di P. Pistoia dell’Astro Spillo d’oro presa davanti al P. Sant’Anna. Oggi 19-ottobre l’Astro Spillo costeggia la strada verso il P. San Domenico dalla parte della vigna.
VISIONARE IN E. THOMMEN (op. cit.) SCHEMA DELLA
GALATELLA (=ASTER) lynòsiris
——————————————————
Segue ancora una ‘erbaccia di odore sgradevole’ ripresa sul poggetto del Ponso, cresciuta in settembre che sta estendendosi a macchia d’olio; da classificare.

La nostra co-autrice Cristina Anna l’ha fotografata (vedere sotto) e classificata come una Chenopodiacaea di genere Chenopodium e specie album (Farinaccio). Alcune foto sono da cambiare.

——————————————————
Davanti alla stazione dell’Althea, studiata in estate, da tempo rasata, prima del P. Ponsino, sono rifiorite alcune nuove cannabine. E’ ormai completamente diffusa la Linaria gialla, il finocchio da ‘castagne bollite’ e la Calamintha nepeta. Rimane anche qualche pianticella in fiore di Verbasco blattaria (una davanti al P. San Domenico) che forse perdurerà per tutto l’inverno e qualche nuova pianticella (rosette di base) del Verbasco sinuoso e della Malva iniziale; invece continua ad essere assente il Tasso barbasso. Rimangono alcune cime annerite ‘corimbose’ piene di semi della composita Achillea millefoglio e resti stecchiti scuri e capolini anneriti di Asteriscus spinosus verso il Ponso. Sono presenti e vistose tutte le altre Composite descritte (in particolare la Linula, il Selecio e la Pulicaria). Qua là riappare qualche fiore di Scabiosa e di Cicoria. Permane negli stessi posti la Centauraea jacea ancora in fiore e il Cirsium spinoso con rari capolini. Cristina a osservato le ultime foto della Centaurea Jacaea e pensa che si tratti di C. jacaea subsp angustifolia. Rare appaiono le piantine Labiate di Salvia selvatica e di Ombrellifere. Permane il cespuglio di Composite di Anthemis (=Cota) tinctoria vicino all’incrocio di Via dei Filosofi con la Vicinale di Sant’Anna e in altri punti a metà di Via dei Filosofi, di controversa classificazione in particolare sulle dimensioni dei capolini. Sempre scendendo a sinistra per Via dei Filosofi è riapparsa una piccola piantina in fiore di Iperico perforato. Al P. Bartolino, sotto strada, appare una distesa di grossi capolini gialli di Tupinambur (Helianthus tuberosus).
L’ARTEMISIA
All’incrocio Mazzolari-Poderino, sotto strada, una estesa stazione di Artemisia vulgaris (?) dopo svariate rasature sta ricrescendo; al margine (vicino al grosso ulivo) si notano alte piante fino a 2 o più metri con infiorescenze (da continuare e approfondire). Questa stazione è rimasta attiva, nonostante gli svariati tagli, per almeno 35 anni sempre diffusa fra l’attuale grosso ulivo sulla strada e le piante di sambuco ed oltre lungo un buon tratto di strada del Poderino, distesa sul versante che guarda lo stadio, al di là delle auto in sosta nello sterrato. Da una ricerca che feci a quel tempo mi ricordo che la classificai come A. vulgaris, che prenderemo come ipotesi iniziale). Ma come ebbe a scrivere il grande medico naturalista fisico vissuto in pieno 1700 Giovanni Antonio Scòpoli (testo riportato da S. Pignatti , Vol III, pag. 101, opera citata):
<<Felix ille, qui ex auctorum Artemisiis se feliciter exstricaverit>>,
che in italiano suona come: <<deve ritenersi contento l’auctor che riuscirà a disistricarsi nel classificare le Artemisie>> e parlava uno che se ne intendeva!
Comunque noi, non così qualificati, faremo un nostro tentativo nel trovare la strada e rimandiamo come sempre ai lettori interessati di farne altri.
SEGUONO FOTO DELL’ARTEMISIA (mancano esplicitamente foto dei piccoli capolini e degli involucri e forse Cristina sarebbe in grado di farle!)

RAMO FIORIFERO A PANNOCCHIA STRETTA DENSO DI FOGLIE 3-4 PENNATOSETTE SEMPLICE, LINEARI NON SEGHETTATE, SEMPRE PIU’ PICCOLE SALENDO LUNGO IL FUSTO.

DESCRIZIONE DELLA PIANTA – Fusti eretti rigati alti fino almeno a due metri, legnosi in basso con rami terminali fioriferi; foglie pennatosette, glabre e scure sopra e bianco-tomentose di sotto; le inferiori (circa 9 cm x 10 cm) con tre-quattro lacinie lineari poco dentate (quasi intere) per lato; verso l’alto tendono a diminuire di area; capolini quasi sessili, forse a coppa (1-1.5 x 3 mm) in pannocchia fogliosa stretta pendula; radici stoloniche superficiali. Odore debole e poco gradevole.
LO SCORCIO DI STRADA A SINISTRA INDIVIDUA L’INCROCIO FRA VIA DEL PODERINO CON VIA DON MAZZOLARI (quest’ultima indicata dalla freccia)
VISIONARE SCHEMI DELLA A. vulgaris IN S. PIGNATTI VOL III, PAG. 103, EDAGRICOLE E DA THOLMENN (op. cit.)
VISIONARE SCHEMI DELLA Artemisia. verlotorum (A. DEI FRATELLI VERLOT) IN S. PIGNATTI VOL III, PAG. 103, EDAGRICOLE E DA THOLMENN (op. cit.).
2754 A. vulgaris
2755 A. verlotorum
da E. THOMMEN “Atlas de poche de la flore suisse” Editions Birkhauser Bale
RAPPORTO PROTOCOLLO-SPERIMENTALE /IPOTESI NEL NOSTRO CASO (da chiarire)
A. vulgaris differisce da A. verlotorum solo per alcuni aspetti: quelli ‘sperimentati’ – vedere foto – sono 1) la radice di A. verlotorum è stolonica; 2) le sue foglie sono tendenzialmente intere e scarsamente seghettate; 3) il suo involucro appare forse leggermente più corto tondeggiante, ma non ovoidale; la sua pannocchia è forse più stretta. L’aspetto di confronto incerto è il profumo che nell’esperimento (pianta stropicciata ed annusata) è assente o sgradevole.
CONCLUSIONI
La mia ipotesi proposta all’inizio ‘risulterebbe’ falsificata; è preferibile l’ipotesi che la piantina sia una Composita il cui genere sia Artemisia e la cui specie sia A. verlotorum (ipotesi corroborata). L’efficacia delle nuove ipotesi non obbediscono a nessun trucco se non quello di contenere più ‘elementi di verità’ di quelli delle ipotesi precedenti rispetto a un quadro di riferimento.
Nel mondo complesso, sosteneva K. Popper, se leggiamo fra le righe, ogni ipotesi è da ritenere falsa; per procedere nella conoscenza è necessario, se corroborata, tentare di falsificarla con ogni mezzo toccando ‘il reale’, qualsiasi cosa voglia significare, cioè ‘sbucciando la cipolla’ del territorio complesso in studio, sempre più in profondità.
—————————————-
ECCO LE FOTO RIPRESE IL 18 OTTOBRE
——————————————————

E’ rinata l’Erba Querciola (Camedrio; Teucrium camedris) sull’argine del P. Sant’Anna e presso la deviazione per il P. S. Pietro, dove appaiono anche tracce delle estive piantine con semi anneriti.

Erba Querciola (Camedrio); si intravedono vecchie piantine con semi sul calcare conchigliare del Pliocene medio dell’argine subito dopo il bivio per il P. San Pietro
————————————————–

Rametti di Ulmus campestris sopra rosette nel fossetto di Filipendula exapetala presente in ottobre davanti all’argine del P. Santa’anna.

Rosette di filipendula nel fossetto al di là della strada davanti all’argine del P. Sant’Anna, sotto gli aceri.
Rosette basali di Achillea millefolium sono ora rinate abbondanti nel fossetto lungo strada al Podere San Vittore, salendo a sinistra, proprio sotto i corimbi delle piante precedenti già rammentati, maturati durante l’estate ormai rinsecchiti ed anneriti, ma ancora presenti a sovrastare quelle del giardino. Seguiranno foto.

Rosette di base di A. millefolium nel fossetto sotto l’argine del P. San Vittore nate dai semi delle poche piantine estive sovrastanti descritte in luglio, che ancora esistono rinsecchite e con corimbi anneriti.
L’argine del P. San Vittore su cui esistevano in luglio le achillee in fiore, ricresciute in rosette nel fossetto alla base, oggi in Ottobre. Ingrandendo si nota ancora qualche ‘corimbo’ rinsecchito di Achillea. La strada sale sul poggetto del Ponso.
————————————————-

Si tratta di una Olivacaea: Ligustrum vulgare, classificato da Cristina, a foglie lanceolate ‘tenere e lisce ‘e semi-caduche davanti al P. San Domenico con bacche nere mature. Avevamo proposto l’ipotesi del Lillatro su ‘l’idea’ sbagliata che avevamo di esso!
Il Ligustro qui davanti al P. San Domenico è associato ad altre piante della macchia mediterranea (Pistacea lentiscus, Ulmus campestris, Quercus ilex, l’Alaterno, il Viburno, …). Questo fitto ‘arbusteto’ è anche intrecciato con la Lianacea spinosa Smilax aspera (Roghetta-stracciabrache) della quale Cristina a fine ottobre ha notato una seconda vistosa fioritura, invece di <<mostrare i grappoli con le sue belle bacche lucide>> come avrebbe dovuto. La S. aspera è ricordata in paleo-botanica perché, insieme ad altre piante, (per es., l’Alloro, la Palma nana…), rimasero indietro alle nostre latitudini, nella lenta migrazione in tempi geologici delle piante dal Polo verso l’equatore. Segue la foto di Cristina di Smilax in fiore:
…e le foto delle foglie della Smilax mosse dal vento, di P. Pistoia
…. e la foto di alcune foglie dell’ “arbusteto” al P. San Domenico
——————————————————
DIGRESSIONE PER CORREGGERE LE IDEE CHE CREANO DEFAILLANCE
Seguiranno foto (anche di Cristina) e disegni schematici per il confronto con le altre due Oleacaee del genere Fillirea (F. angustifolia e latifolia) o Lillatro e con altre, con bacche e piccoli frutti, della macchia mediterranea.
Come nasce un’idea sbagliata?
Intanto la piantina della foto sotto è un Lillatro latifolia? Se sì, questa è la sola idea che avevamo del Lillatro. Non avevamo mai visto il Ligustro, nè il il Lillatro a foglia angusta, ne consegue……. una ‘ipotesi tentativa’ da falsificare. Se poi la risposta è negativa non avevamo mai visto nè un Lillatro nè un Ligustro, avevamo così ‘sparato’ una ‘ipotesi tentativa’ praticamente a caso (ipotesi debole), anche se per Popper, ipotesi scientificamente fondata.
Proponiamo due foto di un presunto Lillatro. Si tratta di un Lillatro a foglia larga? Come si presenta quello a foglia stretta?
I rametti riportati sotto sono dell’Oleacaea Fillirea latifolia?
———————————————–
Proponiamo a tempo debito agli autori del post in questa digressione una carrelata sulle piante della macchia mediterranea a piccoli frutti . Il percorso da seguire potrebbe essere quella accennato per l’Alisso; cioè scrivere un articolo con un Word Processor (da spedire per e-mail o da immettere direttamente dall’edit) con inserimento diretto al suo interno delle immagini (non verrebero inserite in .ipg, ma farebbero corpo con l’articolo, che verrebbe poi richiamato con un link da questo paragrafo. Sinceramente sono contrario a segmentare a mosaico (già la presenza del colore lo fa) le comunicazioni culturali, meglio una seriazione con indice! A mio avviso si perde in serietà, professionalità ed attenzione a favore del niente. (Vedere anche i testi scolastici attuali a mosaico pieni di macchie di colore e rimandi).
———————————————–
Una specie di ‘rapa’ a foglie larghe 2-3 sette verso il picciolo, a fiori gialli nata accanto alla Cerinthe al Ponso. A destra si intravede la grande rosetta di base riprese nella foto sotto.
Cristina, la nostra co-autrice e ‘classificatrice’ di riferimento, invitata ad osservare questa Crucifera, dalle foto è incerta fra una Brassica nigra (Senape nera) o Brassica rapa (Colza) se avesse le foglie abbraccianti il fusto, o ancora Rapistrum rugosum, se le piccole silique fossero meno allungate delle altre rotondeggenanti; dice che si recherà sul posto poi si vedrà.
Si è recata sul posto e racconta che:<< La fioritura della Brassicacea in questione sta diventando superba, come la rosetta di foglie che le sta vicino. Non è facile identificare questo genere di Brassicacee, tutte molto simili, soprattutto se la seconda loro fioritura non portasse ad osservare bene anche il frutto. Però vista da vicino, mi sono quasi convinta che si possa trattare di una Senape selvatica – Sinapis arvensis . Oltre il fiore, è proprio la rosetta basale che è tipica di questa pianta>>. Seguono le tre belle foto di Cristina di questa Senape:
Seguono anche tre foto di P. Pistoia delle foglie di Sinapsis arvensis
Silique e foglia superiore Sinapsis arvensis
Si allega la foto di una pagina ripresa da un interessante libro, con schizzi originali affiancanti lo scritto sintetico e rilevante, a firma di due ricercatrici dell’Istituto Botanico dell’ Università di Pisa, A.M. Pagni e G. Corsi, stampato da Arti Grafiche Pacini Mariotti, Pisa che ringraziamo.
——————————————-
SEGUONO FOTO DI CONFRONTO ATTUALE (metà ottobre) FRA: Erigeron (Conyza) bonariensis e Symphyotricum (=Aster) squamatum, ‘compagne’ sul campo, frequenti scendendo via dei Filosofi e verso Poggio Bianco a sinistra della strada.
Da riorganizzare e/o sostituire; è meglio ingrandire!
————————————————–
———————————————————–
Ecco la nuova piantina ‘puzzolente’ che sta crescendo; una Labiata (=Lamiacea) con foglie forse (se è affidabile il ricordo) simili in forma a quelle della Melissa profumata o delle mente selvatiche; è stata fotografata sul poggio del Ponso, vicino alle rosette di Cerinthe (le foglie sono di fatto più scure e risultano un po’ schiarite dal flasch).

Si notano i primi fiori di Labiata in basso a sinistra. Cristina Anna prima di pronunciarsi attende qualche fioritura più sostanziosa; oggi 31- Ottobre afferma: <<…suppongo si tratti di Ballotta nigra (Marrubio fetido) dato l’odore ed i fiori che stanno spuntando ora, anche se la vera fioritura è sicuramente a primavera; ho notato che l’infiorescenza che si nota nella tua foto, non si riferisce a questa pianta, bensì ad una Nepetella che si insinua sotto la pianta in questione>>. Si può osservare nell’ingrandimento o meglio attivandone il profumo ( nota dell’Estensore dello scritto). Seguono due foto di Cristina della Ballotta:
 Sembra che il nome della sottospecie della Ballotta si possa individuare dalla forma del calice; visionare il calice da P. Zangheri (op. cit.) della piantina Ballotta nigra subsp foetida (4156) e della Ballotta rupestris subsp foetida (4158)
Sembra che il nome della sottospecie della Ballotta si possa individuare dalla forma del calice; visionare il calice da P. Zangheri (op. cit.) della piantina Ballotta nigra subsp foetida (4156) e della Ballotta rupestris subsp foetida (4158)
Forse i lettori saprebbero, dalle foto di Cristina, ricavare la possibile sottospecie della Ballotta in questione!
————————————————————–
Oggi alla fine di Ottobre Cristina afferma “Comunque ho notato in questi ultimi periodi, sia le piante erbacee, sia gli arbusti e addirittura gli alberi da frutto, con le recenti situazioni meteorologiche un po’ estremizzate, hanno avuto una seconda fioritura se non addirittura anche una fruttificazione”
Oggi 31- Ottobre ho fotografato la Composita, Asteriscus, rinata che sta rifiorendo, insieme a vecchi capolini, andando verso San Vittore a sinistra subito dopo l’ultimo edificio della Villa di Campagna Sant’Anna; un altro Asteriscus e rinato in via dei Filosofi ad una ventina di metri dopo il bivio con via del Poderino scendendo a destra. Ho fotografato anche una nuova piantina ‘gracile’, ma invasiva in tutta la strada, da classificare:
———————————————————————–

Anche Cristina ha fotografata piantine come la precedente. <<Dal lato del Casale Ponsino fino ad oltre Sant’anna, si notano delle piantine di una Euphorbiacea con le foglioline seghettate color verde brillante, come pure la sua infiorescenza. Si dovrebbe chiamare Mercurialis annua (Mercorella comune)>>. Seguono le sue tre chiare foto:
NDC
Caratteristiche della Mercurialis annua: si notano piccoli fiori verdicci e insignificanti, unisessuali portati da piante separate (piante dioiche). I fiori maschili ridotti a un perianzio rudimentale, che circondano una decina di stami, sono raggruppati in glomeruli e aloro volta riuniti in spighe lasse. I fiori femminili anch’essi di scarsa rilevanza sono riuniti in gruppetti all’ascella delle foglie.
Ancora tre foto della Mercurialis a confronto 1 – con la Vetriola appena nata sull’argine poco prima del Ponsino, 2 – con la Lychnis alba (?) davanti alla strada del Ponsino e, poco dopo il Ponsino, 3 – con un’erbetta da classificare, vicino al cartello indicativo della Borrago, di P. Pistoia
FINE NDC
L’erbetta da classificare a destra potrebbe essere una Euphorbiacaea?
———————————————————————
Sempre Cristina nella sua visita del 31 ottobre afferma:<<Ancora poche decine di metri sotto Cherinte, ho notato delle piantine di Calendula, ma le foto non sono una meraviglia…>> Seguono tre foto della Calendula con capolini in fruttificazione.


Vorrei fare una riflessione. Calendula è un Genere appartenete alla famiglia delle Composite… è possibile, osservando le foto risalire alla specie? Ecco, ci si muove a costruire e comunicare l’ <idea> nella mente : “Il gatto è il gatto (Felino), perché ha i baffi a filo di ferro”. Sembra una battuta, ma è molto di più: è la risposta di un alunno (un po’ bernesco) a cui il docente ha tentato di insegnare nella classe l’idea del gatto! Se interpreto bene, mi sembra che le foto abbiano evidenziato i semi nel capolino e spesso i semi sono elementi classificatori importanti anche per la specie. Bisognerebbe sempre consapevolmente anche cercare di fotografare evidenziando quegli elementi che servono a chi osserva per costruire/comunicare l’idea della piantina in studio! Una foto specifica chiara dei semi della Calendula fotografata sopra potrebbe essere importante.
VISIONARE IL DISEGNO SCHEMATICO SEMI DI CALENDULA da S. Pignatti (op. cit)
C. officinalis: C, D, raramente b
C. arvensis: A, B, D
—————————————————————-
CRISTINA ANNA MORATTI termina la sua passeggiata sul nostro percorso floristico del mese di Ottobre, con queste osservazioni: <<Lungo tutto il percorso, è stato bello avere la compagnia della Bellis perennis. Questa piantina che fiorisce in ogni stagione, quando meno te lo aspetti, diventa anche prorompente, con i suoi capolini che decorano campi interi>>.
—————————————————–
SIAMO ARRIVATI A NOVEMBRE
Intanto non sono riuscito ad osservare i frutti della Calendola a qualche decina di metri dopo il Ponso. Comunque credo di non aver mai visto una Calendula!
Ho notato invece una crescita di pianticelle di Menta, anch’essa Labiata, non ancora fiorita, al bordo strada proprio davanti ai ciuffi della Ballotta nigra; qualche pianticella in fiore si trova invece a sinistra poco prima a circa un metro subito sotto strada. Le tre pianticelle, presenti insieme alla Ballotta, quattro se si aggiunge la Salvia selvatica, si distinguono nell’immediato strofinandole: la Ballotta è fetida, la Calaminta ‘sa’ di Nepitella e la Menta di Menta, la Salvia (?)… nessun odore! Ho cercato di fotografare come mi riesce:
Le foto sinottiche della piantina raccolta al Ponso è una Salvia selvatica?
La vegetazione così florida sul poggetto del Ponso è probabilmente favorita dal grosso accumulo di concime subito sotto strada.
————————————————-
Una ventina di metri dopo il Ponsino verso S. Vittore, sulla destra esiste una etichetta (ancora presente; quelle per la Cerinthe e per Achillea sono sparite!) per la Borago officinalis che era seccata; ora sono riapparse delle rosette di base; speriamo che siano di Borago ricresciuta.
——————————————————————————–
All’altezza del P. San Domenico, sul basso argine del podere dove da poco hanno piantato cipressetti toscani ‘affilati’, ho fotografato, una piantina che sta rifiorendo, con alcuni frutti verdastri a grappoli, rotondi di circa mezzo cm; all’aspetto e dal fiorellino mi è sembrata un erba Morella un po’ sciupata (i frutti della Morella, se ben ricordo, sono neri). Si richiedono approfondimenti.
—————————————————-
Oggi 4 Novembre nel tratto di via del poderino, subito sotto strada, vicino alla rete del campo sportivo, ho fatto fotografato una rosetta di Borragine rinata (?) e un’altra a foglie larghe da individuare, forse di una Lunaria annua o Medaglioni del Papa (Cristina).

Insieme alla rosetta di base a lamine ovate si notano: a sinistra in basso Il Chenopodium album fiorito (Farinaccio), La Mercurialis (Mercurella), tracce di erba di campo e in alto una specie di ”liana’ strisciante ….ed altro

Insieme alla rosetta forse di Borago officinalis (?), in basso di notano foglie di malva, a destra in alto si intravede la Mercurella e più al centro un ciuffo un po’ sbiadito di Ballota nigra (Marrubio fedido)…..ed altro

Probabile rosetta basale con foglie a cuore tendenzialmente triangolari astate forse di Lunaria annua o rediviva insieme in alto con la Mercurella circondata da una specie di ‘liana’ strisciante…ed altro. Se sviluppa vedremo.
Oggi 10 ott. ho posto un indicatore in lega di alluminio, a 4-5 metri dal secondo ingresso al P. Sant’Anna, sull’argine fra i cipressi, per indicare un mazzetto ancora in fiore (ancora per poco) di Galatelle (Aster linòrysis, Astro spilla d’oro). Intanto si è interrotta la discussione sulle piantine fotografate pochi giorni fa in via del Poderino, sotto strada vicino alla rete dello stadio: è stato rasato il prato sopra il campo sportivo! AD MAIORA.
DA SISTEMARE E DA CONTINUARE…..NELLA PARTE SECONDA




















































































































































































































































































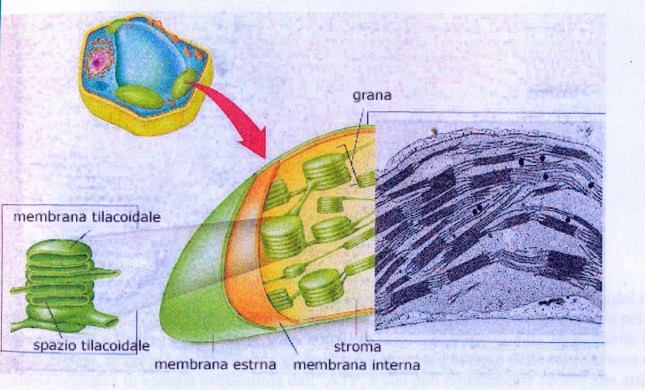
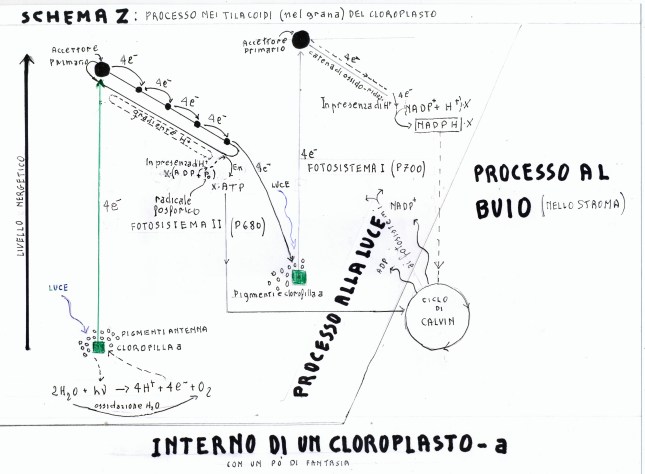
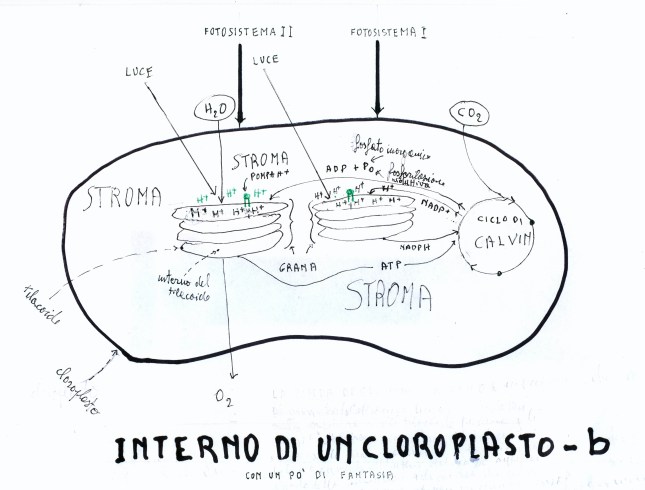
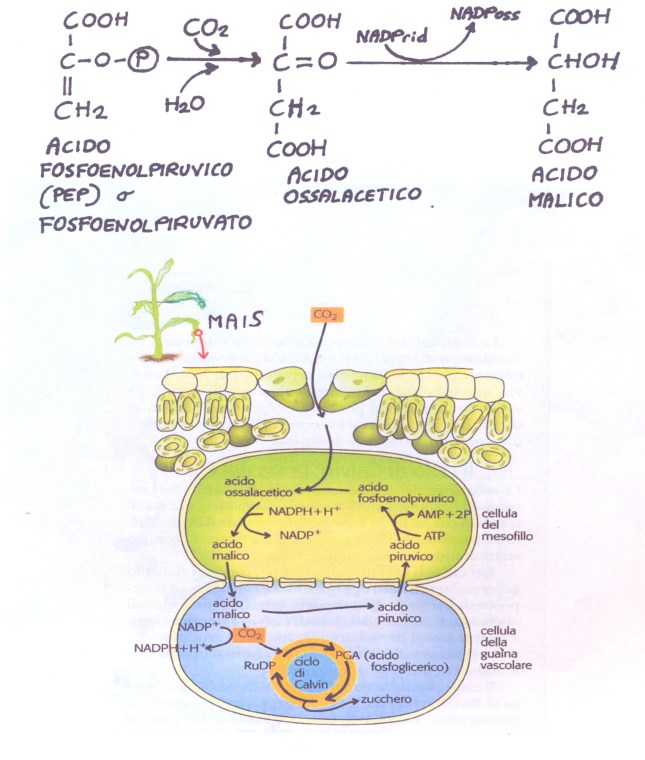
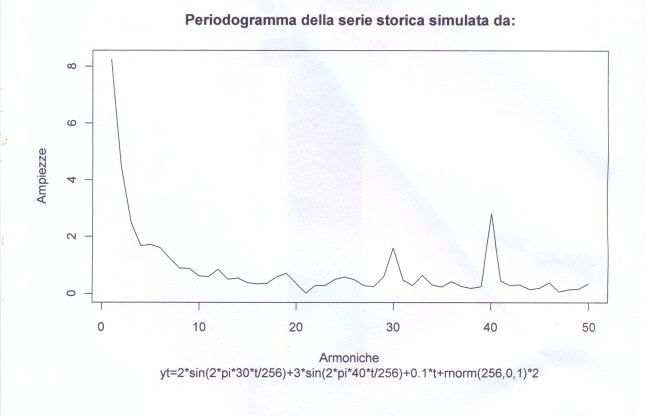
 ESERCIZIO N° 8
p
ESERCIZIO N° 8
p